Rút gọn biểu thức: A=[tex]\frac{\left ( 1^{4}+\frac{1}{4} \right )\left ( 3^{4}+\frac{1}{4} \right )\left ( 5^{4}+\frac{1}{4} \right )...\left ( 19^{4}+\frac{1}{4} \right )}{\left ( 2^{4}+\frac{1}{4} \right )\left ( 4^{4}+\frac{1}{4} \right )\left ( 6^{4}+\frac{1}{4} \right )...\left ( 20^{4}+\frac{1}{4} \right )}[/tex]
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
- 14 Tháng hai 2016
- 1,504
- 1,876
- 484
- Nghệ An
- $\color{Red}{\fbox{$\bigstar$ ĐHKTHC $\bigstar$}}$
Đặt [tex]\frac{2m+1}{m^{2}+2}[/tex] = a ta có: 2m+1 = am² + 2a (*)Chi minh voi cac ban : tim GTNN va GTLN cua B= (2m+1)/(m^2+2)
<=> am² - 2m + 2a - 1 = 0
pt có ∆' = 1 - a(2a - 1) = -2a² + a + 1 = -(2a + 1)(a -1)
Để phương trình (*) có nghiệm thì ∆' ≥ 0 => -(2a + 1)(a - 1) ≥ 0 => (2a + 1)(a - 1) ≤ 0
=> -1/2 ≤ a ≤ 1
Vậy min(a) = -1/2
max(a) = 1
Dấu bằng xảy ra <=>...
- 25 Tháng mười hai 2015
- 422
- 357
- 229
- 21
- Quảng Nam
- $\color{green}{\text{C-o-s-mos}}$
$\dfrac{\left ( 1^{4}+\dfrac{1}{4} \right )\left ( 3^{4}+\dfrac{1}{4} \right )\left ( 5^{4}+\dfrac{1}{4} \right )...\left ( 19^{4}+\dfrac{1}{4} \right )}{\left ( 2^{4}+\dfrac{1}{4} \right )\left ( 4^{4}+\dfrac{1}{4} \right )\left ( 6^{4}+\dfrac{1}{4} \right )...\left ( 20^{4}+\dfrac{1}{4} \right )}\\Rút gọn biểu thức A=[tex]\frac{\left ( 1^{4}+\frac{1}{4} \right )\left ( 3^{4}+\frac{1}{4} \right )\left ( 5^{4}+\frac{1}{4} \right )...\left ( 19^{4}+\frac{1}{4} \right )}{\left ( 2^{4}+\frac{1}{4} \right )\left ( 4^{4}+\frac{1}{4} \right )\left ( 6^{4}+\frac{1}{4} \right )...\left ( 20^{4}+\frac{1}{4} \right )}[/tex]
\\
= \dfrac{(1^2+\dfrac 1 2)^2-1^2}{(2^2+\dfrac 1 2)^2-2^2}.\dfrac{(3^2+\dfrac 1 2)^2-3^2}{(4^2+\dfrac 1 2)^2-4^2}...\dfrac{(19^2-\dfrac 1 2)^2-19^2}{(20^2-\dfrac 1 2)^2-20^2}\\
\\
=\dfrac{(1^2 -1+\dfrac1 2)(1^2+1+\dfrac 1 2)}{(2^2-2+\dfrac12)(2^2+2+\dfrac 1 2)}....\dfrac{(19^2-19-\dfrac 1 2)(19^2+19-\dfrac 1 2)}{(20^2-20-\dfrac 1 2)(20^2+20-\dfrac 1 2)}\\
\\
=.....$
Đến đây chỉ cần tính (đổi ra hỗn số) thì sẽ triệt tiêu được, nhanh gọn nhẹ =)))
- 28 Tháng hai 2017
- 4,472
- 5,490
- 779
- Hà Nội
- THPT Đồng Quan
a) hình như đề thiếu rồi bạn, $m$ bằng bao nhiêu mà chứng tỏ $m=3.(x^2+1)+x^2y^2+\dfrac{y^2}{(x+y)^2}+5$ bạn nhỉ?câu 1:
a) chứng tỏ m= 3.(x^2+1)+x^2y^2+y^-2/(x+y)^2+5
b) tìm số nguyên x,y biết 5/x+y/4=1/8
b) $\dfrac 5x=\dfrac y4=\dfrac18\Rightarrow \dfrac 5x=\dfrac18-\dfrac y4=\dfrac{1-2y}8\Rightarrow x=\dfrac{40}{1-2y}$
$x\in \mathbb{Z}\Rightarrow \dfrac{40}{1-2y}\in \mathbb{Z}\Rightarrow 1-2y\in Ư(40)$
Mà $1-2y$ là số lẻ $\Rightarrow 1-2y\in \left\{ \pm 1;\pm 5 \right\}\Rightarrow \cdots$
ừm thiếu bạn ạa) hình như đề thiếu rồi bạn, $m$ bằng bao nhiêu mà chứng tỏ $m=3.(x^2+1)+x^2y^2+\dfrac{y^2}{(x+y)^2}+5$ bạn nhỉ?
b) $\dfrac 5x=\dfrac y4=\dfrac18\Rightarrow \dfrac 5x=\dfrac18-\dfrac y4=\dfrac{1-2y}8\Rightarrow x=\dfrac{40}{1-2y}$
$x\in \mathbb{Z}\Rightarrow \dfrac{40}{1-2y}\in \mathbb{Z}\Rightarrow 1-2y\in Ư(40)$
Mà $1-2y$ là số lẻ $\Rightarrow 1-2y\in \left\{ \pm 1;\pm 5 \right\}\Rightarrow \cdots$
a) chứng tỏ m= 3.(x^2+1)+x^2y^2+y^-2/(x+y)^2+5 > 0 với mọi x thuộc Q
- 28 Tháng hai 2017
- 4,472
- 5,490
- 779
- Hà Nội
- THPT Đồng Quan
Ta có:ừm thiếu bạn ạ
a) chứng tỏ m= 3.(x^2+1)+x^2y^2+y^-2/(x+y)^2+5 > 0 với mọi x thuộc Q
$x^2\geq 0\Rightarrow x^2+1\geq 1\Rightarrow 3(x^2+1)\geq 3>0$
$x^2\geq 0;y^2\geq 0\Rightarrow x^2y^2\geq 0$
$y^2\geq 0;(x+y)^2+5>0\Rightarrow \dfrac{y^2}{(x+y)^2+5}\geq 0$
$\Rightarrow 3(x^2+1)+x^2y^2+\dfrac{y^2}{(x+y)^2+5}>0$ hay $m>0$
Giải một câu PTTNT, câu b tương tự, ai giải xem nhé:
a. $(x^2-3x+2)^2-4x+2=(x^2-3x+2)^2-x^2+x^2-4x+2$
bạn có thể giải thích cho mình cái mình gạch đc không mk không hiểu chỗ đấy lắm
$=(x^2+3x+2+x)(x^2-3x+2-x)+(x^2-4x+2)$
$=(x^2-4x+2)(x^2-2x+2+1)=(x^2-4x+2)(x^2-2x+3)$
phân tích đa thức sau thành nhân tử:
a)x^3-x^2y+3x-3y
b)x^3-2x^2-4xy^2+x
c)(x+2)(x+3)(x+4)(x+5)-8
a)x^3-x^2y+3x-3y
b)x^3-2x^2-4xy^2+x
c)(x+2)(x+3)(x+4)(x+5)-8
a, [tex]x^{3}-x^{2}y+3x-3y=x^{2}(x-y)+3(x-y)=(x^{2}+3)(x-y)[/tex]phân tích đa thức sau thành nhân tử:
a)x^3-x^2y+3x-3y
b)x^3-2x^2-4xy^2+x
c)(x+2)(x+3)(x+4)(x+5)-8
b, [tex]x^{3}-2x^{2}-4xy^{2}+x=x(x^{2}-2x-4y^{2}+1)=x[x(x-1-2y)-(x-1-2y)+2y(x-1-2y)]=x(x-1+2y)(x-1-2y)[/tex]
c, [tex](x+2)(x+3)(x+4)(x+5)-8=(x^{2}+7x+10)(x^{2}+7x+12)-8[/tex] (*)
Đặt [tex]x^{2}+7x+11=a[/tex]
Khi đó (*) có dạng [tex](a-1)(a+1)-8=a^{2}-9=(a-3)(a+3)[/tex]
Trở lại cách đặt
[tex](x^{2}+7x+11-3)(x^{2}+7x+11+3)=(x^{2}+7x+8)(x^{2}+7x+14)=(2x+7-\sqrt{17})(2x+7+\sqrt{17})[/tex]
- 23 Tháng sáu 2017
- 691
- 1,103
- 189
- 23
- Bà Rịa - Vũng Tàu
- Taylors College
d)cm
a)8 99...99 (2008 c/s 9) la hop so
b) x(x-a)(x+a)(x+2a)là bình phương 1 đa thức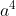
c)xy+1 là số chính phương biết x=11..115(n c/s 1), y=1...19(n c/s 1)
d)cho a+b+c=1 và. C/m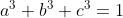
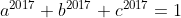
- 16 Tháng mười hai 2017
- 1
- 0
- 1
- 22
- TP Hồ Chí Minh
- THPT chuyên Trần Đại Nghĩa
Các bạn giúp mình bài này với:
Dùng đồng dư thức để chứng minh (300^3000 - 1) chia hết cho 1001?
Dùng đồng dư thức để chứng minh (300^3000 - 1) chia hết cho 1001?
- 6 Tháng tám 2017
- 592
- 263
- 134
- 21
- Phú Yên
- THCS Huỳnh Thúc Kháng
[tex]a)(x+1)(x+4).(x+2)(x+3)-3=(x^{2}+5x+4)(x^{2}+5x+6)-3[/tex]Phân tích đa thức thành nhân tử
a)(x+1)(x+2)(x+3)(x+4) - 3
b)(a+b+c)(ab+bc+ca)-abc
c)a^3+b^3+c^3-3abc
d)a*(b+c)^2(b-c)+b(c+a)^2(c-a)+c(a+b)^2(a-b)
Đặt [tex]x^{2}+5x+4[/tex]=a
Ta có [tex]a(a+2)-3=a^{2}+2a-3[/tex]
=[tex]a^{2}+3a-a-3[/tex]
=[tex]a(a+3)-(a+3)[/tex]
=(a+3)(a-1)
=[tex](x^{2}+5x+7)(x^{2}+5x+3)[/tex]
b)(a+b+c)(ab+bc+ca)-abc
=[tex]a^{2}b+a^{2}c+abc+ab^{2}+b^{2}c+abc+abc+bc^{2}+ac^{2}-abc[/tex]
=[tex](abc+a^{2}b)+(abc+bc^{2})+(ab^{2}+b^{2}c)+(ac^{2}+a^{2}c)[/tex]
=[tex]ab(a+c)+bc(b+c)+b^{2}(a+c)+ac(a+c)[/tex]
=[tex](a+c)(ab+bc+ca+b^{2})[/tex]
=[tex](a+c)[(ab+b^{2})+(ac+bc)][/tex]
=(a+b)(b+c)(c+a)
c)a^3+b^3+c^3-3abc
=[tex](a+b)^{3}-3ab(a+b)+c^{3}-3abc[/tex]
=[tex](a+b)^{3}-3a^{2}b-3ab^{2}+c^{3}-3abc[/tex]
=[tex][(a+b)^{3}+c^{3}]-(3a^{2}b+3ab^{2}+3abc)[/tex]
=[tex](a+b+c)[(a+b)^{2}-c(a+b)+c^{2}]-3ab(a+b+c)[/tex]
=[tex](a+b+c)(a^{2}+2ab+b^{2}-ca-cb+c^{2}-3ba)[/tex]
=[tex](a+b+c)(a^{2}+b^{2}+c^{2}-ab-bc-ca)[/tex]
d)a*(b+c)^2(b-c)+b(c+a)^2(c-a)+c(a+b)^2(a-b)= (a - b)(b - c)(c - a)(a + b + c)
Đánh mỏi tay quá!Câu d đành ghi luôn đáp số vậy.Xin bạn thông cảm.r36
Vậy a-b =0 thì sao bạnđể mình mở đầu trước cho nào!!!!!!
Câu 1:
$a^2(b+c)$=$b^2(c+a)$
\Rightarrow $a^2b+a^2c$-$b^2c$-$b^2a$=0
\Rightarrow $ab.(a-b)$+$c.(a-b).(a+b)$=0
\Rightarrow $(ab+ac+bc).(a-b)$=0
vậy $(ab+ac+bc)$=0
\Rightarrow $(ab+ac+bc).(b-c)$=0
\Rightarrow $b^2a+b^2c-c^2b-c^2a$=0
\Rightarrow $b^2(c+a)=c^2(a+b)$
mọi người giúp e bài bày với ạ ! Cảm ơn !!!
[tex]Cho x,y,z dương và x+y+z=1. Chứng minh: \frac{1}{x^2+2yz}+\frac{1}{y^2+2xz}+\frac{1}{z^2+2xy} \geq 9[/tex]
[tex]Cho x,y,z dương và x+y+z=1. Chứng minh: \frac{1}{x^2+2yz}+\frac{1}{y^2+2xz}+\frac{1}{z^2+2xy} \geq 9[/tex]



