- 6 Tháng tám 2017
- 592
- 263
- 134
- 20
- Phú Yên
- THCS Huỳnh Thúc Kháng
Viết lại đề [tex]\frac{x-3}{2017}+\frac{x-4}{2016}+\frac{x-5}{2015}+\frac{x-6}{2014}=4[/tex]
[tex]\Leftrightarrow \left ( \frac{x-3}{2017}-1 \right )+\left ( \frac{x-4}{2016}-1 \right )+\left ( \frac{x-5}{2015} -1\right )+\left ( \frac{x-6}{2014}-1 \right )=0[/tex]
[tex]\Leftrightarrow \frac{x-2020}{2017}+\frac{x-2020}{2016}+\frac{x-2020}{2015}+\frac{x-2020}{2014}=0[/tex]
[tex]\Leftrightarrow \left ( x-2020 \right )\left ( \frac{1}{2017}+\frac{1}{2016}+\frac{1}{2015}+\frac{1}{2014} \right )=0[/tex]
[tex]\Leftrightarrow x-2020=0[/tex] ([tex]\left ( \frac{1}{2017}+\frac{1}{2016}+\frac{1}{2015}+\frac{1}{2014} \right )>0[/tex]
[tex]\Leftrightarrow x=2020[/tex]
- 17 Tháng sáu 2016
- 104
- 128
- 106
- 21
- Quảng Ngãi
- Trường THPT chuyên Lê Khiết
Trừ từng vế 2 pt đc: [tex]a^{2}(1-a)+b^{2}(1-b)+c^{2}(1-c)=0[/tex] (1)chotinh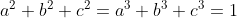
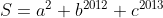
Ta sẽ cm 1-a, 1-b, 1-c đều không âm. Thật vậy, giả sử 1-a<0 thì a>1 nên [tex]a^{2}[/tex] >1 suy ra [tex]a^{2}+b^{2}+c^{2}> 1[/tex], trái với [tex]a^{2}+b^{2}+c^{2}= 1[/tex].
Do 1-a, 1-b, 1-c không âm nên từ (1) suy ra
[tex]a^{2}(1-a)=b^{2}(1-b)=c^{2}(1-c)=0[/tex]
Do đó mỗi số x,y,z hoặc bằng 0 hoặc bằng 1
Loai TH ba số bằng 0, ba số bằng 1; hai số bằng 1 và 1 số bằng 0
Vậy trong ba số a,b,c có hai số bằng 0, một số bằng 1
=>[tex]a^{2}+b^{2012}+c^{2013}=1[/tex]
- 6 Tháng tám 2017
- 592
- 263
- 134
- 20
- Phú Yên
- THCS Huỳnh Thúc Kháng
Xét delta ~~tim cap x, y nguyen thoa man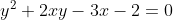
$\Delta = 4x^2+12x+8=(2x+3)^2-1\geq 0 \Leftrightarrow x\geq -1 ,,,,,x\leq -2$
BĐT cần chứng minh $\Leftrightarrow \frac{1}{1+x^{2}}+\frac{1}{1+y^{2}}-\frac{2}{1+xy}\geq 0$cho x, y thoa man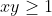
chung minh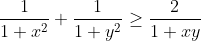
$\Leftrightarrow \frac{(1+y^{2})(1+xy)+(1+x^{2})(1+xy)-2(1+y^{2})(1+x^{2})}{(1+xy)(1+y^{2})(1+x^{2})}\geq 0$
$\Leftrightarrow \frac{1+xy+y^{2}+xy^{3}+1+xy+x^{2}+x^{3}y-2-2x^{2}-2y^{2}-2x^{2}y^{2}}{(1+xy)(1+y^{2})(1+x^{2})}\geq 0$
$\Leftrightarrow \frac{2xy+x^{3}y+xy^{3}-x^{2}-y^{2}-2x^{2}y^{2}}{(1+xy)(1+y^{2})(1+x^{2})}\geq 0$
$\Leftrightarrow \frac{xy(x^{2}+y^{2}-2xy)-(x^{2}-2xy+y^{2})}{(1+xy)(1+y^{2})(1+x^{2})}\geq 0$
$\Leftrightarrow \frac{(xy-1)(x-y)^{2}}{(1+xy)(1+y^{2})(1+x^{2})}\geq 0 $ luôn đúng vì [tex]xy\geq 1[/tex]
- 6 Tháng tám 2017
- 592
- 263
- 134
- 20
- Phú Yên
- THCS Huỳnh Thúc Kháng
Ta cóchung minh voi moi n>=0
chia het cho 91-6^{n}(3^{n}+2^{n}))
[tex]=(25^{n}-18^{n})-(12^{n}-5^{n})[/tex]
[tex]=(25-18)\left [25^{n-1}+25^{n-2}.18+...+18^{n-1} \right ]-\left ( 12-5 \right )\left [ 12^{n-1}+12^{n-2}.5+...+5^{n-1} \right ][/tex]
[tex]=7\left [25^{n-1}+25^{n-2}.18+...+18^{n-1}+12^{n-1}+12^{n-2}.5+...+5^{n-1} \right ][/tex] chia hết cho 7
Lại có
[tex]=(25^{n}-12^{n})-(18^{n}-5^{n})[/tex]
[tex]=(25-12)\left [25^{n-1}+25^{n-2}.12+...+12^{n-1} \right ]-\left ( 18-5 \right )\left [ 18^{n-1}+18^{n-2}.5+...+5^{n-1} \right ][/tex]
[tex]=13\left [25^{n-1}+25^{n-2}.12+...+12^{n-1}+18^{n-1}+18^{n-2}.5+...+5^{n-1} \right ][/tex] chia hết cho 13
Mà (7;13)=1 nên
- 6 Tháng tám 2017
- 592
- 263
- 134
- 20
- Phú Yên
- THCS Huỳnh Thúc Kháng
Giải bpt 1:tim x nguyen thoa man 2 bat phuong trinh sau:
(1) (cho x0,8 co nghia la nhan voi 0,8)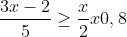
va
(2)
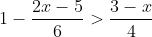
[tex]\Leftrightarrow \frac{3x-2}{5}\geq \frac{2}{5}[/tex]
[tex]\Leftrightarrow 3x-2\geq 2[/tex]
[tex]\Leftrightarrow x\geq \frac{4}{3}[/tex]
Giải bpt 2:
[tex]\Leftrightarrow 12-4x+15\geq 9-3x[/tex]
[tex]\Leftrightarrow -3x+4x\leq 12+15-9[/tex]
[tex]\Leftrightarrow x\leq 18[/tex]
Vì x phải là số nguyên nên x thỏa mãn 2 bpt trên là [tex]2\leq x\leq 18[/tex]
- 27 Tháng mười 2017
- 4,573
- 7,825
- 774
- 21
- Hà Nội
- Trường Đời
T=2/(2-1) + (1-a)/(1+a)
chô bôi đên sai sai thì phải bạn ơi
coi lại giùm mình
phải là a - 1 chứ ạ?