N
N
nhockthongay_girlkute
[TEX]\left{[x+2]^2+[y+3]^2= -[y+3][x+z-2]\\{x^2+5x+9z-7y-15=-3yz\\{8x^2+18y^2+18xy+18yz= -84x-72y-24z-176[/TEX]
N
nhockthongay_girlkute
N
nhockthongay_girlkute
P
puu
1 \Leftrightarrow[TEX]2x=(\sqrt{2}-x).\sqrt{x^2+2}[/TEX]
\Leftrightarrow[TEX]\left{\begin{x(\sqrt{2}-x)\geq 0}\\{4x^2=(x^2-2\sqrt{2}x+2)(x^2+2)[/TEX]
\Leftrightarrow[TEX]\left{\begin{0 \leq x \leq \sqrt{2}}\\{x^4+4-2\sqrt{2}x(x^2+2)=0[/TEX]
\Leftrightarrow[TEX]\left{0 \leq x \leq \sqrt{2}}\\{(x^2+2-\sqrt{2}x)^2-6x^2=0[/TEX]
các bạn làm thêm bài này nhá
[TEX]\left{\begin{x^3+4y=y^3+16x}\\{1+y^2=5(1+x^2)}[/TEX]
Last edited by a moderator:
H
haruka18
Giải hệ pt:
[tex]\left{(x-1).\sqrt{y}+(y-1)\sqrt{x}=\sqrt{2xy} \\ x \sqrt{y-1}+y \sqrt{x-1}=xy[/tex]
[tex]\left{(x-1).\sqrt{y}+(y-1)\sqrt{x}=\sqrt{2xy} \\ x \sqrt{y-1}+y \sqrt{x-1}=xy[/tex]
N
nhockthongay_girlkute
để ý phương trình (2)
có
[TEX] x\sqrt{y-1} \leq \frac{xy}{2} [/TEX]
[TEX] y\sqrt{x-1} \leq \frac{xy}{2} [/TEX]
=> dấu "=" xảy ra
x=y=2
chẳng biết đúng hay sai :-SS
P
puu
2. vì y khác 0 nên chia cả 2 vế của PT (2) cho y ta có
[TEX]\frac{x}{y}+\frac{1}{\sqrt{x^2+1}+x}+x=0[/TEX]
\Leftrightarrow[TEX]\frac{x}{y}+\sqrt{x^2+1}-x+x=0[/TEX]
\Leftrightarrow[TEX]\frac{x}{y}=-\sqrt{x^2+1}[/TEX]
\Leftrightarrow[TEX]\left{\begin{xy<0}\\{\frac{x^2}{y^2}=x^2+1[/TEX]
thay vào PT (1) đến đây dễ rồi nhỉ
Last edited by a moderator:
H
herrycuong_boy94
Q
quyenuy0241
Giải phương trình sau bằng phương pháp lượng giác:
(1)
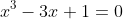
[tex]VT=f(x)[/tex], dễ thấy hàm số [tex]f(x)[/tex] liên tục trên [tex]R[/tex]
rõ ràng PT có 3 nghiệm thuộc khoảng [tex][-2,2] [/tex] thật vậy:
[tex]f(-2).f(0)<0 \\ f(0).f(1)<0 \\ f(1).f(2)<0 [/tex]
Đặt [tex] x=2cosA [/tex]
[tex]PT(1) [/tex] trở thành:
[tex]8cos^3A-6cosx+1=0 \Leftrightarrow cos3A=\frac{-1}{2} [/tex]
Do tính tuần hoàn ta chỉ cần xét [tex]A \in [\frac{- \pi}{2}, \frac{\pi}{2} [/tex]]....
.......
0
01263812493
Ghpt:
[TEX]\left{a+b+c=3\\ab=-2\\b^2+c^2=1[/TEX]
Gpt
[TEX]\sqrt[4]{1-x}+\sqrt[4]{2-x}=\sqrt[4]{3-2x}[/TEX]
D
duynhan1
Ghpt:
[TEX]\left{a+b+c=3\\ab=-2\\b^2+c^2=1[/TEX]
Gpt
[TEX]\sqrt[4]{1-x}+\sqrt[4]{2-x}=\sqrt[4]{3-2x}[/TEX]
1)
Thế [TEX]c = 3 -a -b [/TEX] vào 3 kết hợp với 2 ta có hệ đơn giản để giải
2)
[TEX]\left{ a^4 - b^4 = 1 \\ (a + b)^4 = a^4 + b^4 [/TEX]
[TEX]\Leftrightarrow \left{ a^4 - b^4 = 1 \\ 4ab(a^2+b^2) + 6a^2b^2 = 0 [/TEX] :-\"
T
tell_me_goobye
0
01263812493
1)
Thế [TEX]c = 3 -a -b [/TEX] vào 3 kết hợp với 2 ta có hệ đơn giản để giải
Em thế vào (3)
[TEX]b^2+(3-a-b)^2=2b^2+a^2-6b-6a+4=0[/TEX]
Nhưng đến đây sao a
[TEX]\Leftrightarrow \left{(x-2)(x+1)^2=2-y\\(y-2)(y+1)^2=2-z\\(z-2)(z+1)^2=2-x[/TEX]
Last edited by a moderator:
N
nhockthongay_girlkute
Em thế vào (3)
[TEX]b^2+(3-a-b)^2=2b^2+a^2-6b-6a+4=0[/TEX]
Nhưng đến đây sao a
thay tiếp [TEX] a=\frac{-2}{b} [/TEX] ok
0
01263812493
Em thế vào (3)
[TEX]b^2+(3-a-b)^2=2b^2+a^2-6b-6a+4=0[/TEX]
Nhưng đến đây sao a
thay tiếp [TEX] a=\frac{-2}{b} [/TEX] ok
[TEX]\Leftrightarrow b^4-3b^3+2b^2+6b+2=0[/TEX]
======================================
Last edited by a moderator:
L
legendismine
0
01263812493
[TEX]\left{x+y=a\\xy=b[/TEX]
Có lẽ bài toán thành tìm nguyện nguyên của pt: [TEX]a^3-3ab+2b=54[/TEX]
T