[Chuyên đề 2] Phương trình, hệ phương trình

[tell_me_goobye]

[TEX]x^3=4x+1[/TEX]
Giải hộ em bằng công thứ c Cardano ạ

 

[ngomaithuy93]

[TEX]GHPT: \left{|xy-18|=12-x^2(1)\\{xy=9+\frac{1}{3} y^2(2)[/TEX]

[TEX](2): \Leftrightarrow \frac{1}{3}y^2-xy+9=0[/TEX]

[TEX]\Delta =x^2-12 \leq 0 (theo (1)[/TEX]
[TEX]\Rightarrow \left{{x^2-12=0}\\{xy=9+\frac{1}{3}y^2}[/TEX]

 

[duynhan1]

[TEX]x^3=4x+1[/TEX]
Giải hộ em bằng công thứ c Cardano ạ

[TEX]\Leftrightarrow x^3 - 4x - 1 = 0 [/TEX]

[TEX]\Delta = b^2 - 3ac = 12 [/TEX]

[TEX]k = \frac{ - 27 a^2 d }{2\sqrt{\Delta^3}} = \frac{9 }{16\sqrt{3}}<1 [/TEX]

[TEX]k<1 \Rightarrow [/TEX]Có 3 nghiệm :

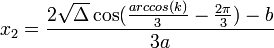
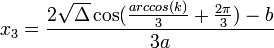
Hic hic giải mãi mà ko nhớ CT =((

 

[tell_me_goobye]

[TEX]\left{x^2+y^2+1=2x+2y\\{[2x-y-2]y=1}[/TEX]

[TEX]HPT\Leftrightarrow\left{(x-1)^2+(y-1)^2=1\\{(2x-y-2)y=1[/TEX]
[TEX]PT 2\Leftrightarrow2xy-y^2-2y-1=0[/TEX]
\Leftrightarrow[TEX]y^2+2y(1-x)^2+1=0[/TEX]
để hệ có nghiệm thi` [TEX]\triangle\ =[1-x]^2-1 \ge\ 0[/TEX]
\Leftrightarrow[TEX][1-x]^2 \ge\ 1[/TEX]
mà từ PT \Rightarrow[TEX][x-1]^2\le\ 1[/TEX]
\Rightarrow [TEX][x-1]^2=1[/TEX]
\Rightarrow x;y

 

[tell_me_goobye]

[TEX]\left{x^4-y^4=240\\{x^3-2y^3=3[x^2-4y^2]-4[x-8y][/TEX]

:-*:-*:-*:-*

hệ viết lại như sau

[TEX]\left{\begin{ x^4=y^4+240(1)}\\{x^3-3x^2+4x=2y^3-12y^2+32y(2)} [/TEX]

nhân 2 vế của (2) với (-8) rồi cộng với 2 vế của (1) ta có

[TEX](x-2)^4=(y-4)^4 <=> \left[\begin{x-2=y-4}\\{x-2=4-y} [/TEX]

đến đây các bạn tự giải tiếp !

 

[tell_me_goobye]

giải hệ sau

[TEX] \left{\begin{6x^2y+2y^3+35=0}\\{5x^2+5y^2+2xy+5x+13y=0}[/TEX]

 

[tell_me_goobye]

giải hệ

[TEX] \left{\begin{\frac{4z^2}{1+4z^2}=x}\\{\frac{4x^2}{1+4x^2}=y}\\{\frac{4y^2}{1+4y^2}=z}[/TEX]

 

[tell_me_goobye]

giải hệ

[TEX] \left{\begin{xyz=8}\\{x^2y+y^2z+z^2x=73}\\{x(y-z)^2+y(z-x)^2+z(x-y)^2=98}[/TEX]

 

[tell_me_goobye]

giải phương trình

[TEX] \frac{3x^4+9x^3+17x^2+11x+8}{3x^2+4x+5}=(x+1)\sqrt{x^2+3}[/TEX]

 

[bigbang195]

giải hệ

[TEX] \left{\begin{xyz=8}\\{x^2y+y^2z+z^2x=73}\\{x(y-z)^2+y(z-x)^2+z(x-y)^2=98}[/TEX]

 

[bigbang195]

giải hệ

[TEX] \left{\begin{\frac{4z^2}{1+4z^2}=x}\\{\frac{4x^2}{1+4x^2}=y}\\{\frac{4y^2}{1+4y^2}=z}[/TEX]

dễ thấy [TEX]x,y,z>0[/TEX]

Dùng AM-GM cho mẫu ta có[TEX] x=y=z[/TEX] .

 

[chuanho]

gui

[TEX]\Leftrightarrow b^4-3b^3+2b^2+6b+2=0[/TEX]
======================================

bạn ko cần thay vào như thế đâu bạn triển khai cái này [TEX](3-a-b)^2[/TEX] ra rui triệt tiêu xong chỉ còn : ab=-5 thui kết hợp với 2 \Rightarrowpt vô n OK nha

 

[chuanho]

hệ pt

mọi người cùng làm nha :

[TEX]\left{\begin{\sqrt{x}+\sqrt{y}=5\\\sqrt{x+5}+\sqrt{y+5}=8}[/TEX]​

2/

[TEX]\left{\begin{\sqrt{x}+\sqrt{2-x}=\sqrt{2}\\{\sqrt{2-x}+\sqrt{y}=\sqrt{2}[/TEX]​

3/

[TEX]\left{\begin{x+y+z=-2\\x^2+y^2+z^2=6\\x^3+y^3+z^3=-6\\z\geq 1 [/TEX]​

4/

[TEX]\left{\begin{x+y+z=6\\xy+yz-zx=7\\x^2+y^2+z^2=14[/TEX]​

5/

[TEX]\left{\begin{x+y+\frac{1}{x}+\frac{1}{y}=4\\{x^2+y^2+\frac{1}{x^2}+\frac{1}{y^2}[/TEX]​

6/

[TEX]\left{\begin{x+y=5\\x^4+y^4=97}[/TEX]​

7/

[TEX]\left{\begin{xy=3\\x^4+y^4=82[/TEX]​

8/

[TEX]\left{\begin{(\frac{x}{y})^2)+(\frac{x}{y})^3=12\\{(xy)^2+xy=6}[/TEX]​

9/

[TEX]\left{\begin{x+y-\sqrt{xy}=3\\{\sqrt{x+1}+\sqrt{y+1}=4[/TEX]​

10/

[TEX]\left{\begin{x^3-8x=y^3+2y\\x^2-3=3(y^2+1)[/TEX]​

11/

[TEX]\left{\begin{x^2-xy+y^2=3(x-y)\\{x^2+xy+y^2=7(x-y)^3 (vsx,y thuộc R)[/TEX]​

12/

[TEX]\left{\begin{xy+x+1=7y\\{x^2y^2+xy+1=13y^2[/TEX]​

13/

[TEX]\left{\begin{x^4-x^3y+x^2y^2=1\\{x^3y-x^2+xy=-1[/TEX]​

14/

[TEX]\left{\begin{y+xy^2=6x^2\\{1+x^2y^2=5x^2[/TEX]​

15/

[TEX]\left{\begin{(x-y)(x^2+y^2)=13\\{(x+y)(x^2-y^2)=25[/TEX]
các bạn hãy cùng trổ tài đi nha! @};-@};-@};-​

 

[duynhan1]

bạn ko cần thay vào như thế đâu bạn triển khai cái này [TEX](3-a-b)^2[/TEX] ra rui triệt tiêu xong chỉ còn : ab=-5 thui kết hợp với 2 \Rightarrowpt vô n OK nha

Sao triệt tiêu được vậy.

mọi người cùng làm nha :

[TEX]\left{\begin{\sqrt{x}+\sqrt{y}=5\\\sqrt{x+5}+\sqrt{y+5}=8}[/TEX]​

2/

[TEX]\left{\begin{\sqrt{x}+\sqrt{2-x}=\sqrt{2}\\{\sqrt{2-x}+\sqrt{y}=\sqrt{2}[/TEX]​

Cộng trừ rồi nhân liên hiệp đặt ẩn phụ ta có hệ có dạng :

[TEX]\left{ a+b = ... \\ \frac{1}{a} + \frac{1}{b} = ...[/TEX]

 

[duynhan1]

4/

[TEX]\left{\begin{x+y+z=6\\xy+yz-zx=7\\x^2+y^2+z^2=14[/TEX]​

Nhân 2 cho 2 rồi lấy (3)-(2) ta có :

[TEX](x+z-y)^2 = 0 [/TEX]

5/

[TEX]\left{\begin{x+y+\frac{1}{x}+\frac{1}{y}=4\\{x^2+y^2+\frac{1}{x^2}+\frac{1}{y^2}[/TEX]​

đặt :

[TEX] \left{ a = x + \frac{1}{x} \\ b = y + \frac{1}{y} [/TEX]

6/

[TEX]\left{\begin{x+y=5\\x^4+y^4=97}[/TEX]​

Thế (1) vào (2) được phương trình bậc 4 và ta có 2 nghiệm 2 và 3 nên hạ xuống bậc 2 dễ dàng bằng Hoocne

7/

[TEX]\left{\begin{xy=3\\x^4+y^4=82[/TEX]​

[TEX]x^4 + y^4 = (x^2 + y^2)^2 - 18 \Rightarrow x^2 + y^2 = 10 [/TEX]

 

[duynhan1]

8/

[TEX]\left{\begin{(\frac{x}{y})^2)+(\frac{x}{y})^3=12\\{(xy)^2+xy=6}[/TEX]​

Từ (1) [TEX]\Rightarrow x=2y [/TEX]

9/

[TEX]\left{\begin{x+y-\sqrt{xy}=3\\{\sqrt{x+1}+\sqrt{y+1}=4[/TEX]​

Bình phương (2) rồi đặt [TEX]\left{ S= x+y\\ P =xy[/TEX]

 

[duynhan1]

11/

[TEX]\left{\begin{x^2-xy+y^2=3(x-y)\\{x^2+xy+y^2=7(x-y)^3 (vsx,y \in R)[/TEX]​

15/

[TEX]\left{\begin{(x-y)(x^2+y^2)=13\\{(x+y)(x^2-y^2)=25[/TEX]
các bạn hãy cùng trổ tài đi nha! @};-@};-@};-​

Nhân chép đưa về đồng bậc

Bài 11 còn 1 cách nữa đó là đặt

S=x-y
P=xy

cái này cậu giải ra đi để tớ xem ha hi hi năn nỉ đấy giúp đi nha!

Tớ sẽ giải cách đưa về đồng bậc cho bài 15 :

Nhân chéo ta có :

[TEX]\left[ x-y = 0 (loai) \\ 25(x^2+y^2) = 13 (x+y)^2 [/TEX] Dễ dàng giải tiếp

Còn bài 11 nên làm theo cách 2 8-}

Sức mình có hạn xử mấy bài dễ. Mấy bài khó để lại :">

 

[chuanho]

hoi

Nhân chép đưa về đồng bậc .

cái này cậu giải ra đi để tớ xem ha hi hi năn nỉ đấy giúp đi nha!

 

[01263812493]

Ngu vs bài này
[TEX]\left{xy^2-2y+3x^2=0\\y^2+x^2y+2x=0[/TEX]

 

[cool_strawberry]

Ngu vs bài này
[TEX]\left{xy^2-2y+3x^2=0\\y^2+x^2y+2x=0[/TEX]

TH1: x=0 \Rightarrow y=0
TH2: x #0
Nhân 2 vế của pt 2 vs x rồi trừ theo vế cho pt1 được:
[TEX]x^3y+2y-x^2=0[/TEX]
Tính y theo x rồi thay vào pt.

Pt bậc cao nhưng chắc sẽ giải đc (chưa nháp)