Q
quyenuy0241
[tex]2\sqrt{\frac{1}{3}a}.\sqrt{ab} \le \frac{a}{3}+ab[/tex]................Cho các số thực dương. thỏa mãn Chứng minh
Chứng minh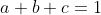
rằng :

Last edited by a moderator:
[tex]2\sqrt{\frac{1}{3}a}.\sqrt{ab} \le \frac{a}{3}+ab[/tex]................Cho các số thực dương. thỏa mãn Chứng minh
Chứng minh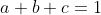
rằng :

[tex]\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3} \ge \frac{3}{abc}[/tex]Cho các số thực dương. Chứng minh rằng :

[tex]\frac{b}{a^2}+\frac{1}{b} \ge \frac{2}{a}[/tex]Cho các số thực dương. Chứng minh rằng :

Tìm giá trị lớn nhất của biểu thức:
[TEX]\frac{2004x^2+6006x+6\sqrt{x^3-2x^2+x-2}-8003}{x^2+3x+4}[/TEX]
Cho các số thực dương. thỏa mãn Chứng minh rằng :
Chứng minh rằng :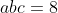

Mọi người cố gắng làm hết nhé
p/s: Spam cho lên bài nhanh =))
Cho các số thực dương. Chứng minh rằng :

[tex]Do--> a,b,c>0...and... a+b+c=1 \Rightarrow a,b,c<1[/tex]Cho các số thực dương. thỏa mãn Chứng minh
Chứng minh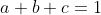
rằng :

Làm thử coi!!!
Giống bài của anh vodichhocmai :
nhưng lại dễ hơn
[tex]\sum{\frac{a}{a+b^4+c^4}} \le 1 [/tex] Với [tex]a,b,c >0 ............abc=1[/tex]
[tex]\sum{\frac{a}{a+b^n+c^n} \le 1 \ \ n\ge 1[/tex]
Đề bài 1 đúng ko? ......................................
Đề đúng, hok sai|.
Bài nữa : Cho a\geq3;b\geq4;c\geq2. Tìm max :>-
[TEX] A = \frac{ab \sqrt{c-2} + bc\sqrt{a-3} + ac\sqrt{b-4}}{abc} [/TEX]
[TEX]\sum\frac{a^2}{\sqrt{(1+a^3)(1+b^3)}}=\sum\frac{a^2}{\sqrt{(1+a)(a^2-a+1)}.\sqrt{(1+b)(b^2-b+1)}}\ge \sum\frac{4a^2}{(b^2+2)(c^2+2)}[/TEX]
cần c/m: [TEX]\sum \frac{a^2}{(a^2+2)(b^2+2)}\ge \frac{1}{3}[/TEX]
\Leftrightarrow[TEX] 2 \sum\ a^2 +\sum \ a^2b^2\ge 72[/TEX] (AM-GM)
Cho các số dương [TEX]a,b,c[/TEX] chứng minh rằng
[TEX]\sum_{cyclic}\frac{a^2}{2a^2+bc}\le 1[/TEX]
đã lâu lắm rồi mình ko làm bdt[TEX]ab+bc+ac=1.a,b,c>0[/TEX]
CM :
[TEX]\prod_{cyclic}(a^2+2b^2+3) \ge 64[/TEX]

