B
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
- Status
- Không mở trả lời sau này.
B
bboy114crew
P
phantom_lady.vs.kaito_kid
Cho a,b,c là các số thực dương t/m [TEX]\frac{a}{b}+\frac{b}{c}+\frac{c}{a}=5[/TEX]
Cmr [TEX]\frac{17}{4} \leq \frac{b}{a}+\frac{c}{b}+\frac{a}{c} \leq 1+4\sqrt{2}[/TEX]
Chú ý latex
http://diendan.hocmai.vn/showthread.php?p=1489643#post1489643
P
phantom_lady.vs.kaito_kid
Cho a,b,c là các số thực dương t/m [TEX]\frac{a}{b}+\frac{b}{c}+\frac{c}{a}=5[/TEX]
Cmr [TEX]\frac{17}{4} \leq \frac{b}{a}+\frac{c}{b}+\frac{a}{c} \leq 1+4\sqrt{2}[/TEX]
Chú ý latex
http://diendan.hocmai.vn/showthread.php?p=1489643#post1489643
A
azuredragonzx
A
azuredragonzx
H
huu_thuong
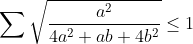
Nếu bài này là \geq 1 thì dùng CBS và schur là ra!
Nhưng mà học bắt chứng minh nhỏ hơn hoặc bằng 1 mà bạn /
Nếu mà lớn hơn hoặc bằng 1 thì làm gì có giá trị của x, y, z ?
H
huu_thuong
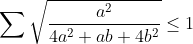
Nếu bài này là \geq 1 thì dùng CBS và schur là ra!
Nhưng mà học bắt chứng minh nhỏ hơn hoặc bằng 1 mà bạn /
Nếu mà lớn hơn hoặc bằng 1 thì làm gì có giá trị của x, y, z ?
0
01263812493
[TEX]\blue x,y,z \in [1;4]; \ x \geq y, \ x \geq z. \ Min:[/TEX]
[TEX]\blue P=\frac{x}{2x+3y}+ \frac{y}{y+z}+ \frac{z}{z+x}[/TEX]
[TEX]\blue P=\frac{x}{2x+3y}+ \frac{y}{y+z}+ \frac{z}{z+x}[/TEX]
0
01263812493
[TEX]\blue x,y,z \in [1;4]; \ x \geq y, \ x \geq z. \ Min:[/TEX]
[TEX]\blue P=\frac{x}{2x+3y}+ \frac{y}{y+z}+ \frac{z}{z+x}[/TEX]
[TEX]\blue P=\frac{x}{2x+3y}+ \frac{y}{y+z}+ \frac{z}{z+x}[/TEX]
M
miko_tinhnghich_dangyeu
[TEX]\blue x,y,z \in [1;4]; \ x \geq y, \ x \geq z. \ Min:[/TEX]
[TEX]\blue P=\frac{x}{2x+3y}+ \frac{y}{y+z}+ \frac{z}{z+x}[/TEX]
chủ yếu các đáp án bài này thường dùng đạo hàm , nhưng lớp 9 chưa học đến , nên mình có cách này :trong đề ĐH khối A năm nay
Đặt [TEX]x=4a, y=b, z=2c (a,b,c>0)[/TEX]. Đưa BDT đã cho về [TEX]\frac{4a}{8a+3b}+\frac{b}{b+2c}+\frac{c}{c+2a}[/TEX]
Đầu tiên xét BDT phụ [TEX]\frac{4a}{8a+3b} \geq \frac{a}{a+2b}+\frac1{33} \leftrightarrow \frac4{8+3\frac{b}{a}} \geq \frac1{1+2\frac{b}{a}}+\frac1{33}[/TEX]. Đặt [TEX]\frac{b}{a}=t[/TEX] với [TEX]1 \leq t \leq 16[/TEX] (do đề bài), rút gọn lại về [TEX]3t^2-73t+70 \leq 0 \Leftrightarrow (t-1)(3t-70) \leq 0[/TEX] đúng.
Đến đây chỉ còn lại tìm min của [TEX]\frac{a}{a+2b}+\frac{b}{b+2c}+\frac{c}{c+2a} [/TEX]
[TEX]=\frac{a^2}{a^2+2ab}+\frac{b^2}{b^2+2bc}+\frac{c^2}{c^2+2ca} \geq \frac{(a+b+c)^2}{a^2+2ab+b^2+2bc+c^2+2ca} =1.[/TEX]
Min của biểu thức bằng 34/33 đạt được khi x=4, y=1, z=2.
M
miko_tinhnghich_dangyeu
[TEX]\blue x,y,z \in [1;4]; \ x \geq y, \ x \geq z. \ Min:[/TEX]
[TEX]\blue P=\frac{x}{2x+3y}+ \frac{y}{y+z}+ \frac{z}{z+x}[/TEX]
chủ yếu các đáp án bài này thường dùng đạo hàm , nhưng lớp 9 chưa học đến , nên mình có cách này :trong đề ĐH khối A năm nay
Đặt [TEX]x=4a, y=b, z=2c (a,b,c>0)[/TEX]. Đưa BDT đã cho về [TEX]\frac{4a}{8a+3b}+\frac{b}{b+2c}+\frac{c}{c+2a}[/TEX]
Đầu tiên xét BDT phụ [TEX]\frac{4a}{8a+3b} \geq \frac{a}{a+2b}+\frac1{33} \leftrightarrow \frac4{8+3\frac{b}{a}} \geq \frac1{1+2\frac{b}{a}}+\frac1{33}[/TEX]. Đặt [TEX]\frac{b}{a}=t[/TEX] với [TEX]1 \leq t \leq 16[/TEX] (do đề bài), rút gọn lại về [TEX]3t^2-73t+70 \leq 0 \Leftrightarrow (t-1)(3t-70) \leq 0[/TEX] đúng.
Đến đây chỉ còn lại tìm min của [TEX]\frac{a}{a+2b}+\frac{b}{b+2c}+\frac{c}{c+2a} [/TEX]
[TEX]=\frac{a^2}{a^2+2ab}+\frac{b^2}{b^2+2bc}+\frac{c^2}{c^2+2ca} \geq \frac{(a+b+c)^2}{a^2+2ab+b^2+2bc+c^2+2ca} =1.[/TEX]
Min của biểu thức bằng 34/33 đạt được khi x=4, y=1, z=2.
P
pipi2
ơ đây là đề đại học khối A vừa mới thi mà ,[TEX]\blue x,y,z \in [1;4]; \ x \geq y, \ x \geq z. \ Min:[/TEX]
[TEX]\blue P=\frac{x}{2x+3y}+ \frac{y}{y+z}+ \frac{z}{z+x}[/TEX]
t chỉ biết bài này dùng dồn biến biểu thức chứ chưa làm bao h
không thì lên mạng tìm đáp án của Bộ GD cũng ok
P
pipi2
ơ đây là đề đại học khối A vừa mới thi mà ,[TEX]\blue x,y,z \in [1;4]; \ x \geq y, \ x \geq z. \ Min:[/TEX]
[TEX]\blue P=\frac{x}{2x+3y}+ \frac{y}{y+z}+ \frac{z}{z+x}[/TEX]
t chỉ biết bài này dùng dồn biến biểu thức chứ chưa làm bao h
không thì lên mạng tìm đáp án của Bộ GD cũng ok
K
khanh_ndd
Đặt [TEX]x=\frac{b}{a},....[/TEX]cho a,b,c>0 . chứng minh:
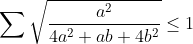
BĐT trở thành [TEX]\sum \frac{1}{\sqrt{4x^2+x+4}}\le 1[/TEX] với [TEX]xyz=1[/TEX]
Chú ý [TEX]\frac{1}{\sqrt{4x^2+x+4}}\le \frac{x+1}{2(x^2+x+1)}=\frac{1}{2}-\frac{1}{2(\frac{1}{x^2}+\frac{1}{x}+1)}[/TEX]
nên ta cần chứng minh: [TEX]\frac{3}{2}-\frac{1}{2}.\sum \frac{1}{\frac{1}{x^2}+\frac{1}{x}+1}\le 1[/TEX]
hay [TEX]\sum \frac{1}{\frac{1}{x^2}+\frac{1}{x}+1}\ge 1[/TEX]
nhưng đây là 1 BĐT quen thuộc và có nhiều ứng dụng.
Last edited by a moderator:
K
khanh_ndd
Đặt [TEX]x=\frac{b}{a},....[/TEX]cho a,b,c>0 . chứng minh:
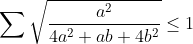
BĐT trở thành [TEX]\sum \frac{1}{\sqrt{4x^2+x+4}}\le 1[/TEX] với [TEX]xyz=1[/TEX]
Chú ý [TEX]\frac{1}{\sqrt{4x^2+x+4}}\le \frac{x+1}{2(x^2+x+1)}=\frac{1}{2}-\frac{1}{2(\frac{1}{x^2}+\frac{1}{x}+1)}[/TEX]
nên ta cần chứng minh: [TEX]\frac{3}{2}-\frac{1}{2}.\sum \frac{1}{\frac{1}{x^2}+\frac{1}{x}+1}\le 1[/TEX]
hay [TEX]\sum \frac{1}{\frac{1}{x^2}+\frac{1}{x}+1}\ge 1[/TEX]
nhưng đây là 1 BĐT quen thuộc và có nhiều ứng dụng.
K
khanh_ndd
Mấy bài giải trí
1. Cho [TEX]a,b,c>0, a+b+c=1[/TEX]. Tìm max của biểu thức:
[TEX]A=\sqrt{a^2+abc}+\sqrt{b^2+abc}+\sqrt{c^2+abc}+ \sqrt{9abc}[/TEX]
2. Cho [TEX]a,b,c,d[/TEX] là các số thực dương thỏa mãn [TEX]a+b+c+d=a^2+b^2+c^2+d^2[/TEX]
Chứng minh: [TEX]2(a^3+b^3+c^3+d^3)+a+b+c+d\le 12[/TEX]
bài thứ 2 đơn giản hơn nhiều so với bài này
1. Cho [TEX]a,b,c>0, a+b+c=1[/TEX]. Tìm max của biểu thức:
[TEX]A=\sqrt{a^2+abc}+\sqrt{b^2+abc}+\sqrt{c^2+abc}+ \sqrt{9abc}[/TEX]
2. Cho [TEX]a,b,c,d[/TEX] là các số thực dương thỏa mãn [TEX]a+b+c+d=a^2+b^2+c^2+d^2[/TEX]
Chứng minh: [TEX]2(a^3+b^3+c^3+d^3)+a+b+c+d\le 12[/TEX]
bài thứ 2 đơn giản hơn nhiều so với bài này
Max nó là [TEX]2+\frac{7}{2\sqrt{3}[/TEX] @-)
Bài 1: Cho các số dương a,b,c thỏa mãn [TEX]\ DK\ a+b+c+d=a^2+b^2+c^2+d^2[/TEX]
Tìm GTLN của [TEX]: a^3+b^3+c^3+d^3[/TEX]
K
khanh_ndd
Mấy bài giải trí
1. Cho [TEX]a,b,c>0, a+b+c=1[/TEX]. Tìm max của biểu thức:
[TEX]A=\sqrt{a^2+abc}+\sqrt{b^2+abc}+\sqrt{c^2+abc}+ \sqrt{9abc}[/TEX]
2. Cho [TEX]a,b,c,d[/TEX] là các số thực dương thỏa mãn [TEX]a+b+c+d=a^2+b^2+c^2+d^2[/TEX]
Chứng minh: [TEX]2(a^3+b^3+c^3+d^3)+a+b+c+d\le 12[/TEX]
bài thứ 2 đơn giản hơn nhiều so với bài này
1. Cho [TEX]a,b,c>0, a+b+c=1[/TEX]. Tìm max của biểu thức:
[TEX]A=\sqrt{a^2+abc}+\sqrt{b^2+abc}+\sqrt{c^2+abc}+ \sqrt{9abc}[/TEX]
2. Cho [TEX]a,b,c,d[/TEX] là các số thực dương thỏa mãn [TEX]a+b+c+d=a^2+b^2+c^2+d^2[/TEX]
Chứng minh: [TEX]2(a^3+b^3+c^3+d^3)+a+b+c+d\le 12[/TEX]
bài thứ 2 đơn giản hơn nhiều so với bài này
Max nó là [TEX]2+\frac{7}{2\sqrt{3}[/TEX] @-)
Bài 1: Cho các số dương a,b,c thỏa mãn [TEX]\ DK\ a+b+c+d=a^2+b^2+c^2+d^2[/TEX]
Tìm GTLN của [TEX]: a^3+b^3+c^3+d^3[/TEX]
T
thienlong_cuong
1. Cho [TEX]a,b,c>0, a+b+c=1[/TEX]. Tìm max của biểu thức:
[TEX]A=\sqrt{a^2+abc}+\sqrt{b^2+abc}+\sqrt{c^2+abc}+ \sqrt{9abc}[/TEX]
2. Cho [TEX]a,b,c,d[/TEX] là các số thực dương thỏa mãn [TEX]a+b+c+d=a^2+b^2+c^2+d^2[/TEX]
Chứng minh: [TEX]2(a^3+b^3+c^3+d^3)+a+b+c+d\le 12[/TEX]
bài thứ 2 đơn giản hơn nhiều so với bài này
Max nó là [TEX]2+\frac{7}{2\sqrt{3}[/TEX] @-)
tia câu a mà chém 1 Thấy có ý tưởng !
[TEX]abc \leq \frac{1}{27} \Rightarrow \sqrt{\frac{4}{3}.9abc} \leq \sqrt{\frac{4}{9}} = \frac{2}{3} [/TEX]
Xét :
[TEX]\sqrt{\frac{4}{3}.(a^2 + abc)} = \sqrt{\frac{4}{3}.a(a + bc)} \leq \frac{\frac{4}{3}a + a + bc}{2} = \frac{7}{6}a + \frac{bc}{2} [/TEX]
Xây dựng tương tự \Rightarrow Ta có :
[TEX]\sqrt{\frac{4}{3}}A \leq \frac{2}{3} + \frac{7}{6}(a + b + c) + \frac{ab + bc + ac}{2} \leq \frac{2}{3} + \frac{7}{6} + \frac{1}{6} = 2[/TEX]
[TEX]\Rightarrow A \leq \sqrt{3}[/TEX]
Last edited by a moderator:
T
thienlong_cuong
1. Cho [TEX]a,b,c>0, a+b+c=1[/TEX]. Tìm max của biểu thức:
[TEX]A=\sqrt{a^2+abc}+\sqrt{b^2+abc}+\sqrt{c^2+abc}+ \sqrt{9abc}[/TEX]
2. Cho [TEX]a,b,c,d[/TEX] là các số thực dương thỏa mãn [TEX]a+b+c+d=a^2+b^2+c^2+d^2[/TEX]
Chứng minh: [TEX]2(a^3+b^3+c^3+d^3)+a+b+c+d\le 12[/TEX]
bài thứ 2 đơn giản hơn nhiều so với bài này
Max nó là [TEX]2+\frac{7}{2\sqrt{3}[/TEX] @-)
tia câu a mà chém 1 Thấy có ý tưởng !
[TEX]abc \leq \frac{1}{27} \Rightarrow \sqrt{\frac{4}{3}.9abc} \leq \sqrt{\frac{4}{9}} = \frac{2}{3} [/TEX]
Xét :
[TEX]\sqrt{\frac{4}{3}.(a^2 + abc)} = \sqrt{\frac{4}{3}.a(a + bc)} \leq \frac{\frac{4}{3}a + a + bc}{2} = \frac{7}{6}a + \frac{bc}{2} [/TEX]
Xây dựng tương tự \Rightarrow Ta có :
[TEX]\sqrt{\frac{4}{3}}A \leq \frac{2}{3} + \frac{7}{6}(a + b + c) + \frac{ab + bc + ac}{2} \leq \frac{2}{3} + \frac{7}{6} + \frac{1}{6} = 2[/TEX]
[TEX]\Rightarrow A \leq \sqrt{3}[/TEX]
- Status
- Không mở trả lời sau này.

