[Toán 8] Chuyên Đề Bất Đẳng Thức

T

trangkhanhkhoi

trydan said:
Cho a, b, c > 0 và
gif.latex
. Chứng minh rằng: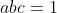
gif.latex

@anh bigbang195 không làm nha :( ;;)
Bấm để xem đầy đủ nội dung ...
Tớ làm thử nha
Ta có : [tex]a,b,c>0[/tex]
[tex]\Rightarrow ab+bc+ac>0[/tex]
Ta có :
[tex]\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{6}{a+b+c}[/tex]
[tex]\Leftrightarrow\frac{bc(a+b+c)+ac(a+b+c)+bc(a+b+c)+6}{a+b+c}[/tex]
[tex]\Leftrightarrow\frac{(a+b+c)(ab+bc+ac)+6}{a+b+c}[/tex]
[tex]\Leftrightarrow(ab+bc+ac)+6[/tex]
Mà [tex](ab+bc+ac)>0[/tex] (CMT)
[tex]\Rightarrow(ab+bc+ac)+6>6[/tex]
[tex]\Leftrightarrow(ab+bc+ac)+6\geq 5[/tex]
Vậy [tex]\Rightarrow \frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{6}{a+b+c} \geq 5[/tex] (đpcm)
 
Last edited by a moderator:
0

01263812493

trangkhanhkhoi said:
Tớ làm thử nha

[tex]\Rightarrow(ab+bc+ac)+6>6[/tex]
[tex]\Leftrightarrow(ab+bc+ac)+6\geq 5[/tex]
Bấm để xem đầy đủ nội dung ...

ủa sao ngộ thế nếu [TEX](ab+bc+ac)+6>6 [/TEX] thì [TEX](ab+bc+ac)+6\geq 7[/TEX] chứ sao lớn hơn hoặc bằng 5 với lại mình nghĩ [TEX](ab+bc+ac)+6 \geq 3\sqrt[3]{a^2b^2c^2}+6 =9 [/tex] ----> vậy hổng lẻ đề sai ---- > mà mình mong các bạn giải BDT bằng kiến thức lớp 8 --- chứ như bạn Bigbang95 thì mình chả hiểu - sr tại mình kém :D
__________________________________:D
 
Last edited by a moderator:
T

trydan

Theo yêu cầu của 0915549009 :D
Cho a, b, c > 0. Chứng minh rằng :
gif.latex


______________________________________________________________
Đừng háo thắng mà không đi xa được , việc học cũng giống như chạy marathon 42 km, phải biết giữ sức, những cây số đầu không mấy quan trọng, không học nhồi học nhét, không ham ánh hào quang hão huyền, làm sao để càng về sau càng khổng lồ, đó mới là kết quả thật sự.

 
Last edited by a moderator:
Q

quan8d

trydan said:
Theo yêu cầu của 0915549009 :D
Cho a, b, c > 0. Chứng minh rằng :
gif.latex
Bấm để xem đầy đủ nội dung ...
đây là cách đơn giản phù hợp với trình độ bình thường, tham khảo nha
\Leftrightarrow [tex]a^8+b^8+c^8 \geq a^2b^3c^3+a^3b^2c^3+a^3b^3c^2 = a^2b^2c^2(ab+bc+ca)[/tex]
Cô si : [tex]a^8+b^8 \geq 2a^4b^4[/tex]
[tex]b^8+c^8 \geq 2b^4c^4[/tex]
[tex]c^8+a^8 \geq 2c^4a^4[/tex]
\Rightarrow [tex]a^8+b^8+c^8 \geq a^4b^4+b^4c^4+c^4a^4[/tex]
Tương tự cách trên: [tex]a^4b^4+b^4c^4+c^4a^4 \geq a^2b^2c^2(a^2+b^2+c^2)[/tex]
mà [tex]a^2+b^2+c^2 \geq ab+bc+ca[/tex]
từ đó có đpcm
 
K

khoan1199

jhj

Mình làm thử nhé
vì x,y,z>0 nên chia xyz xuống suy ra 1\(yz)+1\(xz) >= 16
1\(yz)+1\(xz)>=4\z(x+y)
vì x+y+z=1 =>x+y=1-z
dễ dành chứng minh 4\(z-z^2)>=16
 
I

ilovetoan

trydan said:
Cho a, b, c > 0 và
gif.latex
. Chứng minh rằng:
gif.latex

@anh bigbang195 không làm nha :( ;;)


______________________________________________________________
Đừng háo thắng mà không đi xa được , việc học cũng giống như chạy marathon 42 km, phải biết giữ sức, những cây số đầu không mấy quan trọng, không học nhồi học nhét, không ham ánh hào quang hão huyền, làm sao để càng về sau càng khổng lồ, đó mới là kết quả thật sự.
Bấm để xem đầy đủ nội dung ...
vì a,b,c có vai trò như nhau nên giả sử a\geqb\geqc \Rightarrowc\leq1 (vì abc =1)
\Rightarrowdpcm
 
J

jenie_k19

trydan said:
Mình có 2 bất đẳng thức sau, mọi người giải giúp nhé:
1) Cho [TEX]a, b, c>0[/TEX]. Chứng minh rằng: [TEX]\frac{a}{b+c}+\frac{b}{c+d}+\frac{c}{d+a}+\frac{d}{a+b}\geq2[/TEX]
2) Cho [TEX]a+b+c=4 [/TEX] và [TEX] a, b, c>0[/TEX]. Chứng minh rằng:[TEX] (a+b)(b+c)(c+a)\geq a^3b^3c^3[/TEX]
Bấm để xem đầy đủ nội dung ...

rua_it said:
[tex]LHS:=\frac{a}{b+c}+\frac{b}{c+d}+\frac{c}{d+a}+ \frac{d}{a+b}[/tex]

[tex]=\frac{a^2}{ab+ac}+\frac{b^2}{bc+bd}+\frac{c^2}{cd+ca}+\frac{d^2}{da+db}[/tex]

[tex] \geq \frac{(a+b+c+d)^2}{ab+ac+bc+bd+cd+ca+da+db}[/tex]

Cần chứng minh [tex]2.(\sum_{sym} ab+ac+bd) \leq (a+b+c+d)^2[/tex]

[tex]\Leftrightarrow a^2+b^2+c^2+d^2+2.(ab+bc+cd+ac+bd) \geq 2.(\sum_{sym} ab+ac+bd)[/tex]

[tex]\Leftrightarrow (a-c)^2+(b-d)^2 \geq 0[/tex]

Bất đẳng thức cuối luôn đúng.
Bấm để xem đầy đủ nội dung ...

Bài 1 thì theo mình giải cách này hay hơn:
[TEX]VT+2=\frac{a+b}{b+c}+\frac{b+c}{c+d}+\frac{c+d}{d+a}+\frac{d+a}{a+b}\geq 4[/TEX] (BĐT AM - GM)
\Rightarrow VT \geq 2
 
Last edited by a moderator:
0

0915549009

Tương tự cách trên: [tex]a^4b^4+b^4c^4+c^4a^4 \geq a^2b^2c^2(a^2+b^2+c^2)[/tex]
Các bạn có thể nói rõ đoạn này hơn đc hok?
 
R

rooney_cool

Lớp 8

Cho [TEX]x,y > 0[/TEX] và [TEX]x + y \geq 6[/TEX]. Tìm [TEX]Min[/TEX]

[TEX]A= 3x + 2y + \frac{6}{x}+\frac{8}{y}[/TEX]​
 
Last edited by a moderator:
H

helmay

đề bài này:
cho tam giác ABC. lấy điểm M ở miền trong tam giác, các đường thẳng AM, BM,CM cắt các cạnh của tam giác lần lượt tại các điểm A1, B1, C1 . chứng minh:
gif.latex

gợi ý : có sử dụng bất đẳng thức phụ
gif.latex

chú ý latex
 
Last edited by a moderator:
Q

quan8d

helmay said:
đề bài này:
cho tam giác ABC. lấy điểm M ở miền trong tam giác, các đường thẳng AM, BM,CM cắt các cạnh của tam giác lần lượt tại các điểm A1, B1, C1 . chứng minh:
AM/A1M + BM / B1M + CM / C1M >= 6
gợi ý : có sử dụng bất đẳng thức phụ x + 1/x >= 2 ( x>0)
Bấm để xem đầy đủ nội dung ...
Gọi [tex]{S}_{AMB} , {S}_{AMC} , {S}_{MBC}[/tex] lần lượt là [tex]S_1 , S_2 , S_3[/tex]
Ta có : [tex]\frac{AM}{A_1M} = \frac{S_1}{{S}_{A_1BM}} = \frac{S_2}{{S}_{A_1CM}} = \frac{S_1+S_2}{S_3}[/tex]
Tương tự : [tex]\frac{BM}{B_1M} = \frac{S_1+S_3}{S_2} [/tex]
[tex]\frac{CM}{C_1M} = \frac{S_2+S_3}{S_1}[/tex]
[tex]\Rightarrow \frac{AM}{A_1M}+\frac{BM}{B_1M}+\frac{CM}{C_1M} = \frac{S_1+S_2}{S_3}+\frac{S_1+S_3}{S_2}+\frac{S_2+S_3}{S_1} \geq 6 [/tex](đpcm)
 
Last edited by a moderator:
You must log in or register to reply here.
Top Bottom