[LTDH] Phương pháp tọa độ trong mặt phẳng

[teoke1234]

share mình đề dự bị khối B với bạn ơi
.............................................

Trích đề dự bị khối B năm 2010

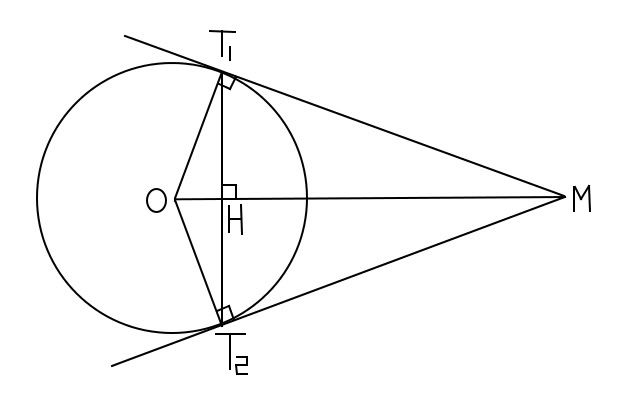
Trong mât phẳng tọa độ Oxy, cho đường tròn (C):

, tâm i và điểm A(1+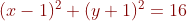

,1). Chứng minh mọi đường thẳng đi qua A đều cắt (C) tại 2 điểm phân biệt. Viết phương trình đường thẳng d đi qua A và cắt (C) tại 2 điểm B,C sao cho tam giác IBC không có góc tù và có diện tích bằng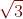

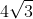
cm dt qua A cắt ở 2 điểm thì chỉ cần cm A nằm trong đường tròn
IA = [TEX]\sqrt{7}<R[/TEX]
[TEX]SIBC=4\sqrt{3}=0.5 . BC .IH [/TEX]
mà BC = [TEX]2\sqrt{R^2 -IH^2}[/TEX]
thế vào pt trên giải ra 2 IH=2 hoặc IH=[TEX]2\sqrt{3}[/TEX]
với IH =2 suy ra BC =[TEX]4\sqrt{3}[/TEX] theo định lý hàm số cos suy ra góc BIC =120 độ nên trường hợp này loại
trường hơp IH=[TEX]2\sqrt{3}[/TEX] suy ra BC = 4 nên tam giác IBC đều nên thoả mãn
từ đây lập pt BC qua A([TEX]\sqrt{3}+1,1[/TEX]) và khoảng cách từ I đến BC = [TEX]\2sqrt{3}[/TEX]
đến đây không hiểu sao mình lập BC k thê lập được toàn ra vô nghiệm thôi :|

 

[ryelax]

share mình đề dự bị khối B với bạn ơi
.............................................

Đề dự bị khối B 2010

http://www.mediafire.com/?iaet17g3ibbcko9

....................................................

 

[tan75]

bà con cô bác giúp con bài này
cho hình thang ABCD vuông tại A VÀ D có BC=2AB trung điễm BC là M(1;0) đường thẳng AD là x-y=0 tìm tọa dộ A

 

[ryelax]

thêm câu tọa độ mặt phẳng trong đề 2010 dự bị nữa nè:

Cho (C) :

và điểm K(3;4). Viết phương trình đường tròn tâm K, cắt (C) tại A và B sao cho AB là một cạnh hình vuông có 4 đỉnh thuộc (C)

 

[ngomaithuy93]

Cho (C) :

và điểm K(3;4). Viết phương trình đường tròn tâm K, cắt (C) tại A và B sao cho AB là một cạnh hình vuông có 4 đỉnh thuộc (C)

(C) có tâm I(3;-1), bán kính R=4
Giả sử AB là 2 cạnh của hvg ABCD \Rightarrow BD=2R=8 \Rightarrow AB=2.
Gọi M là giao điểm của IK và AB.
Ta có:
IA=R=4
MA=MB=1
IK=5
[TEX]\Rightarrow IM=\sqrt{15} \Rightarrow MK=5-\sqrt{15}[/TEX]
[TEX]\Rightarrow KA=KB=\sqrt{KM^2+MA^2}=\sqrt{41-10\sqrt{15}}=R'[/TEX]
\Rightarrow pt đường tròn...

Cả nhà đi thi cả rồi sao? (

 

[ngomaithuy93]

cho hình thang ABCD vuông tại A VÀ D có BC=2AB trung điễm BC là M(1;0) đường thẳng AD là x-y=0 tìm tọa dộ A

Gọi I là hình chiếu vg góc của M trên AD [TEX]\Rightarrow I(\frac{1}{2};\frac{1}{2})[/TEX]
[TEX]MI=\frac{1}{\sqrt{2}}[/TEX]
A(a;a)
[TEX]IA^2+MI^2=MA^2 \Leftrightarrow 2(a-\frac{1}{2})^2+\frac{1}{2}=(a-1)^2+a^2 \Leftrightarrow a=... \Rightarrow A[/TEX]

Đợi t với (

 

[ryelax]

Ngủ nghỉ chuẩn bị đi thi thôi nào các bạn hiền!!! mình chúc các bạn đạt kết quả tốt, chuẩn bị khăn gói lên đường lên kinh ứng thí thôi ,chúc mod Thúy thi đỗ nhé !!!

 

[tan75]

ủa bài của mình bị xóa vậy bài của ngôimaithuy93 dúng rồi à có ai giải thích dùm mình ko sao dữ kiện bạn ấy chưa sài hết ,mà phương trình cuối giải ko ra a

Dữ kiện đã xài hết !!
Bài toán có nhiều đáp số

 

[tan75]

trong mặt phẳng tọa độ cho đường tròn C (x-1)^2 + (y+3)^2=81 Nviết phương trình dt d biết d đi qua M(1;3) VÀ cắt C tạo thành dây cung có độ dài nhỏ nhất

 

[duynhan1]

trong mặt phẳng tọa độ cho đường tròn C (x-1)^2 + (y+3)^2=81 Nviết phương trình dt d biết d đi qua M(1;3) VÀ cắt C tạo thành dây cung có độ dài nhỏ nhất

1. M nằm trong đường tròn
2. Dây cung nhỏ nhất thì khoảng cách từ tâm I đến d là lớn nhất
   
3. [TEX]d_{max} = IM [/TEX]

 

[tan75]

còn BC=2AB mà anh nhân bài này là câu dự bi 2010 mà em nghĩ đề thi đại học ít khi có vô số dáp án

 

[duynhan1]

còn BC=2AB mà anh nhân bài này là câu dự bi 2010 mà em nghĩ đề thi đại học ít khi có vô số dáp án

BC = 2AB <--> AB = BM

bà con cô bác giúp con bài này
cho hình thang ABCD vuông tại A VÀ D có BC=2AB trung điễm BC là M(1;0) đường thẳng AD là x-y=0 tìm tọa dộ A

Bài này anh lập luận thế này!
BM = khoảng cách từ B đến đường thẳng AD, nên B thuộc parbol có tiêu điểm là M và đường chuẩn delta.

Như vậy ứng với 1 điểm B nằm trên parabol hạ BA vuông góc với đường thẳng AD thì ta có BA=BM. Lấy điểm C đối xứng với điểm B qua điểm M thì khi đó 2AB = BC. Hạ C vuông góc với AD thì ta có được 1 hình thang ABCD thỏa mãn yêu cầu bài toán.

 

[destinyx4]

Mình xin giải theo cách khác

Nhỡ đặt tâm là O rồi, dùng O vậy. Toạ độ là O(1; 2).

Dễ thấy [tex]T_1T_2 \perp OM[/tex] nên [tex]\vec{OM} = (4;1)[/tex] là vecto pháp tuyến của [tex]T_1T_2.[/tex]

[tex]\Delta T_1HM \sim \Delta OT_1M \Rightarrow \fr{T_1M}{HM} = \fr{OM}{T_1M} \Rightarrow T_1M^2 = OM.HM = OM^2 - OT_1^2 \Rightarrow HM = \fr{OM^2-R^2}{OM} = \fr{13}{\sqr{17}}[/tex]

Ta có [tex]\vec{HM} = (5-x;3-y) \Rightarrow HM^2 = (5-x)^2+(3-y)^2 = \fr{169}{17}[/tex]

Một vecto chỉ phương của [tex]T_1T_2[/tex] là [tex]\vec{u} = (1;-4)[/tex]

[tex]\vec{HM} \perp \vec{u} \Rightarrow (5-x)=4(3-y) \Rightarrow 17(3-y)^2 = \fr{169}{17} \Rightarrow (3- y)^2 = \fr{169}{289} \Rightarrow \left\[y = \fr{38}{17}\\y = \fr{64}{17}[/tex]

[tex]\Rightarrow \left\[\vec{HM}=(\fr{33}{17};\tex{ }\fr{13}{17})\\\vec{HM}=(\fr{137}{17};\tex{ }-\fr{13}{17})[/tex]

Vecto đầu tiên nhận vì cùng hướng với [tex]\vec{OM} \Rightarrow T_1T_2:\tex{ }4x+y-10=0[/tex]

Sao ra khác nhóc Ngố nhỷ

Bài này đang còn một cách nữa:
Gọi T(xo;yo) và T thuộc đường tròn.Do T là tiếp điểm của tiếp tuyến kẻ đến đưởng tròn nên ta có:
véctơ MT vuông góc với vectơ IT =>(xo-5)(xo-1)+(yo-3)(yo-2)=0
<=> xo^2+yo^2-6xo-5yo+11=0 (1)
Lại có T thuộc đường tròn nên (xo-1)^2+(yo-2)^2=4
<=>xo^2-2xo+yo^2-4yo+1=0 (2)
Lấy (1)-(2)=>-4xo-yo+10=0
=>Vậy toạ độ của tất cả các tiếp điểm từ M kẻ đến đường tròn đều thuộc biểu thức trên <do ta đã gọi T(x0;y0) là tiếp điểm của các tiếp điểm từ M đến đường tròn>
Vậy pt cần tìm là -4x-y+10=0

 

[chiro006]

Trong mf Oxy cho A(1;1) ; B(3;2) ; C(7;10) . Viết pt đt d qua A sao cho tổng khoảng cách từ B, C đến d lớn nhất

 

[duynhan1]

Gọi d là tổng khoảng cách từ B và C đến (d).
[tex] d: ax+by - a - b= 0 \ (a^2+b^2 \not= 0 ) \\ d(B;d) = \frac{|2a+b|}{\sqrt{a^2+b^2}} \\ d(C;d) = \frac{|6a+9b|}{\sqrt{a^2+b^2}} [/tex]
[TEX]d= d(B;d)+ d(C;d) = \frac{|2a+b| + 3|2a+3b|}{\sqrt{a^2+b^2}} \le \frac{8|a| + 10|b| }{\sqrt{a^2+b^2}} \le \frac{\sqrt{8^2+10^2} \sqrt{a^2+b^2} }{\sqrt{a^2+b^2}} = 2 \sqrt{41}[/TEX]
Dấu "=" xảy ra khi và chỉ khi :
[TEX]\left{ ab \ge 0 \\ \frac{|a|}{8} = \frac{|b|}{10} \right. \\ \Leftrightarrow a= \frac45 b [/TEX]
Chọn [TEX]a= 4 \Rightarrow b=5[/TEX], và khi đó [TEX]d:\ 4x + 5y - 9 = 0[/TEX]
Vậy [TEX]d:\ 4x + 5y - 9 =0 [/TEX] thì tổng khoảng cách từ B và C đến d là lớn nhất

 

[myhien_1710]

Trong mặt phẳng Oxy ,cho các đường thẳng d1 : 2x-3y-3=0 và d2: 5x+2y-17=0 .Viết phương trình đường thẳng d đi qua giao điểm của d1 và d2 cắt các tia Ox ,Oy lần lượt tại các điểm A và B sao cho [TEX] \frac{AB^2}{(dt\large\Delta OAB)^2[/TEX] nhỏ nhất

 

[hocmai.toanhoc]

Trong mặt phẳng Oxy ,cho các đường thẳng d1 : 2x-3y-3=0 và d2: 5x+2y-17=0 .Viết phương trình đường thẳng d đi qua giao điểm của d1 và d2 cắt các tia Ox ,Oy lần lượt tại các điểm A và B sao cho [TEX] \frac{AB^2}{(dt\large\Delta OAB)^2[/TEX] nhỏ nhất

Chào em!
Hocmai.toanhoc gợi ý em làm bài này nhé!
- B1: Tọa độ giao điểm của d1 và d2 là M(3;1)
-B2: Gọi d: đi qua M có hệ số góc k, d có phương trình là: y = k(x-3)+1.
- B3: Tìm tọa độ giao điểm giữa d là trục Ox, Oy ta có tọa độ A, B.
- B4: Thay vào biểu thức tìm điều kiện của k để biểu thức min.
S tam giác vuông =[TEX]=\frac{1}{2}OA.OB[/TEX]

 

[giaosu_fanting_thientai]

Trong mặt phẳng Oxy cho đường thẳng d : [TEX](1-m^2)x+2my+m^2-4m+1=0[/TEX]
Viết phương trình đường tròn luôn tiếp xúc (d)

 

[duynhan1]

Trong mặt phẳng Oxy cho đường thẳng d : [TEX](1-m^2)x+2my+m^2-4m+1=0[/TEX]
Viết phương trình đường tròn luôn tiếp xúc (d)

Điều kiện cần:
Giả sử tồn tại đường tròn (C) mà d luôn tiếp xúc (C).
Gọi [TEX]M(x_o;y_o)[/TEX] là điểm mà d không bao giờ đi qua, ta có:
[TEX](1-m^2) x_o + 2m_o y +m^2 -4m + 1 \not= 0 \forall m \\ \Leftrightarrow (1-x_o)m^2 + 2(y_o-2) m + x_o + 1 = 0 \\ \Leftrightarrow \left[ \left{ 1-x_o=0 \\ y_o-2 = 0 \\ x_o+1 \not= 0 \right. \\ \left{ 1-x_o \not = 0 \\ (y_o-2)^2 - (x_o+1)(1-x_o) <0 \right. \right. \\ \Leftrightarrow \left[ \left{ x_o = 1 \\ y_o= 2 \right. \\ x_o^2 + (y_o-2)^2 < 1 \right. [/TEX]
Vậy tập hợp những điểm mà d không đi qua là những điểm N(1;2) và những điểm nằm trong đường tròn [TEX](C) : x^2 + (y-2)^2 = 1[/TEX]
Do đó ta có d luôn tiếp xúc [TEX](C) : x^2 + (y-2)^2 = 1[/TEX] ( do [TEX]N(1;2) \in (C)[/TEX])
Điều kiện đủ:
Dễ chứng minh [tex] d(I;d)= R =1 [/tex] ( với I(0;2))

 

[kiburkid]

Chỉ nà d không đi qua những điểm nằm trong đường tròn đâu có nghĩa nó phải tiếp xúc với đường tròn chứ...