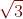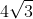S
somebody1
6) [TEX]ABCD[/TEX] là hình bình hành, [TEX]S=6 , A(1;-2); B(2;-3); I=\bigcap_{AC}^{BD} \epsilon Ox; x_I > 0[/TEX]. TÌm C,D
S
somebody1
C thuộc phân giác CD nên gọi [TEX]C(t;1-t)[/TEX]
M trung điểm của AC nên [TEX]M(\frac{t+1}{2}; \frac{3-t}{2})[/TEX]
Mặt khác M lại thuộc phân giác [TEX]BM: 2x+y+1=0[/TEX] nên thế tọa độ điểm M vào ta dc[TEX] M(2:0) \Rightarrow C(3;-2)[/TEX]
Gọi A' là điểm đôi xứng của A qua phân giác BM, và I nằm trên phân giác CD và là trung điểm của AA'.
Gọi [TEX]A'(x;y)[/TEX] => [TEX]AA'(x-1;y-2) [/TEX]// với vecto pháp tuyến của CD n(1;1)
[TEX]\Rightarrow \frac{x-1}{1}=\frac{y-2}{1} \Rightarrow d_1: x-y-3=0 (1)[/TEX]
Mặt khác I là trung điểm AA' nên [TEX]I(\frac{x+1}{2};\frac{y+2}{2})[/TEX] thuộc d: x+y-1=0 ==> [TEX]pt: x+y+1=0 (2)[/TEX]
Từ (1) và (2) ==> x=1;y=-2
[TEX]=> A'(1;-2)[/TEX]
lập pt CA' ...có dc pt CA' kết hợp với pt BM suy ra được điểm B...có B viết pt BC...ok
Last edited by a moderator:
N
ngomaithuy93
Trong mp Oxy cho A(0;1), B(2;-1) và các đ/t d1: (m-1)x+(m-2)y+2-m=0 và d2: (2-m)x+(m-1)y+3m-5=0.
CMR: d1 luôn cắt d2 với mọi giá trị m.
Gọi P là giao điểm của d1 và d2. Tìm m sao cho PA+PB lớn nhất.
CMR: d1 luôn cắt d2 với mọi giá trị m.
Gọi P là giao điểm của d1 và d2. Tìm m sao cho PA+PB lớn nhất.
N
ngomaithuy93
I(m;0) (m>0)
[TEX]\vec{AB}=(1;-1) \Rightarrow AB=\sqrt{2}[/TEX]
Dựng[TEX] AH \perp CD \Rightarrow AH=3\sqrt{2}[/TEX]
pt AB: x+y+1=0
[TEX]d_{(I,AB)}=\frac{|m+1|}{\sqrt{2}}=\frac{3}{\sqrt{2}} \Rightarrow I(2;0)[/TEX]
\Rightarrow C(3;2), D(2;3)
T
thanhduc20100
Trong mặt phẳng với hệ tọa độ Oxy, hãy xác định tọa độ đỉnh C của tam giác ABC biết rằng hình chiếu vuông góc của C lên đường thẳng AB là điểm H(-1;-1), đường phân giác trong của góc A có pt: x-y+2=0 và đường cao kẽ tù B có pt: 4x+3y-1=0
N
ngomaithuy93
[TEX] A(-23;-21)[/TEX]
[TEX]B(\frac{7}{37};\frac{3}{37})[/TEX]
[TEX]C(\frac{33}{37};\frac{-114}{37})[/TEX]
:|:|:|
S
somebody1
1) Trong mặt phẳng Oxy cho các đường thẳng [TEX]d_1: 3x-y-4=0; d_2: x+y-6=0; d_3: x-3=0[/TEX]. Tìm tọa độ các đỉnh của hình thoi [TEX]ABCD [/TEX] biết [TEX]\{BAD}[/TEX] =120, các đỉnh[TEX] A,C[/TEX] thuộc [TEX]d_3, B[/TEX] thuộc [TEX]d_1 [/TEX]và [TEX]D[/TEX] thuộc [TEX]d_2[/TEX]
Last edited by a moderator:
S
somebody1
bài này giải như sau:
H'(x;y) đối xứng với H qua phân giác góc A
HH'(x+1;y+1) // với n(1;-1) ( phân giác góc A)
[TEX]\Rightarrow\frac{x+1}{1}=\frac{y+1}{-1}\Rightarrow x+y-2=0 (1)[/TEX]
Trung điểm HH': [TEX]M(\frac{x-1}{2}\frac{y-1}{2}[/TEX] thuộc [TEX]d: x-y+2=0 \Rightarrow[/TEX] có pt: [TEX]x-y=-4 (2)[/TEX]
(1) và (2) [TEX]\left{{x+y=-2}\\{x-y=-4}\Rightarrow x=-3;y=1 \Rightarrow H'(-3;1)[/TEX]
Gọi A(a;a+2)=>H'A // với n(4;3)=> pt: 3a+9=4a+4 => a=5 => A(5:7)
Gọi C(x;y)... bạn dùng HC.HA=0 1 pt.......và AC //với H'A 2 pt==> giải hệ 2 pt ta dc C
N
ngomaithuy93
A(3;a), C(3;c), B(b;3b-4), D(d;6-d)
Trung điểm I của AB là [TEX]I(3;\frac{a+c}{2})[/TEX]
[TEX]\Rightarrow D(6-b;a+c-3b+4) \Rightarrow \left{{6-b=d}\\{6-d=a+c-3b+4}[/TEX]
[TEX]AC \perp BD \Rightarrow d+3b=10[/TEX]
\Rightarrow d=4, b=2 \Rightarrow D(4;2), B(2;2)
\Rightarrow a+c=4
AD=AB \Rightarrow a, c \Rightarrow A, C
L
luyenlishpy
2) Trong hệ Oxy chi hình bình hành [TEX]ABCD [/TEX]có [TEX]B(1,5)[/TEX], đường cao [TEX](AH): x+2y-2=0[/TEX], phân giác góc ACB là: [TEX]x-y-1=0.[/TEX] Tìm tọa độ [TEX]A,C,D[/TEX]
N
ngomaithuy93
[TEX]A(2-2a;a) \Rightarrow \vec{AB}=(2a-1;5-a)[/TEX]
[TEX]AH \perp AB \Rightarrow a=\frac{7}{5} \Rightarrow A(\frac{-4}{5};\frac{7}{5})[/TEX]
B' là điểm đối xứng với B qua đg pg trg góc ACB \Rightarrow B'(6;0)
Đt AB' chính là đt AC \Rightarrow pt đt AC: 7x+34y-42=0
[TEX]\Rightarrow C(\frac{76}{41};\frac{35}{41}) \Rightarrow D[/TEX]
L
luyenlishpy
bạn giải sai rồi cái chỗ kia AH sao vuông dc với AB....
mà đáp án nó chẵn lắm bạn AH là đg cao nên vg góc với AB mà c
c tính toán lại giúp t nhé, t hay tính toán sai lắm
L
luyenlishpy
1. Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD , có đỉnh A(1; 4) và các đỉnh B, D thuộc đường thẳng [TEX]d: x-2y+2=0.[/TEX] Tìm tọa độ đỉnh B
K
keosuabeo_93
Trong mặt phẳng với hệ tọa độ Oxy, lập pt đường tròn C ngoại tiếp tam giác ABC,biết trực tâm cua tam giác là H(2,10).pt cạnh BC: x+2y-7=0.tâm đg tròn (C) nằm trên đt: x-y-3=0 đồng thời bán kính (c)=5.
K
keosuabeo_93
lập pt đt AC vuông góc vs BD và đi qua A
I là giao của 2 đg chéo AC,BD.
tham số điểm B( B thuộc BD)==>GPT :BI.AI=0 suy ra B
S
somebody1
2) Trong không gian Oxyz, cho đường thẳng [TEX]d:\frac{x-1}{2}=\frac{y+1}{1}=\frac{z}{2}[/TEX] và [TEX]A(1;-1;1)[/TEX]. Gọi H là hình chiếu vuông góc của A trên d. Tìm tọa độ điểm [TEX]H[/TEX] và viêt pt mặt cầu [TEX](C) [/TEX] tâm A cắt d tại 2 điểm [TEX]B[/TEX] và [TEX]C[/TEX] sao cho tam giác [TEX]ABC[/TEX] vuông cân tại [TEX]A.[/TEX]
Last edited by a moderator:
N
nhoc_maruko9x
Nói qua loa cho bạn vậy :|
Tìm H thì đơn giản rồi. Gọi H theo tham số rồi cho [tex]AH \perp \vec{u}[/tex]. Tìm được rồi thì tính cái AH = ... ra. [tex]\Delta ABC[/tex] vuông cân tại A nên [tex]AB = \sqr{\fr32}AH = R.[/tex]
Biết tâm và R rồi thì viết Pt thui
T
teoke1234
Cho tam giác ABC vuông tại C tâm đường tròn nội tiếp I(1;1) bán kinh đường tròn nội tiếp là 2 tâm đường tròn ngoại tiếp là M(3;2) tìm các đỉnh ABC
R
ryelax
Trích đề dự bị khối B năm 2010
Trong mât phẳng tọa độ Oxy, cho đường tròn (C):
^2+(y+1)^2=16})
, tâm i và điểm A(1+
,1). Chứng minh mọi đường thẳng đi qua A đều cắt (C) tại 2 điểm phân biệt. Viết phương trình đường thẳng d đi qua A và cắt (C) tại 2 điểm B,C sao cho tam giác IBC không có góc tù và có diện tích bằng
Trong mât phẳng tọa độ Oxy, cho đường tròn (C):
Last edited by a moderator:
D
duynhan1
Trích đề dự bị khối B năm 2010
Trong mât phẳng tọa độ Oxy, cho đường tròn (C):, tâm i và điểm A(1+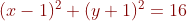
,1). Chứng minh mọi đường thẳng đi qua A đều cắt (C) tại 2 điểm phân biệt. Viết phương trình đường thẳng d đi qua A và cắt (C) tại 2 điểm B,C sao cho tam giác IBC không có góc tù và có diện tích bằng
Hướng giải :
- Chứng minh [TEX]A [/TEX] nằm trong đường tròn (C)
- Kẻ [TEX]IH \bot BC( H \in BC) \Rightarrow IH = \frac{2 S_{IBC}}{2\sqrt{R^2-IH^2}}[/TEX], tính được IH suy ra được pt đường thẳng d và để ý để tam giác ABC không tù thì ta phải có :[TEX]IH > \sqrt{R^2-IH^2}[/SIZE][/FONT][/TEX]