N
nhoc_maruko9x
Mình xin giải theo cách khácMột bài khá hay :
Cho đường tròn [TEX](C): (x-1)^2+(y-2)^2 = 4[/TEX]. Cho điểm [TEX]M(5;3)[/TEX]. Gọi [TEX]T_1, T_2[/TEX] lần lượt là các tiếp điểm kẻ từ M đến (C). Viết phương trình đường thẳng [TEX]T_1 T_2[/TEX].
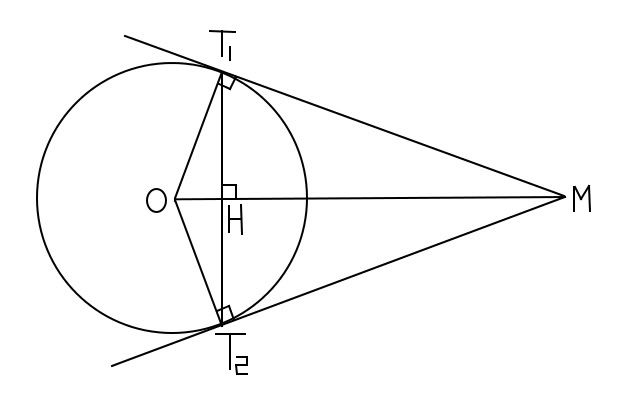
Nhỡ đặt tâm là O rồi, dùng O vậy. Toạ độ là O(1; 2).
Dễ thấy [tex]T_1T_2 \perp OM[/tex] nên [tex]\vec{OM} = (4;1)[/tex] là vecto pháp tuyến của [tex]T_1T_2.[/tex]
[tex]\Delta T_1HM \sim \Delta OT_1M \Rightarrow \fr{T_1M}{HM} = \fr{OM}{T_1M} \Rightarrow T_1M^2 = OM.HM = OM^2 - OT_1^2 \Rightarrow HM = \fr{OM^2-R^2}{OM} = \fr{13}{\sqr{17}}[/tex]
Ta có [tex]\vec{HM} = (5-x;3-y) \Rightarrow HM^2 = (5-x)^2+(3-y)^2 = \fr{169}{17}[/tex]
Một vecto chỉ phương của [tex]T_1T_2[/tex] là [tex]\vec{u} = (1;-4)[/tex]
[tex]\vec{HM} \perp \vec{u} \Rightarrow (5-x)=4(3-y) \Rightarrow 17(3-y)^2 = \fr{169}{17} \Rightarrow (3- y)^2 = \fr{169}{289} \Rightarrow \left\[y = \fr{38}{17}\\y = \fr{64}{17}[/tex]
[tex]\Rightarrow \left\[\vec{HM}=(\fr{33}{17};\tex{ }\fr{13}{17})\\\vec{HM}=(\fr{137}{17};\tex{ }-\fr{13}{17})[/tex]
Vecto đầu tiên nhận vì cùng hướng với [tex]\vec{OM} \Rightarrow T_1T_2:\tex{ }4x+y-10=0[/tex]
Sao ra khác nhóc Ngố nhỷ
Last edited by a moderator:


