L
lamtrang0708
hỏi có bao nhiu cách xếp 4 ng vào 3 lớp biết mỗi lớp có thể chứa đc 4 ng
Last edited by a moderator:
hỏi có bao nhiu cách xếp 4 ng vào 3 lớp biết mỗi lớp có thể chứa đc 4 ng
Giải hệ phương trình:
b)[TEX] \left{\begin{C_x^y-C_x^{y+1}=0}\\{4C_x^y-5C_x^{y-1}=0}[/TEX]
. .[tex]\red \huge Note: \\C_x^a = C_x^b \leftrightarrow \left[ a= b\\ a= x-b[/tex]
Giải hệ phương trình:
a) [TEX]\left{\begin{\frac{A_y^x}{P_{x+1}}+C_y^{y-x}=126}\\{P_{x+1}=720}[/TEX]
Xác định công thức tổng quát của dãy sau :
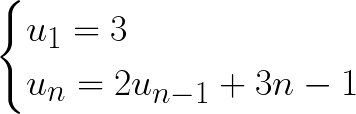
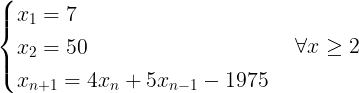
Chứng minh
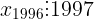
[TEX]C_x^a=C_x^b[/TEX]
\Leftrightarrow [TEX]\left[\begin{a=b}\\{a = x-b} [/TEX]
"Duynhan" ơi,chứng minh hộ công thức này cái
Mình nghĩ: [TEX]C_x^a=C_x^b [/TEX]\Rightarrow [TEX]\left[\begin{a=b}\\{a = x-b} [/TEX]
Chứ tương đương chưa chắc đúng
[TEX]VD: C_4^3[/TEX] và [TEX]C_4^2[/TEX] thì...........đâu có đúng?

Giải thích hộ tớ cái
Tuy bài toán hôm nọ,tớ hỏi cậu có ra đáp án nhưng đấy chỉ là suy luận của cậu
Đã có ai chứng mình công thức mà cậu đưa ra chưa?
Số các số chẵn: d1 = 4x6x5x4tính tổng các số chẵn có 4 c/s phân biệt tạo ra từ các c/s từ 0->6


