D
duynhan1
Bằng quy nạp ta CM được rằng : [TEX]a_n = sin ( \frac{\pi}{2^{n+1}} )[/TEX]
cho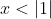
tìm lim của
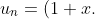(1+x^2)(1+x^4)...(1+x^2^n))
Bằng quy nạp chứ bạn ^^
[tex] \frac{k+1}{2k} . (1- \frac{1}{(k+1)^2} ) = \frac{(k+1).k(k+2)}{2k(k+1)^2} = \frac{k+2}{2(k+1)}[/tex]
Chứng minh rằng [TEX]\forall n \geq2[/TEX], ta luôn có đẳng thức sau:
[TEX](1-\frac{1}{4})(1-\frac{1}{9})...(1-\frac{1}{n^2})=\frac{n+1}{2n}[/TEX]
P/s: giúp mình giải bài này bằng bđt cosi với nhé
[TEX]S_n=\frac{n}{2}(u_n-(n-1)d+u_n)[/TEX]chu vi 1 đa giác là 158
số đo các cạnh của nó lập thành 1 CSC d=3
biết cạnh lớn nhất =44
số cạnh đa giác đó ?
Một bài cực khó( .Sau một đêm trằn trọc suy nghĩ, tìm tòi, học hỏi, cuối cùng thì tớ cũng.....vẫn chưa ra
(
(
(
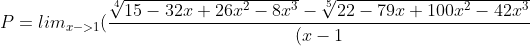%5e2%7d))
Giải pháp tình thế :-s
Xét tính đơn điệu của dãy số [TEX](1+\frac{1}{n})^n[/TEX]
___________________________________
Xét tính đơn điệu của dãy số [TEX](1+\frac{1}{n})^n[/TEX]
___________________________________
cách này cũng nhanh nhỉ
2. Tìm giới hạn
[TEX]a. \lim_{x\to 0} \frac{\sqrt[3]{1+x+x^2}-2x+1}{x}[/TEX]
[TEX]b. \lim_{x\to 5}\frac{\sqrt[3]{3x-7}-x+3}{3-\sqrt{x+4}}[/TEX]
1.CM hàm số [TEX] f(x)=sin{ \frac{1}{\sqrt[3]{x}} }[/TEX] k có giới hạn khi x dần về 0
Điều phải chứng minh tương đương với1.CM hàm số [TEX] f(x)=sin{ \frac{1}{\sqrt[3]{x}} }[/TEX] k có giới hạn khi x dần về 0

Duynhan:Lục lại mấy bài này
1.a. Cho 2 dãy số [TEX](u_n)[/TEX] và [TEX](v_n)[/TEX]. CM nếu [TEX] lim u_n=0[/TEX] và [TEX]lim v_n=0[/TEX] thì [TEX]lim(u_n+v_n)=0[/TEX]
b. Cho 2 dãy số [TEX](u_n)[/TEX] và [TEX](v_n)[/TEX]. CM nếu [TEX]lim u_n=a[/TEX] và [TEX]limv_n=b[/TEX] thì [TEX]lim(u_n+v_n)=a+b[/TEX]
5. /q/<1 và dãy [TEX](u_n)[/TEX] xác định bởi[TEX] u_n=q+2q^2+...+nq^n[/TEX]
Tìm [TEX]lim u_n[/TEX]
tìm lim
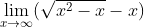
Cũng hơi khó nhai :-w
Khó nhai gì nhỉ :-?
Còn tiến tới [TEX]{-\infty[/TEX]như bạn ghi lúc đầu thì rõ ràng lim= dương vô cùng
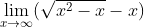
[TEX]= \frac{-x}{\sqrt{x^2-x}+x} = \frac{-1}{1+1}= \frac{-1}{2}[/TEX]
Âm vô cùng thì cái lim tiến tới dương vô cùng /
Đề cậu tự bịa thì có :|

