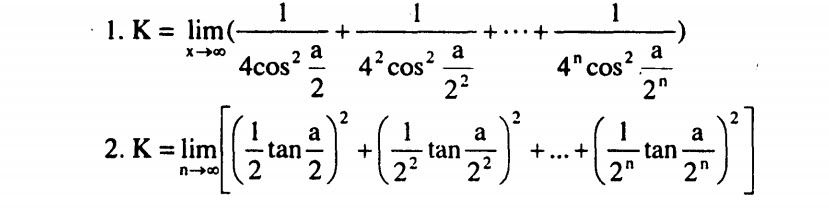L
longt
Cho dãy số (Un) xác định bởi [TEX]\left{ u_1 = 1 \\ u_{n+1} = \frac{(n+2).u_n}{2n} \forall n \ge 1[/TEX]
a) Chứng minh:
Un= n(n+1)/2^n , với mọi n>=1
b) Xét tính đơn điệu và bị chặn của dãy số (Un)
a) Chứng minh:
Un= n(n+1)/2^n , với mọi n>=1
b) Xét tính đơn điệu và bị chặn của dãy số (Un)
Last edited by a moderator: