Toán [Chuyên đề 4] Tổ hợp, dãy số!!

T

thuwshai

duynhan1 said:


Áp dụng :
Có bao nhiêu số tự nhiên gồm bốn chữ số và chia hết cho ít nhất một trong ba số 2,3,5?.

Số các số có 4 chữ số chia hết cho 2: [TEX]\frac{9998-1000}{2}+1 =4500[/TEX]
Số các số có 4 chữ số chia hết cho 3: [TEX]\frac{9999-1002}{3}+1 = 3000[/TEX]
Số các số có 4 chữ số chia hết cho 5: [TEX]\frac{9995-1000}{5}+1 = 1800[/TEX]

Số các số có 4 chữ số chia hết cho 2 và 3 ( tức 6) [TEX]\frac{9996-1002}{6}+1=1500[/TEX]
Số các số có 4 chữ số chia hết cho 3 và 5 ( tức 15) [TEX]\frac{9990-1005}{15}+1=600[/TEX]
Số các số có 4 chữ số chia hết cho 2 và 5(tức 10) [TEX]\frac{9990-1000}{10}+1 =900 [/TEX]

Số các số có 4 chữ số chia hết cho 2 và 3 và 5 : [TEX] \frac{9990-1020}{30}+1=300[/TEX]

Vậy có tổng cộng : [TEX]4500+3000+1800-1500-600-900+300=6600[/TEX]
Bấm để xem đầy đủ nội dung ...
em không hiểu bài này anh giải thích choe m tí được không ạ
tại sao lại chia hết cho 2 thì có : [TEX]\frac{9998-1000}{2}+1 =4500[/TEX]

chia hết cho 3 thì có [TEX]\frac{9999-1002}{3}+1 = 3000[/TEX] và cả những cái đằng sau nữa ạ
:-??
 
D

duynhan1

thuwshai said:
em không hiểu bài này anh giải thích choe m tí được không ạ
tại sao lại chia hết cho 2 thì có : [TEX]\frac{9998-1000}{2}+1 =4500[/TEX]

chia hết cho 3 thì có [TEX]\frac{9999-1002}{3}+1 = 3000[/TEX] và cả những cái đằng sau nữa ạ
:-??
Bấm để xem đầy đủ nội dung ...
Cái ni học lớp 5 rồi mà em. Muốn tìm số số hạng ta lấy số cuối trừ số đầu chia cho khoảng cách rồi cộng cho 1.
;))
Không thì em xem phần cấp số cộng trong sách 11 ý.
 
M

minntuan_94

duynhan1 said:
Ta sẽ đi qua dạng mới, và giải bài toán khá nổi tiếng " Dãy số Fibonacci"
Xác định CT tổng quát của dãy số được xác định bởi :
[TEX]\huge \left{ u_0 = 1 \\ u_1 = 1 \\ u_n= u_{n-1} + u_{n-2} \ \ \forall n \ge 2 [/TEX]

Khó hơn ;))Xác định CT tổng quát của dãy số được xác định bởi :
[TEX]\huge \left{ u_0 = -1 \\ u_1 = 3 \\ u_n-5.u_{n-1} + 6u_{n-2}= 2n^2 + 2n + 1 \ \ \forall n \ge 2 [/TEX]
Bấm để xem đầy đủ nội dung ...
ta có

[TEX] U_n- 2.U_{n-1} -\frac{5}{2}.(2n^2+2n+1)= 3( U_{n-1} - 2U_{n-2}- \frac{5}{2}.(2(n-1)^2+2(n-1)+1) [/TEX]

sau đó dặt [TEX]U_n- 2.U_{n-1} -\frac{5}{2}.(2n^2+2n+1) =V_n[/TEX]

[TEX]\Rightarrow [/TEX] [TEX] V_1=\frac{-27}{2}[/TEX]

suy ra công thức tổng quát của dãy số là [TEX] V_n= 3. (\frac{-27}{2})^{n-1) [/TEX]
thế dúng không anh duynhan
 
K

kysybongma

Giúp mình bài này với :

Trong (mp) cho đa giác đều 2n đỉnh (n là số nguyên dương lớn hơn 1 ) .Hỏi có bao nhiêu hình chứ nhật với các đỉnh là đỉnh của đa giác !
 
K

kysybongma

Giúp mình bài này với :

Trong (mp) cho đa giác đều 2n đỉnh (n là số nguyên dương lớn hơn 1 ) .Hỏi có bao nhiêu hình chứ nhật với các đỉnh là đỉnh của đa giác !
 
Y

yun_lover94

giúp mình bài này nha các bạn:tìm n biết hệ số của x^5 trong khai triển [TEX]({1+{x}^{2}+{x}^{3}})^{n}[/TEX] là 42.tks nhiều!!!!!
 
K

kysybongma

yun_lover94 said:
giúp mình bài này nha các bạn:tìm n biết hệ số của x^5 trong khai triển [TEX]({1+{x}^{2}+{x}^{3}})^{n}[/TEX] là 42.tks nhiều!!!!!
Bấm để xem đầy đủ nội dung ...


[TEX](1+x^2(1+x))^n[/TEX] Có số hạng tổng quát là

[TEX]C_n^kC_k^i x^{2k+i}[/TEX]

Ta có [TEX]2k+i=5[/TEX] ; 0\leqi\leqk\leqn

Ta chỉ có cặp số phù hợp ĐK trên là k=2 ; i=1

Thay vào ta có :

[TEX]C_n^kC_k^i=C_n^2C_2^1=42[/TEX]

\Leftrightarrow[TEX]C_n^2=21[/TEX] \Rightarrow [TEX]n=7[/TEX]
 
G

g4methu123

Mọi người cho em hỏi bài này :(
Em không bik viết công thức nên mọi người chịu khó nhé
Tính tổng
S=C(0,8)C(8,12) + C(1,8)C(7,12) + C(2,8)C(6,12) +...+ C(8,8)C(0,12)
 
H

haojej

duynhan1 said:
Ta nhóm 4 người đó vào 1 nhóm. Cần sắp chỗ ngồi cho nhóm đó và 5 người còn lại có [TEX]\huge 6! [/TEX] cách.
Sắp xếp vị trí của 4 người đó trong nhóm có [TEX]\huge 4! [/TEX] cách.
Vậy tổng cộng có : [TEX] \huge 6!. 4! = 17 280[/TEX] cách.

b) Sắp xếp 9 người đó ngồi tùy ý thì có :

[TEX]\huge 9![/TEX] cách.

Sắp 2 người đó ngồi cùng với nhau thì tương tự câu a ta có :

[TEX]\huge 8!.2![/TEX] cách.

Vậy số cách xếp sao cho 2 người đó ko ngồi cùng với nhau là : [TEX]\huge 282240[/TEX] cách.
Bấm để xem đầy đủ nội dung ...
Bạn quên chưa sắp xếp cho 5 người rồi.Phải nhân thêm với 5! NỮA.
 
H

haojej

duynhan1 said:
Ta nhóm 4 người đó vào 1 nhóm. Cần sắp chỗ ngồi cho nhóm đó và 5 người còn lại có [TEX]\huge 6! [/TEX] cách.
Sắp xếp vị trí của 4 người đó trong nhóm có [TEX]\huge 4! [/TEX] cách.
Vậy tổng cộng có : [TEX] \huge 6!. 4! = 17 280[/TEX] cách.

b) Sắp xếp 9 người đó ngồi tùy ý thì có :

[TEX]\huge 9![/TEX] cách.

Sắp 2 người đó ngồi cùng với nhau thì tương tự câu a ta có :

[TEX]\huge 8!.2![/TEX] cách.

Vậy số cách xếp sao cho 2 người đó ko ngồi cùng với nhau là : [TEX]\huge 282240[/TEX] cách.
Bấm để xem đầy đủ nội dung ...
xIN LỖI MÌNH NHẦM srrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrr
 
T

tuananhbn96

Làm giúp mình bài này với:
Cho 4 số a b 1 2 từng đôi 1 khác nhau! biết rằng viết được 18 chữ số có 3 chữ số khác nhau.! Tìm a b sao cho tổng của 18 số đó bằng 6440
 
P

prince_alone_inlove

18 hay 48 bạn ơi
18 thì sai đề đó
nếu là 48 thì a hoặc b = 0
số còn lại là 2 => sai
kiem tra đề đi bạn
 
Last edited by a moderator:
P

phanvan4

giúp em với

3/ từ 8 chữ số 0,1,2,3,4,5,6,7 có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau và chia hết cho 10
4/ từ 5 chữ số 0,1,2,3,4 lập được bao nhiêu số tự nhiên gồm 3 chữ số khác nhau ? tìm tổng của các số đó
5/ từ 3 số 1,2,3 lập được bao nhiêu số tự nhiên có 4 chữ số trong đó có 2 chữ số 1, 1 chữ số 2, 1 chữ số 3
 
C

cobehophung

bài 1: có 2010 điểm trên mặt phẳng trong đó có 100 điểm thẳng hàng, số còn lại k có 3 điểm nào thẳng hàng. nối 2010 điểm đó với nhau hỏi:
a, có bao nhiêu đường thẳng tạo thành
b. có bao nhiêu tam giác tạo thành
Bài 2:
có 5 cuốn sách toán gióng nhau, 7 cuốn sách lí giống nhau, 8 cuốn sah hóa giống nhau. Đem làm giải thưởng cho 10 hs. mỗi bạn nhân được quyển sách khác loại. hỏi cóa bao nhiêu cách nhận thưởng cho 10 hs trên.
Bài 3:
trong mặt phẳng cho đa giác đều H có 10 cạnh, xét các tam giác được lấy từ các đỉnh của H
a, có bnhieu tam giac như thế có đúng 2 cạnh là cạnh của H
b, _______________________________1________________
c,________________________không có cạnh nào là cạnh của H
 
N

ngongnho

Ta nhóm 4 người đó vào 1 nhóm. Cần sắp chỗ ngồi cho nhóm đó và 5 người còn lại có [TEX]\huge 6! [/TEX] cách.
Sắp xếp vị trí của 4 người đó trong nhóm có [TEX]\huge 4! [/TEX] cách.
Vậy tổng cộng có : [TEX] \huge 6!. 4! = 17 280[/TEX] cách.

b) Sắp xếp 9 người đó ngồi tùy ý thì có :

[TEX]\huge 9![/TEX] cách.

Sắp 2 người đó ngồi cùng với nhau thì tương tự câu a ta có :

[TEX]\huge 8!.2![/TEX] cách.

Vậy số cách xếp sao cho 2 người đó ko ngồi cùng với nhau là : [TEX]\huge 282240[/TEX] cách.[/QUOTE]
 
V

vominhtuan1997

bạn gì đó ơi

herrycuong_boy94 said:
gif.latex


xét phương trinh thứ nhất, ta có
gif.latex

áp dụng công thức để khai triển, ta đươc :
gif.latex


xét phương trình 2 :
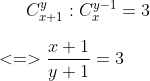
gif.latex


giải tiếp... :D
Bấm để xem đầy đủ nội dung ...

pt 1 thi đúng rồi, còn pt 2 mình thấy là (x+1)/y=3 mới đúng chứ
 
You must log in or register to reply here.
Top Bottom