Q
quyenuy0241
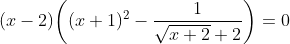
đúng vì
Em chẳng có cách nào thông minh cả :-s, cứ gặp PT là liên hợp
Hô hô lại 1 người nữa phát biểu liều [tex]x \ge 3[/tex] ở đâu đấy!??
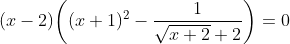
đúng vì
Em chẳng có cách nào thông minh cả :-s, cứ gặp PT là liên hợp
ĐK:-\sqrt3 =<x<=0hoặc [TEX]x>=\sqrt3[/TEX]giải PT:
[tex]1. x^3-3x=\sqrt{x+2} [/tex]
Cách 1Hô hô đặt vô căn cứ . Giải thích coi!
giải PT:
[tex]1. x^3-3x=\sqrt{x+2} [/QUOTE] ĐK[tex] x \geq -2[/tex]
Xét [tex]x>2 [/tex]thì
[tex]x^3-4x=x(x-2)(x+2) >0=>x^3-3x > x[/tex]
mà [tex]x > \sqrt{x+2}[/tex]
[tex]=> VT >VP[/tex]
Xét [tex]-2 \le x \le 2[/tex]
Đặt [tex]x=2cosa[/tex] với a thuoc [tex][0,\pi][/tex]pt có dạng :
[tex]2cos3a=2|cosa|[/tex]
Đến đây dễ rồi
ko hiểu nổi.từ cái chỗ đó sao bạn ko suy ra luôn [TEX]x [/TEX]đita lại có [tex]x^2=x+2[/TEX]
Tìm điều kiện a và b đê hàm số:[TEX]y=asinx+bcosx+2x[/TEX] đông biến trên R
Không tồn tại dấu bằng hả cậu??????????.......................tính đạo hàm

ĐK:-\sqrt3 =<x<=0hoặc [TEX]x>=\sqrt3[/TEX]
[TEX]x^3-3x=\sqrt{x+2}[/TEX]
--->[TEX](x+2)(x-1)^2-\sqrt{x+2}-2=0[/TEX]
coi [TEX]\sqrt{x+2} [/TEX]là ẩn
--->[TEX]\sqrt{x+2}=\frac{1+\sqrt{1+8(x-1)^2}}{2(x-1)^2}[/TEX]
---->[TEX]\sqrt{3+(x-1)}=\frac{1+\sqrt{1+8(x-1)^2}}{2(x-1)^2}[/TEX]
VT đồng biến
xét VP:chú ý phải xét 2khoảng riêng rẽ,ko được xét gộp
với -\sqrt3 \leqx \leq0--->tập giá trị của VT và VP ko có phần chung
----->ko có nghiệm thuộc khoảng này
với [TEX]x\geq\sqrt3[/TEX]--->VP nghịch biến
-->pt có nhiều nhất 1 nghiệm thuộc khoảng này
mà [TEX]x=2[/TEX]là nghiệm
vậy pt có nghiệm duy nhất [TEX]x=2[/TEX]
[TEX]\sqrt{\sqrt{3}-x}=x\sqrt{\sqrt{3}+ x}[/TEX]
Vì để bình phương 2 vế thì cần đk để 2 vế dương[TEX]\sqrt{\sqrt{3}-x}=x\sqrt{\sqrt{3}+ x}[/TEX]
[TEX]\Leftrightarrow \sqrt{3}-x=x^2(\sqrt{3}+x)[/TEX]
[TEX]\Leftrightarrow (x+1)[x^2+x(\sqrt{3}-1)-\sqrt{3}+1]=0[/TEX]
[TEX]\Rightarrow ...[/TEX]
nhưng sao -1 hk phải nghiệm pt
Thử làm thế này: (nhưng mà cách này cứ thấy nó *** ý)[TEX]\sqrt{\sqrt{3}-x}=x\sqrt{\sqrt{3}+ x}[/TEX]
Thử làm thế này: (nhưng mà cách này cứ thấy nó *** ý)
Từ đề bài \Rightarrow x>0, x# [TEX]\sqrt{3}[/TEX]
\Rightarrow[TEX]\sqrt{3}-x<\sqrt{3}+x \\ \Rightarrow \sqrt{\sqrt{3}-x}<\sqrt{\sqrt{3}+x} \\ \Rightarrow\sqrt{\sqrt{3}-x}< x\sqrt{\sqrt{3}+ x}[/TEX]
\RightarrowPt vô nghiệm

