Z
zero_flyer
Trường hợp cosx=0 đâu mất rồi ^ ^
éc hok cẩn thận, cảm ơn anh minh, chừa rồi, do làm dạng này cứ thấy cos luôn khác 0 nên... hok để ý
Trường hợp cosx=0 đâu mất rồi ^ ^
bài
giải phương trình lượng giác àh:
chia hai vế cho cos^3x
[tex]tan^3x-1=tanx(tan^2x+1)+tan^2x+1[/tex]
[tex]tan^2x+tanx+2=0[/tex]
hình như là vô nghiệm, ^^
bài
này ko vô nghệm đâu.................................
mình gợi ý làm theo PT tích
bài này của ông hay đấy( lần sau post thêm vài bài nữa nha vì tôi ko có quyển nào về phần giải PT)Hệ phương trình mới
[TEX]\left{\begin{x^2+2x^2y^2=5y^2-y^4}\\{x-xy+x^2y=y-y^2}[/TEX]
mọi người coi lại bài này hộ Oack cái ^^Từ pt 2 ---> xy = [TEX]\frac{6x +6 - x^2}{2}[/TEX]
pt 1 <---> [TEX] (x^{2} + xy )^2 =2x+9[/TEX]
<--> [TEX]x^{2} + \frac{6x +6 - x^2}{2}= 2x+9[/TEX]
[TEX]<--->( x^{2} +6x+6)^2[/TEX] = 8x +36
<--->[TEX] x^4 + 12x^3 + 48x^2 +64x = 0[/TEX]
<--> x = 0 loại
hoặc x = -4 ---> y= [TEX]\frac {17}{4}[/TEX]
1. Với giá trị nào của [TEX]m[/TEX] thì;
[TEX](\frac 15) ^{|x^2-4x+3|}=m^4-m^2+1[/TEX] có 4 nghiệm phân biệt
cách của bạn đi thi đại học ko dùng được đâuXét hàm số : [TEX]y=\(x-1)^{2009}+(2-x)^{2009}[/TEX]
[TEX]MXD:D=R[/TEX]
Đạo hàm .
[TEX]y'=2009\[\(x-1\)^{2008}-\(2-x\)^{2008}\][/TEX]
[TEX]y'=0\Leftrightarrow x=\frac{3}{2}[/TEX] [TEX]Duy nhat[/TEX]
Vậy theo [TEX]Roll[/TEX] phương trình [TEX](x-1)^{2009}+(2-x)^{2009}=1[/TEX] có tối đa hai nghiệm.
Nhẫm nghiệm ta thấy [TEX]\left[x=1\\x=2[/TEX]
______
khanhsy
2) [TEX]\left{\begin{(x^2+y)(xy+1)+xy=-\frac{5}{4}}\\{(x^2+y)^2+xy=-\frac{5}{4}} [/TEX]Bài 1: đề thi đại học khố B-2008.bài này post rồi nhưng ai có cách giải khác nhanh hơn của Quynhdihoc ko? cách của tớ cũng dài lắm.
Bài 2:đề thi đại học khối A-2008
[tex]\left{x^2+y+x^3y+xy^2+xy=\frac{-5}{4}\\x^4+y^2+xy(1+2x)=\frac{-5}{4}[/tex]
tìm [TEX]m[/TEX] để hệ sau có nghiệm :
[TEX]\red \left{x^2-3x-4 \leq 0\\x^3-3|x|.x-m^2-15m \geq 0[/TEX]
giả sử [TEX]x[/TEX] \geq [TEX]y[/TEX] \geq [TEX]z[/TEX] [TEX](1)[/TEX]Giải hệ pt này: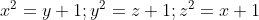
[tex]\left{y^3-9x^2+27x-27=0\\z^3-9y^2+27y-27=0\\x^3-9z^2+27z-27=0[/tex]
làm tạm bài này đã
hiz thi học kì xong sẽ vào topic này nhi êù

