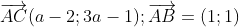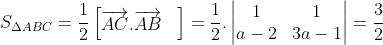Tổng kết các kết quả của đề số 18
Mai(canmongtay):
Câu 1:
Phương trình hoành độ giao điểm của 2 đường là
x^3+3x^2+mx+1=1
[TEX]\Leftrightarrow x(x^2+3x+m)=0[/TEX]
[TEX]\Leftrightarrow x=0 hay x^2+3x+m=0[/TEX](*)
(Cm) cắt dt y=1 tại C(0,1), D,E phân biệt thì
pt(*) phải có 2 nghiệm phân biệt xD, xE #0
<...> delta >0 và f(0)#0
<....> m#0 và m< 9/4(1)
Khi đó tiếp tuyến tại D,E có hệ số góc lần lượt là
kD=y'(xD)=3xD^2+6xD+m=-(3xD+2m)
kE=y'(xE)=3xE^2+6xE+m=-(3xE+2m)
Các tiếp tuyến tại D và E vg vs nhau khi và chỉ khi
kD.kE=-1
[TEX]\Leftrightarrow (3xD+2m)(3xE+2m)=-1[/TEX]
<....>9xDxE+6m(xD+xE)+4m^2=-1
<.....>9m+6m(-3)+4m^2=-1
<......>4m^2-9m+1=0
<......>[TEX]m= \frac{9+\sqrt{65}}{8} + m= \frac{9- \sqrt{65}}{8} [/TEX](2)
từ(1)+(2)....> nghiêm m như trên thỏa mãn đề bài
Câu V2: (ngocthao1995)
M thuộc d -->[TEX] M(1-t,-2+t,2t)[/TEX]
[TEX]MA^2+MB^2=28[/TEX]
[TEX]\Leftrightarrow t^2+(6-t)^2+(2-2t)^2+(-2+t)^2+(4-t)^2+(4-2t)^2=28[/TEX]
[TEX]\Leftrightarrow 12t^2-48t+48=0[/TEX]
[TEX]\Leftrightarrow t=2[/TEX]
[TEX]\Leftrightarrow M(-1,0,4)[/TEX]
Bài 2: Tears!!!!(passingby)
[TEX] I = \int_{0}^{\frac{\pi}4}(x+ sin^22x)cos2xdx[/TEX]
\Leftrightarrow[TEX]I=\int_{}^{}xcos2xdx + \int_{}^{}cos2xsin^2{2x}dx[/TEX]
\Leftrightarrow[TEX]I=\int_{}^{}xcos2xdx +\int_{}^{}sin^2{2x}d(sin2x)[/TEX]
\Leftrightarrow[TEX]I=\int_{}^{}xcos2xdx + \frac{sin^3{2x}}{3}[/TEX]
Tính [TEX]I1=\int_{}^{}xcos2xdx [/TEX]
Đặt [TEX]u=x \Leftrightarrow du=dx[/TEX]
[TEX]dv=cos2xdx \Leftrightarrow v =\frac{sin2x}{2}[/TEX]
\Rightarrow[TEX]I1=\frac{xsin2x}{2} - \frac{1}{2}\int_{}^{}sin2xdx[/TEX]
\Leftrightarrow[TEX]I1=\frac{xsin2x}{2} - \frac{cos2x}{4}[/TEX]
............
(đang thế cận =)) )
Xong 
[TEX]I=\frac{7}{12} + \frac{pi}{4}[/TEX]
Câu II1: duynhan1
Điều kiện: [TEX] x\ge 1 \ \ , y \ge \frac12[/TEX]
[TEX](1) \Leftrightarrow (\sqrt{x} + \sqrt{y})( \sqrt{x} - 2 \sqrt{y}) = 0 \\ \Leftrightarrow x= 4y[/TEX]
Thế vào (2).
Bên TOPIC cũ có rồi!
Bài bất đẳng thức (Miko........)
ta có cần chứng minh cho
[TEX]\Leftrightarrow \frac{a+b^2}{b+c}+1+ \frac{b+c^2}{a+c}+1+\frac{c+a^2}{a+b}+1 \geq 5 [/TEX]
[TEX] \Leftrightarrow \frac{1+b^2}{b+c}+ \frac{1+c^2}{a+c}+\frac{1+a^2}{a+b}\geq5[/TEX]
Mà
[TEX] \frac{1}{b+c}+\frac{1}{b+a}+ \frac{1}{a+c} \geq \frac{9}{2}[/TEX]
và
[TEX] \frac{b^2}{b+c}+\frac{a^2}{b+a}+ \frac{c^2}{a+c} \geq \frac{1}{2}[/TEX]
=> đpcm
dấu = xảy ra khi và chỉ khi[TEX] a=b=c[/TEX]
kira_l làm những câu sau:
Câu VI [/U]: Gải BPT [TEX](2+\sqrt{3})^{x^2 -2x+1} + (2-\sqrt{3})^{x^2-2x-1} \leq \frac{4}{2-\sqrt{3}}[/TEX]
[/B]
[TEX]\Leftrightarrow (2+\sqrt{3}).(2+\sqrt{3})^{x^2-2x} + \frac{(2-\sqrt{3})^{x^2-2x}}{2-\sqrt3} \leq \frac{4}{2-\sqrt3}[/TEX]
[TEX]\Leftrightarrow (2+\sqrt{3})^{x^2 -2x} + (2-\sqrt{3})^{x^2-2x} \leq 4 (1)[/TEX]
Nhận thấy [TEX](2+\sqrt3).(2-\sqrt3)=1 \Rightarrow (2+\sqrt{3})^{x^2 -2x} = t (t>0) thi` (2-\sqrt{3})^{x^2-2x} = \frac{1}{t}[/TEX]
[TEX](1) \Leftrightarrow t + \frac{1}{t} \leq 4[/TEX]
[TEX]\Leftrightarrow t^2 - 4t + 1\leq 4 (cause : t>0)[/TEX]
[TEX]\Leftrightarrow 2-\sqrt3 \leq t \leq 2+\sqrt3[/TEX]
[TEX]\Rightarrow 2-\sqrt3 \leq (2-\sqrt3)^{x^2-2x} \leq 2+\sqrt3[/TEX]
[TEX]\Leftrightarrow -1 \leq x^2 - 2x \leq 1[/TEX]
[TEX]\Leftrightarrow 1 - \sqrt2 < x \leq 1+\sqrt2[/TEX]
Câu III
1. Trên cạnh AD của hình vuông ABCD có độ dài a , lấy M sao cho AM = x ( 0<x<a)
Trên đt vuông góc với (ABCD) tại A lấy S sao cho SA = 2a.
a,Tính kc từ M đến (SAC)
b, Kẻ MH vuông góc với AC tại H.Timg vị trí của M để V chóp SMCH max
[TEX]a/[/TEX]
[TEX]S_{\triangle{AMC}} = \frac{1}{2}.AM.CD = \frac{ax}{2}[/TEX]
[TEX]\Rightarrow V_{S.ACM} = \frac{1}{3}.SA.S_{\triangle{AMC}} = \frac{a^3x}{3}[/TEX]
Lại có:
[TEX]S_{\triangle{SAC}} = \frac{1}{2}.SA.AC = \frac{1}{2}. 2a. a\sqrt2 = a^2\sqrt2[/TEX]
[TEX]\Rightarrow d(M,(SAC))= \frac{3V_{S.ACM}}{S_{\triangle{SAC}}} = \frac{x\sqrt2}{2}[/TEX]
Câu V:[/B]
Câu V.
1.Trong mp Oxy cho tam giác ABC biết A (2;-3) , B (3;-2) có S = 3/2 và trọng tâm thuộc đt (d) : 3x - y - 8 = 0.Tìm C.
Chúc mọi ng năm mới vui vẻ. Thi đỗ đại học hết nhá.
[/QUOTE]
Câu V , đề 16 (Hoanghondo94) :">: (Mọi người làm hết rồi ,..còn câu cuối hic.........)
Gọi [TEX]{\color{Blue} G(a;3a-8)[/TEX] là trọng tâm của tam giác ở trên [TEX]{\color{Blue} (d)[/TEX]
Phương trình đường thẳng [TEX]{\color{Blue} AB: x-y-5=0[/TEX] , độ dài cạnh AB là : [TEX]{\color{Blue} AB=\sqrt{2}[/TEX]
Chiều cao h của tam giác ABC xuất phát từ đỉnh C là : [TEX]{\color{Blue} h=\frac{2S}{AB}=\frac{3}{\sqrt{2}}[/TEX]
Khoảng cách từ G đến AB bằng [TEX]{\color{Blue} \frac{1}{3}[/TEX] chiều cao :
[TEX]{\color{Blue} \frac{1}{3}.\frac{3}{\sqrt{2}}=\frac{|a-(3a-8)-5|}{\sqrt{2}}\Leftrightarrow |2a-3|=1\Leftrightarrow \[a=2 \\ a=1[/TEX]
Ta được 2 điểm [TEX]{\color{Blue} G(2;-2) \ va \ G(1;-5)[/TEX]
-Với [TEX]{\color{Blue} G(2;-2)[/TEX] ta có :
[TEX]{\color{Blue} \[x_C=3x_G-x_A-x_B=1 \\ y_C =3y_G- y_A-y_B=-1 \Rightarrow C(1;-1)[/TEX]
-Tương tự [TEX]{\color{Blue} G(1;-5)\Rightarrow C(-2;-10)[/TEX]
Câu IIIb:
Làm câu b không được thì xử câu a vậy :">
b. Dễ thấy OD vuông góc mp (SAC) nên OD chính là khoảng cách từ D đến mp (SAC)
Mặt khác
[TEX]\frac{d(M;(SAC))}{d(D;(SAC))} = \frac{AM}{AD} = \frac{MH}{DO}= \frac{x}{a} [/TEX]
[TEX]\Rightarrow d(M;(SAC)) = MH = OD.\frac{x}{a} = \frac{x\sqrt2}2[/TEX]
Câu II: (lc.....)
ĐK:
PT
đặt nhân tử chung: pt
tới đây cosx- sinx=0 thì dể phải không các bạn.
còn vế thứ hai ta quy đồng và dùng công thức hạ bậc ta được:
rỏ ràng pt này vô nghiệm các bạn hì.
vậy ta có: tan(x)=1 thỏa ĐK và x thuộc (0,pi) nên: