A
asroma11235
1)tìm tất cả các nghiệm nguyên của phương trình:
a)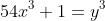
b)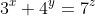
)
_Nếu x=1 thì y không được nguyên cho lắm[TEX]\Leftrightarrow (y-1)(y^2+y+1)=54x^3[/TEX]
[TEX]\Rightarrow y=3k+1[/TEX]
[TEX]\Rightarrow 9k(3k^2+3k+1)=54x^3[/TEX]
[TEX]\Rightarrow k=0, x=1[/TEX]

Kết quả sai rồi =,=!
Last edited by a moderator:

