V
vuanoidoi
nhân ra làm j` hả bạncách hay nhất là nhân bổ ra
bài này chỉ 2 dòng thôi
@019549009:cái dòng chữ kí của e nghĩa là j` vậy :-SSphang toàn TA
bài này chỉ 2 dòng thôi
@019549009:cái dòng chữ kí của e nghĩa là j` vậy :-SSphang toàn TA
0
0915549009
Bài đó chak các bạn đã làm ra, ai làm xong thỳ post bài giải lên nhaz
Tiện thể mọi người chém típ 2 bài hén)))
* Vs các a, b, c dương. CM các BĐT sau:
[TEX]1)\frac{ \sum ab}{\sum a^2} + \frac{ (\sum a)^3}{abc} \geq 28[/TEX]
[TEX]2) \sum\frac{5b^3-a^3}{ab+3b^2} \leq \sum a[/TEX]
Tiện thể mọi người chém típ 2 bài hén
)))* Vs các a, b, c dương. CM các BĐT sau:
[TEX]1)\frac{ \sum ab}{\sum a^2} + \frac{ (\sum a)^3}{abc} \geq 28[/TEX]
[TEX]2) \sum\frac{5b^3-a^3}{ab+3b^2} \leq \sum a[/TEX]
Last edited by a moderator:
T
tell_me_goobye
Hix, nói dzậy mà pic vẫn ế
Cống hiến cho nền văn minh nhân loại một bài dzậy
Bài cực dễ
Cho a, b, c dương. CMR: [TEX](1+a^3)(1+b^3)(1+c^3)\geq (1+ab^2)(1+bc^2)(1+ca^2)[/TEX]
P/s: Các mem trên lớp 8 là ko đc làm nhaz
bài dễ chưa từng có
holder
[TEX](1+a^3)(1+b^3)(1+b^3) \geq (1+ab^2)^3 [/TEX]
ok hoàn tất
V
vuanoidoi
L
legendismine
Làm 2 dòng đi bạn tớ xem nào xin chỉ giáonhân ra làm j` hả bạn
bài này chỉ 2 dòng thôi
@019549009:cái dòng chữ kí của e nghĩa là j` vậy :-SSphang toàn TA
0
0915549009
Chính xác là ko phải 2 dòng mà là 4 dòng (nếu trình bày đầy đủ) =))=))=))
Theo BĐT Holder thỳ:
[TEX](1+a^3)(1+b^3)(1+b^3)\geq (1+ab^2)^3[/TEX]
[TEX](1+a^3)(1+a^3)(1+c^3)\geq (1+a^2c)^3[/TEX]
[TEX](1+c^3)(1+c^3)(1+b^3)\geq (1+bc^2)^3[/TEX]
[TEX]\Rightarrow (1+ab^2)^3(1+bc^2)^3(1+ca^2)^3 \leq (1+a^3)^3(1+b^3)^3(1+c^3)^3\ \Rightarrow dpcm[/TEX]
P/s: A tell đừng bảo e ăp cắp bản quyền nhaz
Theo BĐT Holder thỳ:
[TEX](1+a^3)(1+b^3)(1+b^3)\geq (1+ab^2)^3[/TEX]
[TEX](1+a^3)(1+a^3)(1+c^3)\geq (1+a^2c)^3[/TEX]
[TEX](1+c^3)(1+c^3)(1+b^3)\geq (1+bc^2)^3[/TEX]
[TEX]\Rightarrow (1+ab^2)^3(1+bc^2)^3(1+ca^2)^3 \leq (1+a^3)^3(1+b^3)^3(1+c^3)^3\ \Rightarrow dpcm[/TEX]
P/s: A tell đừng bảo e ăp cắp bản quyền nhaz
Last edited by a moderator:
V
vuanoidoi
oàm hoá ra từ nãy đề sai.thảo nào từ náy thay a=b=c vào ko đc /Bài đó chak các bạn đã làm ra, ai làm xong thỳ post bài giải lên nhaz
Tiện thể mọi người chém típ 2 bài hén
* Vs các a, b, c dương. CM các BĐT sau:
[TEX]1)\frac{ \sum ab}{\sum a^2} + \frac{ (\sum a)^3}{abc} \geq 28[/TEX]
[TEX][\frac{ \sum ab}{\sum a^2}-1] + [\frac{ (\sum a)^3}{abc}-27] \geq 0[/TEX]
S.O.S rõ ràng
V
vuanoidoi
mình cũng làm như :tell_me_godbye thôi nhưng dùng CM tương tự chỉ cần 1 dòngLàm 2 dòng đi bạn tớ xem nào
....nhân vào và 1 dấu => là dòng thứ 2
MÀ MÌNH CŨNG HƠI NÓI QUÁ.XIN LỖI CẬU VÀ MỌI NGƯờI
Q
quan8d
Trêbưshev : [TEX]\frac {3\sum a^2}{\sum a} = \frac {3.2\sum a^2}{2\sum a} \geq \sum \frac{a^2+b^2}{a+b}[/TEX]Pic ế, pic ế, post bài gì đi chủ pic ơi, bik là spam nhưng vì quyền lợi chung thui
Thui, post 1 bài "cho có lệ" ko lại bị del bài mất tiêu
CMR:
[TEX] \sum \frac{a^2+b^2}{a+b}\le \frac {3\sum a^2}{\sum a} [/TEX]
T
trydan
0
0915549009
Ôi cái cuộc đời này )))
[TEX]\frac{(a+b)^2}{2} + \frac{a+b}{4}=\frac{a+b}{2}(a+b + \frac{1}{2} ) \geq \sqrt{ab}(a+b + \frac{1}{2}) [/TEX]
Sau đóa xét hiệu
)))[TEX]\frac{(a+b)^2}{2} + \frac{a+b}{4}=\frac{a+b}{2}(a+b + \frac{1}{2} ) \geq \sqrt{ab}(a+b + \frac{1}{2}) [/TEX]
Sau đóa xét hiệu
Last edited by a moderator:
Q
quan8d
T
trydan
Q
quyenuy0241
Chovà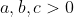
Chứng minh rằng
[tex]\frac{1}{a^2+2b^2+3} \le \frac{1}{2(ab+b+1)} [/tex]
Ta luôn có đẳng thức sau với [tex]abc=1[/tex]
[tex]\frac{1}{ab+b+1}+\frac{1}{bc+c+1}+\frac{1}{ac+a+1}=1 [/tex]
:-SS
0
0915549009
Thêm mấy bài nữa nhaz mọi ngừi )). Ko khó lắm
1) CM vs a, b, c dương:
[TEX]\frac{(a+b)^2}{c}+\frac{(b+c)^2}{a}+\frac{(c+a)^2}{b}\geq 4(a+b+c)[/TEX]
2) CMBĐT:
[TEX]\frac{a^3}{b^2-bc+c^2}+\frac{b^3}{c^2-ca+a^2}+\frac{c^3}{a^2-ab+b^2}\geq \frac{3(ab+bc+ca)}{a+b+c}[/TEX]
)). Ko khó lắm 1) CM vs a, b, c dương:
[TEX]\frac{(a+b)^2}{c}+\frac{(b+c)^2}{a}+\frac{(c+a)^2}{b}\geq 4(a+b+c)[/TEX]
2) CMBĐT:
[TEX]\frac{a^3}{b^2-bc+c^2}+\frac{b^3}{c^2-ca+a^2}+\frac{c^3}{a^2-ab+b^2}\geq \frac{3(ab+bc+ca)}{a+b+c}[/TEX]
D
deltano.1
1\THEO SVACXO [TEX] vt\geq\frac{4(a+b+c)^2}{a+b+c}=4(a+b+c)[/TEX]Thêm mấy bài nữa nhaz mọi ngừi
1) CM vs a, b, c dương:
[TEX]\frac{(a+b)^2}{c}+\frac{(b+c)^2}{a}+\frac{(c+a)^2}{b}\geq 4(a+b+c)[/TEX]
2) CMBĐT:
[TEX]\frac{a^3}{b^2-bc+c^2}+\frac{b^3}{c^2-ca+a^2}+\frac{c^3}{a^2-ab+b^2}\geq \frac{3(ab+bc+ca)}{a+b+c}[/TEX]
2\THEO VORNICU-SCHUR VS SVACXO
Last edited by a moderator:
0
01263812493
Mình cần cách giải dễ hiểu mà mới lạ
Cho các số dương a,b,c,d. Chứng minh:
[TEX]\frac{a}{b+c}+\frac{b}{c+d}+\frac{c}{d+a}+\frac{d}{a+b}\geq 2[/TEX]
2.Cho các số dương x,y,z,t có tổng bằng 2. Tìm Min:
[TEX]\frac{(x+y+z)(x+y)}{xyzt}[/TEX]
Cho các số dương a,b,c,d. Chứng minh:
[TEX]\frac{a}{b+c}+\frac{b}{c+d}+\frac{c}{d+a}+\frac{d}{a+b}\geq 2[/TEX]
2.Cho các số dương x,y,z,t có tổng bằng 2. Tìm Min:
[TEX]\frac{(x+y+z)(x+y)}{xyzt}[/TEX]
L
legendismine
Câu 1:Mình cần cách giải dễ hiểu mà mới lạ
Cho các số dương a,b,c,d. Chứng minh:
[TEX]\frac{a}{b+c}+\frac{b}{c+d}+\frac{c}{d+a}+\frac{d}{a+b}\geq 2[/TEX]
2.Cho các số dương x,y,z,t có tổng bằng 2. Tìm Min:
[TEX]\frac{(x+y+z)(x+y)}{xyzt}[/TEX]
Đặt [TEX]S=VT; M=\sum_{cyc}\frac {b}{b+c}; N=\sum_{cyc}\frac {c}{b+c}[/TEX]
Ta có:
[TEX]M+N=4; S+M\ge 4;S+N\ge 4 \Leftrightarrow2S+M+N\ge 8\ =>S\ge 2[/TEX]
T
tell_me_goobye
Q
quyenuy0241
Đang rảnh góp vui cùng các em lớp 8
[tex](x+y+z+t)^2 \ge 4t(x+y+z) [/tex]
[tex](x+y+z)^2 \ge 4z(x+y) [/tex]
[tex](x+y)^2 \ge 4xy [/tex]
Nhân các BDT trên với nhau:
[tex]2.(x+y+z)(x+y) \ge 4^3.xyzt \Rightarrow \frac{(x+y+z)(x+y)}{xyzt} \ge 32[/tex]
Dấu "=" xảy ra:
[tex]x=y=\frac{z}{2}=\frac{t}{4} [/tex]