0
0915549009
Làm theo cách của anh son_9f_ltv hơi khó hiểu(chính xác là em ko hiểu gì cả)dương . Chứng minh rằng: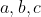

Chứng minh rằng vs mọi x thuộc R thỳ:
[tex](\frac{12}{5})^x + (\frac{15}{4})^x +(\frac{20}{3})^x \geq 3^x+4^x+5^x[/tex]
Bài này ko khó
Last edited by a moderator:

