V
vuanoidoi
BĐT nesbit:::::ChoChứng minh rằng
}+\frac{yz}{x(y+z)}+\frac{zx}{y(z+x)} \geq \frac{3}{2})
[tex] \sum\frac{a}{b+c} \ge \frac{3}{2} [/tex]
BĐT nesbit:::::ChoChứng minh rằng
}+\frac{yz}{x(y+z)}+\frac{zx}{y(z+x)} \geq \frac{3}{2})
bài này cho a,b,c mà chứng minh x,y,zChoChứng minh rằng

Giống bài ở trên thuiChovà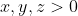 Chứng minh rằng
Chứng minh rằng
}+\frac{1}{x^2(y+z)}+\frac{1}{y^2(z+x)} \geq \frac{3}{2})
Chovà Chứng minh rằng
Chứng minh rằng
}+\frac{b^3}{c(1-c)}+\frac{c^3}{a(1-a)} \geq \frac{1}{2})
[TEX]\sum \frac{1}{x^2(yz+zt+ty)} = \sum \frac{yzt}{xyz+xzt+xty}[/TEX]Chovà Chứng minh rằng
Chứng minh rằng
}+\frac{1}{y^2(xz+zt+tx)})
}+\frac{1}{t^2(xy+yz+zx)} \geq \frac{4}{3})
Trưa nay nghĩ ra rùi nhưng lại phải đi họcChoChứng minh rằng
)
Cuối cùng cũng chém raChovà Chứng minh rằng
Chứng minh rằng
)
chebyshev........................................................................Pic ế, pic ế, post bài gì đi chủ pic ơi, bik là spam nhưng vì quyền lợi chung thui)
)
)
Thui, post 1 bài "cho có lệ" ko lại bị del bài mất tiêu)
)
)
CMR:
[TEX] \sum \frac{a^2+b^2}{a+b}\le \frac {3\sum a^2}{\sum a} [/TEX]
[tex]<=> a^2(b-1)+b^2(c-1)+c^2(a-1)+1 \ge 0[/tex]a,b,c thuộc [0,1]
chứng minh [TEX]a^2+b^2+c^2\leq1+a^2b+b^2c+c^2a[/TEX]
[tex]f(1)=b+b^2(c-1) \ge 0[/tex](***)[tex]<=> a^2(b-1)+b^2(c-1)+c^2(a-1)+1 \ge 0[/tex]
Đặt:[tex] f(a)= a^2(b-1)+b^2(c-1)+c^2(a-1)+1[/tex]
[tex]f(0)=b^2(c-1)-c^2+1[/tex]
[tex]f(1)=b+b^2(c-1) \ge 0[/tex](***)
Đặt:[tex]g(b)=b^2(c-1)-c^2+1[/tex]
[tex]g(0)=1-c^2 \ge 0 [/tex]
[tex]g(1)=c-c^2 \ge 0 [/tex]
[tex]=>g(b) \ge 0 [/tex]
[tex]=>f(0) \ge 0 [/tex](****)
từ (***) vs (****) => đfcm: [tex]f(a) \ge 0 [/tex]
do:[tex]b \in [0,1] [/tex][tex]f(1)=b+b^2(c-1) \ge 0[/tex](***)
\Rightarrow
giải thích giùm chỗ này luôn bạn ơi
Hix, nói dzậy mà pic vẫn ế(
((
Cống hiến cho nền văn minh nhân loại một bài dzậy)
)
)
Bài cực dễ)
)
)
Cho a, b, c dương. CMR: [TEX](1+a^3)(1+b^3)(1+c^3)\geq (1+ab^2)(1+bc^2)(1+ca^2)[/TEX]
P/s: Các mem trên lớp 8 là ko đc làm nhaz

