0
0915549009
Bạn có thể chứng minh dạng tổng quát này đc ko? Còn bài kia thì mình thấy hơi khó hiểuTìm tất cả các sốsao BDT luôn đúng với mọi và
và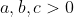 :
: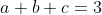

Bài trên là 1 trường hợp đặc biệt với
Bạn có thể chứng minh dạng tổng quát này đc ko? Còn bài kia thì mình thấy hơi khó hiểuTìm tất cả các sốsao BDT luôn đúng với mọi và
và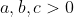 :
: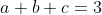

Bài trên là 1 trường hợp đặc biệt với
Tìm tất cả các sốsao BDT luôn đúng với mọi và
và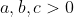 :
: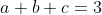

Bài trên là 1 trường hợp đặc biệt với
Cho các số thực dương a,b,c,d thoả mãn :
[TEX]a+b+c+d = a^2+b^2+c^2+d^2[/TEX]
Chứng minh rằng :
[TEX]2(a^3+b^3+c^3+d^3)+a+b+c+d \leq 12[/TEX]
BĐT<=>[tex]a^2b+ab^2+a^2c+ac^2+b^2c+bc^2+2abc+7\geq 5(a+b+c)[/tex]1) Cho a, b, c dương và abc = 1
CMR: [TEX](a+b)(b+c)(c+a)+7\geq 5(a+b+c)[/TEX]
Nếu áp dụng p, q, r thì bạn phân tích ra làm gì cho dài:BĐT<=>[tex]a^2b+ab^2+a^2c+ac^2+b^2c+bc^2+2abc+7\geq 5(a+b+c)[/tex]
<=>[tex](ab+ac+bc)(a+b+c)+6 \geq5(a+b+c)[/tex]
using p,q,r
1) Cho a, b, c dương và abc = 1
CMR: [TEX](a+b)(b+c)(c+a)+7\geq 5(a+b+c)[/TEX]
Mình thấy cách của BigBang195 cho bài giải này hơi khó hiểu theo mình cách này có vẻ dễ hiểu hơn:Chứng minh rằng nếuthì

Chứng minh rằng nếuthì

Làm dzậy làm gì cho dài, mà bài này từ lâu lắm rồi mà,.................... :|:|Mình thấy cách của BigBang195 cho bài giải này hơi khó hiểu theo mình cách này có vẻ dễ hiểu hơn:
Ta có
\frac{x^2}{y^2}+\frac{y^2}{x^2}+2=(\frac{x}{y}+\frac{y}{x}[/IMG])^2
Ta lại có (\frac{x}{y}+\frac{y}{x})^2 - (\frac{x}{y}+\frac{y}{x}) - 2
= (\frac{x}{y}+\frac{y}{x}+1)( \frac{x}{y}+\frac{y}{x} - 2) \geq 0
Vì theo cô-si ta có \frac{x}{y}+\frac{y}{x}\geq 2
Uhm, anh nhầm chút , giải lại nhá)
[tex]a=max{a,b,c}[/tex] đặt b+c=x . chúng ta có [/tex]a \ge 1 , x \ge 2\sqrt{bc}=\frac{2}{\sqrt{a}}[/tex]
Xét
[tex]f(a,b,c)=(a+b)(b+c)(c+a)+7-5(a+b+c)=x(ax+a^2+bc)+7-5(a+x)=ax^2+(a^2+bc-5)x+7-5a= a(x+\frac{a^2+bc-5}{2a})^2-\frac{a^2+bc-5}{4a}+7-5a [/tex]
Lại có [tex]\frac{2}{\sqrt{a}} \ge \frac{2}{a}[/tex]
Xét [tex]x+\frac{a^2+bc-5}{2a} \ge \frac{2}{\sqrt{a}}+\frac{a^2+bc-5}{2a} \ge \frac{2}{a}+\frac{a^2+bc-5}{2a}= \frac{a^2+\frac{1}{a}-1}{2a} >0 [/tex]
Thế [tex]x= \frac{2}{\sqrt{a}}[/tex] vô
[tex]f(a,b,c) \ge 2(a^2+\frac{1}{a}-5)\frac{1}{\sqrt{a}}+11-5a[/tex]
Đặt [tex]t=\sqrt{a}[/tex]
[tex]f(a,b,c) \ge 2(t^3+\frac{1}{t^3}-\frac{5}{t})+11-5t^2=\frac{2t^6-5t^5+11t^3-10t^2+2}{t^3} \ge \frac{(t-1)^2(2t^4-t^3-4t^2+4t+2)}{t^3} \ge 0 [/tex]
Đáng ra anh phải chứng minh delta âm chứ ạ :-?? .
uhm đó cũng là 1 ý tưởng em thử làm coi xem thế nào

Bài này hok bik khó hok . mọi người thử nhé .
Cho [TEX]x,y,z >0[/TEX] và [TEX]x^3+y^3+z^3=1[/TEX]
C/m: [TEX]\frac{x^2}{\sqrt{1-x^2}}+\frac{y^2}{\sqrt{1-y^2}}+ \frac{z^2}{\sqrt{1-z^2}} \geq 2[/TEX]
đặt A= [TEX]\frac{x^2}{\sqrt{1-x^2}}+\frac{y^2}{\sqrt{1-y^2}}+ \frac{z^2}{\sqrt{1-z^2}} [/tex]Bài này hok bik khó hok . mọi người thử nhé .
Cho [TEX]x,y,z >0[/TEX] và [TEX]x^3+y^3+z^3=1[/TEX]
C/m: [TEX]\frac{x^2}{\sqrt{1-x^2}}+\frac{y^2}{\sqrt{1-y^2}}+ \frac{z^2}{\sqrt{1-z^2}} \geq 2[/TEX]

