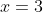Toán 10

[ngomaithuy93]

Bài 23: Cho hàm số:

1. Tìm m để h/s đạt CĐ, CT tại
   
   thỏa:
   
2. Cho
   
   có hoành độ
   
   và (D) là đường thẳng đi qua A và có hệ số góc bằng -2. Tìm m để (D) cắt (Cm) tại A, B, C sao cho A là trung điểm của BC.
3. Khi m=4, hãy khảo sát và vẽ đồ thị (C) của h/s và chứng tỏ rằng trên (C) không thể tồn tại 2 điểm sao cho 2 tiếp tuyến tại 2 điểm ấy vuông góc với nhau.
4. Hãy xác định a để trên (C) có 2 điểm P,Q sao cho:

1. [TEX]y'=3x^2-2mx+m+2[/TEX]
Đk để hs có CĐ, CT[TEX] \Leftrightarrow m^2-3(m+2)>0[/TEX]
Khi đó hđộ CĐ, CT là x1, x2
[TEX]Y/c \Leftrightarrow (x_1+x_2)^2-4x_1x_2<1 \Leftrightarrow \frac{4m^2}{9}-\frac{4(m+2)}{3}<1[/TEX]
Lấy giao 2 tập giá trị trên...
Cách làm là chủ yếu phải k?

2. A(3;-3m+32)
Đ/t d: y=-2x+38-3m
Hđộ gđ của d và (Cm) là nghiệm pt:
[TEX]x^3-mx^2+(m+4)x+4m-36=0[/TEX]
Thay tọa độ điểm uốn vào... :|

 

[hetientieu_nguoiyeucungban]

cho hàm số [TEX]y=\frac{x+1}{x-1}[/TEX](C)
nếu tam giác ABC nội tiếp (C) thì trực tâm H của tam giác ABC cũng thuộc (C)
làm giúp em vs

 

[acsimet_91]

Bài 23: Cho hàm số:

3.Khi m=4, hãy khảo sát và vẽ đồ thị (C) của h/s và chứng tỏ rằng trên (C) không thể tồn tại 2 điểm sao cho 2 tiếp tuyến tại 2 điểm ấy vuông góc với nhau.
4.Hãy xác định a để trên (C) có 2 điểm P,Q sao cho:

Chúc mọi người thi Tốt nghiệp thành công !

3; [TEX]y=f(x)=x^3-2x^2 + 4x -1[/TEX]

[TEX]f'(x)=3x^2 -4x + 4 \geq \frac{8}{3}[/TEX]

\Rightarrow [TEX] \forall x_1;x_2[/TEX] ta có: [TEX]f'(x_1).f'(x_2) \geq (\frac{8}{3})^2 >4[/TEX] ......(1)


Mặt khác: Qua điểm [TEX](x_1, f(x_1)); (x_2; f(x_2))[/TEX] kẻ được 2 tiếp tuyến vuông góc \Leftrightarrow [TEX]f'(x_1).f'(x_2) = -1[/TEX]..........(2)

[TEX](1) (2) \Rightarrow dpcm [/TEX]

4; Ý 3 vs ý 4 hình như ko độc lập?

[TEX]hpt \Leftrightarrow mx_P^2 - (m+2)x_P + 1-a = 0; mx_Q^2 -(m+2)x_Q + 1-a =0[/TEX]

\Rightarrow [TEX]x_P; x_Q[/TEX] là nghiệm của pt:

[TEX]mx^2 - (m+2)x +1-a=0[/TEX] (*)

Thay m=2 vào (*), tìm a để (*) có nghiệm.

 

[nguyendangkhoa11593]

cho hàm số [TEX]y=\frac{x+1}{x-1}[/TEX]
nếu tam giác ABC nội tiếp (C) thì trực tâm H của tam giác ABC cũng thuộc (C)
làm giúp em vs

đề bài này là như thế nào vậy bạn, (C) là đường gì, nếu (C) là đồ thị hàm số ở trên thì ABC nội tiếp (C) là như thế nào???:-SS

 

[ngomaithuy93]

Bài 25: Cho hs: [TEX]y=\frac{3x+1}{x-3} (C)[/TEX]
1. Tìm hs đối xứng với đồ thị hs trên qua đ/t x+y-3=0
2. M là điểm bất kì trên (C). Tiếp tuyến với (C) tại M cắt 2 TC của (C) tại A&B.
CMR: M là trung điểm của AB.

cho hàm số [TEX]y=\frac{x+1}{x-1}[/TEX](C)
nếu tam giác ABC nội tiếp (C) thì trực tâm H của tam giác ABC cũng thuộc (C)

Liệu có phải nội tiếp trg trường hợp này là tất cả các đỉnh của tam giác đều nằm trên đồ thị k nhỉ?

 

[silvery21]

Những bài đọc thấy lạ luôn nhé

bài 26: hàm số [TEX]\frac{2x+1}{x-2} [/TEX]. cmr đồ thị (C) có vô số cặp tiếp tuyến // ; đồng thời các đường thẳng nối tiếp điểm của các cặp tiếp tuyến này luôn đi qua 1 điểm cố định

bài 27: cho hs : [TEX]y = (x-2)^2.(2x-1)[/TEX] . tìm m để (C) có 2 tiếp tuyến cùng phương với đường thẳng y=mx . giả sử M; N là các cặp tiếp điểm cmr đường thẳng MN luôn đi qua 1 điểm cố định khi m biến thiên

Bài 28: cho [TEX]y = x^3 - 6x^2 +9x -4[/TEX] . x định k sao cho tồn tại 2 tiếp tuyến của đồ thị (C) có cùng hệ số góc k . 2 tiếp điểm M; N viết pt đường thẳng MN

Bài 29: cho hs [TEX]y=\frac{x-2}{x-1}[/TEX] . tìm các điểm trên Oy để từ đó kẻ được 2 tếp tuyến tới (C) sao cho 2 tiếp điểm tương ứng năm f về 2 phía đối với Ox

search thử google chỉ có câu 1 thoai . đúng là lạ thật )

 

[huutrang93]

cho hàm số [TEX]y=\frac{x+1}{x-1}[/TEX](C)
nếu tam giác ABC nội tiếp (C) thì trực tâm H của tam giác ABC cũng thuộc (C)
làm giúp em vs

Bài 25: Cho hs: [TEX]y=\frac{3x+1}{x-3} (C)[/TEX]
1. Tìm hs đối xứng với đồ thị hs trên qua đ/t x+y-3=0
2. M là điểm bất kì trên (C). Tiếp tuyến với (C) tại M cắt 2 TC của (C) tại A&B.
CMR: M là trung điểm của AB.


Liệu có phải nội tiếp trg trường hợp này là tất cả các đỉnh của tam giác đều nằm trên đồ thị k nhỉ?

Đúng rồi đó

Đổi về hệ IXY thì phương trình là [TEX]Y=2/X[/TEX]

Giả sử tọa độ [TEX]A(X_1;2/X_1), B(X_2,2/X_2), C(X_3,2/X_3), H(a;b)[/TEX]

[TEX]\vec{AB}=(X_2-X_1;2/X_2-2/X_1); \vec{AC}=(X_3-X_1;2/X_3-2/X_1)[/TEX]
[TEX]\vec{CH}=(a-X_3;b-2/X_3); \vec{BH}=(a-X_2,b-2/X_2)[/TEX]

Để H là trực tâm thì

[TEX]\vec{AB}.\vec{CH}=0 \Leftrightarrow (X_2-X_1)(a-X_3)+\frac{2(X_1-X_2)}{X_1X_2}(b-\frac{2}{X_3})=0 \Leftrightarrow a-X_3-\frac{1}{X_1X_2}(b-\frac{2}{X_3})=0 \Leftrightarrow X_1X_2X_3=aX_1X_2-b+2/X_3[/TEX]
[TEX]\vec{AC}.\vec{BH}=0 \Leftrightarrow (X_3-X_1)(a-X_2)+\frac{2(X_1-X_3)}{X_1X_3}(b-\frac{2}{X_2})=0 \Leftrightarrow a-X_2-\frac{1}{X_1X_3}(b-\frac{2}{X_2})=0 \Leftrightarrow X_1X_2X_3=aX_1X_3-b+2/X_2[/TEX]

Lấy 2 phương trình trừ nhau
[TEX]\Rightarrow a=\frac{2}{X_1X_2X_3}[/TEX]

Nhân X_3 vào phương trình trên, X_2 vào phương trình dưới rồi lấy 2 cái trừ nhau
[TEX]\Rightarrow b=X_1X_2X_3[/TEX]

Vậy H thuộc (C)



Bài 25:

a) Đổi về hệ IXY, phương trình (C): [TEX]Y=10/X,[/TEX] phương trình (d): [TEX]X+Y+3=0[/TEX]

Gọi [TEX]A(a;10/a)[/TEX] là điểm bất kì thuộc (C), [TEX]B(b;-3-b)[/TEX] là hình chiếu vuông góc của A xuống d, A' là điểm đối xứng với A qua B

Ta có
[TEX](-1)(b-a)+(-3-b-10/a)=0 \Rightarrow b=-1,5+0,5a-5/a[/TEX]

Do A' đối xứng với A qua B nên tọa độ A'
[TEX]X_{A'}=-3-10/a \Rightarrow -a=\frac{10}{X_{A'}+3}[/TEX]
[TEX]Y_{A'}=-3-a \Rightarrow -a=Y_{A'}+3[/TEX]

[TEX]\Rightarrow Y=\frac{10}{X_+3}-3 \Leftrightarrow y=\frac{10}{x}[/TEX]
là phương trình (C') đối xứng C qua d

b) đổi về hệ IXY, 2 tiệm cân là Y=0 và X=0

Gọi M là điểm bất kì trên (C) \Rightarrow [TEX]M(a;10/a)[/TEX]

Tiếp tuyến tại M
[TEX]Y=\frac{-10}{a^2}(X-a)+\frac{10}{a}=\frac{-10X}{a^2}+\frac{20}{a}[/TEX]

Tiếp tuyến này cắt 2 tiệm cân tại [TEX]C(0;20/a)[/TEX] và [TEX]D(2a;0)[/TEX]

Trung điểm CD là [TEX](a;10/a)[/TEX]

Vậy trung điểm CD là điểm M

 

[acsimet_91]

Những bài đọc thấy lạ luôn nhé

bài 26: hàm số [TEX]\frac{2x+1}{x-2} [/TEX]. cmr đồ thị (C) có vô số cặp tiếp tuyến // ; đồng thời các đường thẳng nối tiếp điểm của các cặp tiếp tuyến này luôn đi qua 1 điểm cố định

[TEX]y=f(x)=2+\frac{5}{x-2}[/TEX]

Đồ thị (C) có tiệm cận đứng [TEX]x=2;[/TEX]tiệm cận ngang [TEX]y=2[/TEX]

\Rightarrow [TEX]I(2;2)[/TEX] là điểm đối xứng của đồ thị.

[TEX]f'(x)=\frac{-5}{(x-2)^2}<0[/TEX]

Với [TEX] \forall a <0[/TEX] ta có:

[TEX]f'(x)=a \Leftrightarrow a(x-2)^2 + 5 =0 \Leftrightarrow ax^2-4ax+4a+5 =0[/TEX]....................(*)

NX: pt (*) có 2 nghiệm phân biệt với [TEX] \forall a <0 [/TEX]

\Rightarrow Đồ thị [TEX](C)[/TEX] có vô số tiếp tuyến song song.

Gọi [TEX]x_1; x_2[/TEX] là 2 nghiệm của (*)

[TEX]x_1+x_2=4[/TEX]


[TEX]f(x_1)+f(x_2)=4+\frac{5}{x_1-2} + \frac{5}{x_2-2}=4 + \frac{5(x_1+x_2)-20}{x_1-2)(x_2-2)}=4[/TEX]

\Rightarrow [TEX]M(x_1; f(x_1)); N(x_2; f(x_2))[/TEX] đối xứng nhau qua I

\Rightarrow [TEX]MN [/TEX] luôn đi qua [TEX]I(2,2)[/TEX] cố định.

\Rightarrow [TEX]dpcm[/TEX]

bài 27: cho hs : [TEX]y = (x-2)^2.(2x-1)[/TEX] . tìm m để (C) có 2 tiếp tuyến cùng phương với đường thẳng y=mx . giả sử M; N là các cặp tiếp điểm cmr đường thẳng MN luôn đi qua 1 điểm cố định khi m biến thiên

[TEX]y=f(x)=(x-2)^2.(2x-1)[/TEX]

[TEX]f'(x)=6.(x-1)(x-2)[/TEX]

[TEX]f''(x)= 6.(2x-3)[/TEX]

\Rightarrow [TEX](C)[/TEX] nhận [TEX]I(\frac{3}{2}; \frac{1}{2})[/TEX] làm điểm uốn.

[TEX](C)[/TEX] có 2 tiếp tuyến song song vs [TEX]y=mx[/TEX]

\Leftrightarrow [TEX]pt: f'(x)=m[/TEX] có 2 nghiệm phân biệt.

\Leftrightarrow [TEX]m>\frac{-3}{2}[/TEX]

Giả sử [TEX]M(x_1;f(x_1)); N(x_2; f(x_2))[/TEX] là tọa độ 2 tiếp điểm của 2 tiếp tuyến song song vs [TEX]y=mx[/TEX]

Chứng minh tương tự bài 26 \Rightarrow [TEX]M,N[/TEX] đối xứng nhau qua [TEX]I[/TEX]

\Rightarrow [TEX]MN[/TEX] luôn đi qua I cố định

 

[kenylklee]

Những bài đọc thấy lạ luôn nhé

bài 26: hàm số [TEX]\frac{2x+1}{x-2} [/TEX]. cmr đồ thị (C) có vô số cặp tiếp tuyến // ; đồng thời các đường thẳng nối tiếp điểm của các cặp tiếp tuyến này luôn đi qua 1 điểm cố định

bài 27: cho hs : [TEX]y = (x-2)^2.(2x-1)[/TEX] . tìm m để (C) có 2 tiếp tuyến cùng phương với đường thẳng y=mx . giả sử M; N là các cặp tiếp điểm cmr đường thẳng MN luôn đi qua 1 điểm cố định khi m biến thiên

Bài 28: cho [TEX]y = x^3 - 6x^2 +9x -4[/TEX] . x định k sao cho tồn tại 2 tiếp tuyến của đồ thị (C) có cùng hệ số góc k . 2 tiếp điểm M; N viết pt đường thẳng MN

Bài 29: cho hs [TEX]y=\frac{x-2}{x-1}[/TEX] . tìm các điểm trên Oy để từ đó kẻ được 2 tếp tuyến tới (C) sao cho 2 tiếp điểm tương ứng năm f về 2 phía đối với Ox

Uh, cũng mới và lạ đấy!

Bài 29: cho hs [TEX]y=\frac{x-2}{x-1}[/TEX] . tìm các điểm trên Oy để từ đó kẻ được 2 tếp tuyến tới (C) sao cho 2 tiếp điểm tương ứng năm f về 2 phía đối với Ox

Giải rồi!

bài 26: hàm số [TEX]\frac{2x+1}{x-2} [/TEX]. cmr đồ thị (C) có vô số cặp tiếp tuyến // ; đồng thời các đường thẳng nối tiếp điểm của các cặp tiếp tuyến này luôn đi qua 1 điểm cố định
Thử chém con này xem, chứ không biết có đúng hay sai! Mong mọi người cho ý kiến!

Xét pt

Ta có:

Vậy ứng với mỗi giá trị K<0 thì pt

có 2 nghiệm phân biệt

Điều này có nghĩa là ứng với một giá trị K<0 ta luôn tìm được trên (C) 2 điểm có hoành độ

sao cho tiếp tuyến tại các điểm ấy có hệ số góc là K.
Từ đó suy ra có vô số cặp điểm mà tiếp tuyến tại các tiếp điểm ấy song song với nhau ,

thỏa yêu cầu bài toán.
Ý 2: Theo tớ đến chổ này chúng ta sẽ tìm tung độ tiếp điểm từ hoành độ => viết pt đường thẳng có tham số K => khử K CM đường thẳng luôn qua điểm cố định, nghĩ vậy chứ chẳng biết đúng hok, làm biếng làm quá , hay làm giống Bác acsimet kia cho đỡ phải suy nghĩ

 

[silvery21]

[tex]y=f(x)=2+\frac{5}{x-2}[/tex]

đồ thị (c) có tiệm cận đứng [tex]x=2;[/tex]tiệm cận ngang [tex]y=2[/tex]

\rightarrow [tex]i(2;2)[/tex] là điểm đối xứng của đồ thị.

[tex]f'(x)=\frac{-5}{(x-2)^2}<0[/tex]

với [tex] \forall a <0[/tex] ta có:


[tex]f'(x)=a \leftrightarrow (x-2)^2 + 5a =0 \leftrightarrow x^2-4x+4+5a =0[/tex]....................(*) ..............cậu làm nhầm bước này . Qui đồng sai

..... ...

 

[silvery21]

Bài 10: Cho hs: [TEX]y=\frac{x+2}{x-1}(C)[/TEX]
Tìm trên trục tung điểm A: Từ A kẻ đc 2 tiếp tuyến đến (C) sao cho 2 tiếp điểm tg ứng nằm về 2 phía với trục hoành.

Phương pháp:
Gọi

là điểm bất kì mà đề bài yêu cầu tìm.
Xét đường thẳng

bất kì qua A và có hệ số góc là K thì:

tiếp xúc với (C) <=> Hệ pt sau có nghiệm:

........

Ý tiếp theo là 2 tiếp điểm nằm về 2 phía của trục hoành, tức là tung độ của 2 tiếp điểm này nhân lại là âm.

!

c có chắc bước đó chỉ cần điều kiện đêy' ko c

theo t mình còn phải để ý cái tiệm cận đứng nữa chứ c

 

[acsimet_91]

Bài 28: cho [TEX]y = x^3 - 6x^2 +9x -4[/TEX] . x định k sao cho tồn tại 2 tiếp tuyến của đồ thị (C) có cùng hệ số góc k . 2 tiếp điểm M; N viết pt đường thẳng MN

Bài 29: cho hs [TEX]y=\frac{x-2}{x-1}[/TEX] . tìm các điểm trên Oy để từ đó kẻ được 2 tếp tuyến tới (C) sao cho 2 tiếp điểm tương ứng năm f về 2 phía đối với Ox

Ừ, quy đồng sai thật. Ngại quá . sửa rồi

Bài 29:

[TEX]y=f(x)=1-\frac{1}{x-1}[/TEX]

[TEX]f'(x)=\frac{1}{(x-1)^2}[/TEX]

Giả sử [TEX]M(0,m)[/TEX]

Phương trình đường thẳng qua M có hệ số góc k có dạng:

[TEX](d): y=kx+m[/TEX]

Qua M kẻ đươc 2 tiếp tuyến tới (C) sao cho 2 tiếp điểm tương ứng nằm về 2 phía đối với [TEX]Ox[/TEX]

\Leftrightarrow hệ sau có nghiệm [TEX](k_1;x_1); (k_2;x_2)[/TEX]thỏa mãn [TEX]f(x_1).f(x_2)<0:[/TEX]

[TEX]\frac{1}{(x-1)^2}=k[/TEX]...................................(1)

[TEX]1-\frac{1}{x-1}=kx+m[/TEX]......................................(2)

Thay (1) vào (2) được hệ:

[TEX]\frac{1}{(x-1)^2}=k[/TEX].....................................(3)

[TEX](m-1)(x-1)^2+2.(x-1) +1 =0[/TEX]...........................(4)

[TEX]x \not= 1[/TEX]

Hệ trên có 2 nghiệm phân biệt

\Leftrightarrow [TEX]pt (4)[/TEX] có 2 nghiệm phân biệt khác 1

\Leftrightarrow [TEX]m<2;m \not=1[/TEX]............................................(5)

Mặt khác ta có:

[TEX]x_1 + x_2= \frac{-2}{m-1}[/TEX]

[TEX]x_1.x_2=\frac{1}{m-1}[/TEX]

[TEX]f(x_1).f(x_2) < 0 \Leftrightarrow(1-\frac{1}{x_1-1}).(1-\frac{1}{x_2-1}) <0[/TEX]

\Leftrightarrow [TEX]1-\frac{x_1+x_2-3}{x_1x_2-(x_1+x_2)+1} <0[/TEX]

thay vào,giải [TEX]bpt [/TEX] trên, kết hợp vs (5) tìm được tập giá trị của [TEX]m[/TEX]

Bài 28 hình như cũng có vô số cặp tiếp tuyến hả? Vậy MN thay đổi. Viết pt MN theo tham số hả?

Làm nhảm nãy giờ, ko biết đúng ko nữa

 

[kenylklee]

c có chắc bước đó chỉ cần điều kiện đêy' ko c

theo t mình còn phải để ý cái tiệm cận đứng nữa chứ c

Uhm, chắc là phải có thêm điều kiện hoành độ tiếp điểm khác tiệm cận đứng nữa, mình cũng không biết chắc. Tại mình không được đào tạo bài bản, toàn là tự chế cách làm không . bài 28 đọc đi đọc lại mà chẳng hiểu cái đề muốn gì, thâm thúy thiệt, vừa mang tính chất cố định lại mang tính chất "vô định" (tạm gọi là vậy) )

 

[silvery21]

Uhm, chắc là phải có thêm điều kiện hoành độ tiếp điểm khác tiệm cận đứng nữa, mình cũng không biết chắc. Tại mình không được đào tạo bài bản, toàn là tự chế cách làm không . bài 28 đọc đi đọc lại mà chẳng hiểu cái đề muốn gì, thâm thúy thiệt, vừa mang tính chất cố định lại mang tính chất "vô định" (tạm gọi là vậy) )

uk . thì t cũng vậy thôi làm mấy đề thi thử thì phần này dễ lắm . nhưng xem trang này của các bạn có 1 số bài hay nên t tìm hiểu thì gặp mấy câu đó

acsimet_91: bài 29 t vẫn thấy thiếu cái j đó vì vẽ hình ra đk như vậy là chưa đủ
2 cái nhánh của đồ thị cần có đk với tiệm cận đứng nữa đó ..t ko bjk xử lý nữa thế nào . thôi kệ vậy lcus # rảnh thì tìm hiểu

 

[kenylklee]

Chúng ta cố gắng từ giờ đến lúc thi là sẽ nắm bắt phần lớn các dạng Toán khảo sát nha các bạn! Cố lên nào! Phát động cuộc chiến mới thôi! >-:-SS

Bài 30: Cho (Cm):

Định m để (Cm) có trục đối xứng vuông góc với trục hoành.

Dạng bài tập liên quan đến điểm uốn!
Bài 31: Cho hàm số

(C). Chứng minh rằng:

1. Khi a>0 thì tiếp tuyến tại điểm uốn của (C) có hệ số góc nhỏ nhất.
2. Khi a<0 thì tiếp tuyến tại điểm uốn của (C) có hệ số góc lớn nhất.

Bài 32: Cho đồ thị (C):

. Tìm các điểm trên đồ thị (C) sao cho từ đó kẻ được duy nhất 1 tiếp tuyến với đồ thị.

 

[atulara]

Bài 33:

Cho hàm số: [TEX]y = 2{x}^{3} + (m + 1){x}^{2} -2(m + 4)x +1[/TEX] [TEX]({C}_{m})[/TEX]
Với giá trị nào của m thì [TEX]({C}_{m})[/TEX] đạt cực đại, cực tiểu tại [TEX]{x}_{1}[/TEX], [TEX]{x}_{2}[/TEX] sao cho : [TEX]{{x}_{1}}^{2} + {{x}_{2}}^{2} \leq 2[/TEX]

 

[kenylklee]

Bài 33:

Cho hàm số: [TEX]y = 2{x}^{3} + (m + 1){x}^{2} -2(m + 4)x +1[/TEX] [TEX]({C}_{m})[/TEX]
Với giá trị nào của m thì [TEX]({C}_{m})[/TEX] đạt cực đại, cực tiểu tại [TEX]{x}_{1}[/TEX], [TEX]{x}_{2}[/TEX] sao cho : [TEX]{{x}_{1}}^{2} + {{x}_{2}}^{2} \leq 2[/TEX]

Tính y'
Sau đó tìm điều kiện để y'=0 có 2 nghiệm phân biệt
tức là Delta >0 và a#0
Ý 2:

Áp dụng Viet đối với y' ===> tìm được m

 

[qhoang1993]

Bài 34 Xác định (Cm):y=x^3-(m+3)x^2+3mx-2m có cực trị có hoành độ thỏ 1/x_1^2 + 1/x_2^2=4/9

 

[qhoang1993]

y = (x-2)/x (C)
Tìm trên (C) những điểm M sao cho tổng các khoảng cách từ M đến các trục tọa độ là nhỏ nhất

 

[ngomaithuy93]

Bài 30: Cho (Cm):

Định m để (Cm) có trục đối xứng vuông góc với trục hoành.

Giả sử (Cm) có trục đối xứng là x=t (do trục đối xứng vg góc với trục hoành).
Khi đó: Nếu điểm có hoành độ (t-x) thuộc đồ thị thì điểm có hđộ (t+x) cũng thuộc đồ thị. Ta có:
[TEX] (t-x)^4+(m+3)(t-x)^3+2(m+1)(t-x)^2=(t+x)^4+(m+3)(t+x)^3+2(m+1)(t+x)^2[/TEX]
[TEX]\Leftrightarrow x^2(2m+6-8t)+6mt^2+18t^2+8mt+8t-8t^3=0[/TEX]
pt này phải đúng với mọi x
[TEX]\Leftrightarrow \left{{m=4t-3}\\{6mt^2+18t^2+8mt+8t-8t^3=0} \Leftrightarrow t=...[/TEX]

Bài 31: Cho hàm số

(C). Chứng minh rằng:

1. Khi a>0 thì tiếp tuyến tại điểm uốn của (C) có hệ số góc nhỏ nhất.
2. Khi a<0 thì tiếp tuyến tại điểm uốn của (C) có hệ số góc lớn nhất.

Hoành độ điểm uốn là nghiệm pt y''=0 nên cũng là các điểm CĐ, CT của hs f(x)=y'.
Ứng với các giá trị a mang dấu âm/dương, lập BBT \Rightarrow đpcm.