L
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
- Status
- Không mở trả lời sau này.
T
thuylinha1k7
mình làm được rùi. chỉ cần tìm tọa độ 3 đỉnh A,B,C theo tham số.
sau đó gọi ph dg cao kẻ từ A là d1 ta có ud1.vecto BC=0
và tương tụ ta có 1 pt nữa đối với cạnh AC
giải hệ ph 2 ẩn số là ra đáp án
sau đó gọi ph dg cao kẻ từ A là d1 ta có ud1.vecto BC=0
và tương tụ ta có 1 pt nữa đối với cạnh AC
giải hệ ph 2 ẩn số là ra đáp án
P
pigletu
mình làm được rùi. chỉ cần tìm tọa độ 3 đỉnh A,B,C theo tham số.
sau đó gọi ph dg cao kẻ từ A là d1 ta có ud1.vecto BC=0
và tương tụ ta có 1 pt nữa đối với cạnh AC
giải hệ ph 2 ẩn số là ra đáp án
làm thế dễ nhầm lắm
lúc đầu phải đặt 2 tham số
------------------------------
D
dinh_nguyenvan91
P
pigletu
Bài 2: Cho parabol (P) [tex] y^2=2px[/tex] (p>0), A là một điểm cố định trên (P). Một góc vuông đỉnh A có các cạnh cắt (P) tại hai điểm B, C. CMR đường thẳng BC luôn đi qua một điểm cố định
A(x, y) thuộc (P)
B(
\Rightarrow pt AB
AB vuông góc AC \Rightarrow pt AC
tđ C là nghiệm của hệ
\Rightarrow pt BC
gs BC luôn đi qua I (
\Rightarrow đpcm
p/s cách này dài, lằng nhằng dễ nhầm nhưng t chẳng nghĩ ra cách nào khá nữa cả
N
nerversaynever
Đặt [TEX]A\left( {\frac{{y_0^2 }}{{2p}};y_0 } \right),B\left( {\frac{{y_1^2 }}{{2p}};y_1 } \right);C\left( {\frac{{y_2^2 }}{{2p}};y_2 } \right),y_o \ne y_1 \ne y_2 [/TEX]
AB,AC lần lượt có các vecto chỉ phương
[TEX]\begin{array}{l}u_1 \left( {y_1 + y_0 ;2p} \right);u_2 \left( {y_2 + y_0 ;2p} \right) \\ AB \bot AC \Leftrightarrow \left( {y_1 + y_0 } \right)\left( {y_2 + y_0 } \right) + 4p^2 = 0 \\ \end{array}[/TEX]
[TEX]\Leftrightarrow y_1 y_2 = - 4p^2 - y_0 \left( {y_1 + y_2 } \right) - y_0^2 [/TEX]
pt đường thẳng BC
[TEX]\begin{array}{l} BC:2p\left( {x - \frac{{y_1^2 }}{{2p}}} \right) - \left( {y_1 + y_2 } \right)\left( {y - y_1 } \right) = 0 \\ \Leftrightarrow 2px - \left( {y_1 + y_2 } \right)y + y_1 y_2 = 0 \\ 2px - \left( {y_1 + y_2 } \right)\left( {y + y_0 } \right) - 4p^2 - y_0^2 = 0 \\ \end{array}[/TEX]
g/s BC đi qua điểm cố định khi đó tồn tại x,y sao cho pt
[TEX]2px - \left( {y_1 + y_2 } \right)\left( {y + y_0 } \right) - 4p^2 - y_0^2 = 0[/TEX] với mọi y1;y2
điều đó tương đương
[TEX]\left\{ \begin{array}{l} y = - y_0 \\ x = 2p + \frac{{y_0^2 }}{{2p}} \\\end{array} \right.[/TEX]
AB,AC lần lượt có các vecto chỉ phương
[TEX]\begin{array}{l}u_1 \left( {y_1 + y_0 ;2p} \right);u_2 \left( {y_2 + y_0 ;2p} \right) \\ AB \bot AC \Leftrightarrow \left( {y_1 + y_0 } \right)\left( {y_2 + y_0 } \right) + 4p^2 = 0 \\ \end{array}[/TEX]
[TEX]\Leftrightarrow y_1 y_2 = - 4p^2 - y_0 \left( {y_1 + y_2 } \right) - y_0^2 [/TEX]
pt đường thẳng BC
[TEX]\begin{array}{l} BC:2p\left( {x - \frac{{y_1^2 }}{{2p}}} \right) - \left( {y_1 + y_2 } \right)\left( {y - y_1 } \right) = 0 \\ \Leftrightarrow 2px - \left( {y_1 + y_2 } \right)y + y_1 y_2 = 0 \\ 2px - \left( {y_1 + y_2 } \right)\left( {y + y_0 } \right) - 4p^2 - y_0^2 = 0 \\ \end{array}[/TEX]
g/s BC đi qua điểm cố định khi đó tồn tại x,y sao cho pt
[TEX]2px - \left( {y_1 + y_2 } \right)\left( {y + y_0 } \right) - 4p^2 - y_0^2 = 0[/TEX] với mọi y1;y2
điều đó tương đương
[TEX]\left\{ \begin{array}{l} y = - y_0 \\ x = 2p + \frac{{y_0^2 }}{{2p}} \\\end{array} \right.[/TEX]
Last edited by a moderator:
M
micoo
[toán 10]tìm tọa độ các điểm
trong mp Oxy cho 3 đường thẳng d1:3x-y-4=0
d2:x+y-6=0
d3:x-3=0
A,C thuộc d3,B thuộc d1,D thuộc d2.Tìm tọa độ các đỉnh của hình vuông ABCD
trong mp Oxy cho 3 đường thẳng d1:3x-y-4=0
d2:x+y-6=0
d3:x-3=0
A,C thuộc d3,B thuộc d1,D thuộc d2.Tìm tọa độ các đỉnh của hình vuông ABCD
Last edited by a moderator:
B
boykute_dk
[toán 10]toán tọa độ!!!
Câu 1: Trong mp Oxy cho A(2;1). Lấy điểm B thuộc trục Ox và hoành độ không âm, lấy điểm C thuộc trục Oy có tung độ không âm sao cho tam giác ABC vuông tại A. Tìm B,C sao cho tam giác ABC có diện tích lớn nhất.
Câu 2: Trong mp Oxy cho điểm M(1;2), 1 đường thẳng (d) qua M cắt 2 trục tọa độ Ox, Oy lần lượt tại A(a;0) và B(0;b) với a,b >0. Tìm pt (d) biết tam giác OAB có diện tích lớn nhất.
Giải dùm mềnh nhak, thnks nhìu !!
!!
Câu 1: Trong mp Oxy cho A(2;1). Lấy điểm B thuộc trục Ox và hoành độ không âm, lấy điểm C thuộc trục Oy có tung độ không âm sao cho tam giác ABC vuông tại A. Tìm B,C sao cho tam giác ABC có diện tích lớn nhất.
Câu 2: Trong mp Oxy cho điểm M(1;2), 1 đường thẳng (d) qua M cắt 2 trục tọa độ Ox, Oy lần lượt tại A(a;0) và B(0;b) với a,b >0. Tìm pt (d) biết tam giác OAB có diện tích lớn nhất.
Giải dùm mềnh nhak, thnks nhìu
B
boykute_dk
A
anhsao3200
Câu 1: Trong mp Oxy cho A(2;1). Lấy điểm B thuộc trục Ox và hoành độ không âm, lấy điểm C thuộc trục Oy có tung độ không âm sao cho tam giác ABC vuông tại A. Tìm B,C sao cho tam giác ABC có diện tích lớn nhất.
Câu 2: Trong mp Oxy cho điểm M(1;2), 1 đường thẳng (d) qua M cắt 2 trục tọa độ Ox, Oy lần lượt tại A(a;0) và B(0;b) với a,b >0. Tìm pt (d) biết tam giác OAB có diện tích lớn nhất.
Giải dùm mềnh nhak, thnks nhìu!!
Câu 2 : Theo mình nghĩ là tìm min thôi chứ tìm max có vẻ như ko xác định được mình sẽ giải theo tìm min bạn nhé
(d) đi qua A(a;0) B(0;b) có dạng
M(1,2) thuộc (d)
A
anhsao3200
Ta cóCâu 1: Trong mp Oxy cho A(2;1). Lấy điểm B thuộc trục Ox và hoành độ không âm, lấy điểm C thuộc trục Oy có tung độ không âm sao cho tam giác ABC vuông tại A. Tìm B,C sao cho tam giác ABC có diện tích lớn nhất.
A(2,1),B(x,0),C(0,c) dẫn đến
Từ đề bài Ta có hệ
Giải hệ tìm nghiệm rồi thay vào xem S của ABC lớn nhất bạn nhé
L
linda_hm
bài này thì mình chỉ hướng dẫn cách giải thôi nhé
trước tiên bạn phải tìm toạ độ giao điểm I (chứa ẩn) của AC và BD.vẽ hình ra ta sẽ xác định được ngay=>ta sẽ viết được pt đường thẳng BD(đi qua I và vuông góc với AC) sau đó tìm được toạ độ điểm B bằng cách xét 2 điểm B,D đối xứng qua I(B,D thuộc pt đường thẳng BD)..............
trước tiên bạn phải tìm toạ độ giao điểm I (chứa ẩn) của AC và BD.vẽ hình ra ta sẽ xác định được ngay=>ta sẽ viết được pt đường thẳng BD(đi qua I và vuông góc với AC) sau đó tìm được toạ độ điểm B bằng cách xét 2 điểm B,D đối xứng qua I(B,D thuộc pt đường thẳng BD)..............
B
boykute_dk
Ta có
A(2,1),B(x,0),C(0,c) dẫn đến
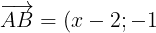;\overrightarrow{AC}=(-2;y-1))
Từ đề bài Ta có hệ

Giải hệ tìm nghiệm rồi thay vào xem S của ABC lớn nhất bạn nhé
Cho mình hỏi S tam giác ABC lớn nhất khi nào vậy???
T
tumonobeo
từ đề bài ta chỉ có :vecto AB . vecto AC = 0 chứ ko có AB^2 = AC ^2 đâu
từ vecto AB. Vecto AC =0 ta sẽ đc y=5-2x
vậy S max <=> AB . AC =[TEX]\sqrt{({(x-2)}^{2}+1)*(4+{(y-1)}^{2})}[/TEX] max
thay y=5-2x vào để đc pt bậc 2 nghiệm x
x^2 -4x+5=(x-2)^2 +1 -> min <=>x= 2
từ vecto AB. Vecto AC =0 ta sẽ đc y=5-2x
vậy S max <=> AB . AC =[TEX]\sqrt{({(x-2)}^{2}+1)*(4+{(y-1)}^{2})}[/TEX] max
thay y=5-2x vào để đc pt bậc 2 nghiệm x
x^2 -4x+5=(x-2)^2 +1 -> min <=>x= 2
A
anhsao3200
xin lỗi mình nhầm đề ..............................................................nhưng cậu viết mình ko hiểu chỗ S max rồi suy ra pt rồi suy ra min rồi suy ra x=2 là sao bạn giải thích rõ được kotừ đề bài ta chỉ có :vecto AB . vecto AC = 0 chứ ko có AB^2 = AC ^2 đâu
từ vecto AB. Vecto AC =0 ta sẽ đc y=5-2x
vậy S max <=> AB . AC =[TEX]\sqrt{({(x-2)}^{2}+1)*(4+{(y-1)}^{2})}[/TEX] max
thay y=5-2x vào để đc pt bậc 2 nghiệm x
x^2 -4x+5=(x-2)^2 +1 -> min <=>x= 2
T
tumonobeo
M
minhthanhtrancp
mình cũng đóng góp 1 bài khá hay ^^!
Cho hình vuông ABCD biết M(2,1) , N(4; -2) , P(2;0), Q(1;2) lần lượt thuộc cạnh AB, BC, CD, AD. hÃy lập phương trình các cạnh của hình vuông ABCD.
Cho hình vuông ABCD biết M(2,1) , N(4; -2) , P(2;0), Q(1;2) lần lượt thuộc cạnh AB, BC, CD, AD. hÃy lập phương trình các cạnh của hình vuông ABCD.
D
duynhan1
Gọi [TEX]\vec{n} = (a;b)\ (a^2 +b^2 \not=0)[/TEX] là vecto pháp tuyến của đường thẳng AB [TEX]\Rightarrow \vec{m}=(b;-a)[/TEX] là vecto pháp tuyến của đường thẳng BC.mình cũng đóng góp 1 bài khá hay ^^!
Cho hình vuông ABCD biết M(2,1) , N(4; -2) , P(2;0), Q(1;2) lần lượt thuộc cạnh AB, BC, CD, AD. hÃy lập phương trình các cạnh của hình vuông ABCD.
Ta có :
[TEX]\left{ AB:\ a(x-2)+b(y-1)= 0 \\ BC:\ b(x-4) - a(y+2) = 0 [/TEX]
ABCD là hình vuông khi và chỉ khi :
[TEX]d(P;AB) = d(Q;BC)[/TEX]
Còn lại các bạn tự giải nhé
B
boykute_dk
B
boykute_dk
từ đề bài ta chỉ có :vecto AB . vecto AC = 0 chứ ko có AB^2 = AC ^2 đâu
từ vecto AB. Vecto AC =0 ta sẽ đc y=5-2x
vậy S max <=> AB . AC =[TEX]\sqrt{({(x-2)}^{2}+1)*(4+{(y-1)}^{2})}[/TEX] max
thay y=5-2x vào để đc pt bậc 2 nghiệm x
x^2 -4x+5=(x-2)^2 +1 -> min <=>x= 2
Bạn có thể giải rõ hơn ko, mình thấy nếu thay y vào rồi khai triển thì ra pt bậc 4 luôn =.+!
- Status
- Không mở trả lời sau này.

