N
- Status
S
satthiendk1
Bài tập khó đay. Cứu em với.thank
cho tam giác ABC : 3vectoMA + 4vectoMB= vecto0
vectoCN=1/2vectoBC
G là trọng tâm tam giác ABC
a/ cm: M<G<N thẳng hàng
b/ tính AC THEO AG và An .Ac \bigcap_{}^{}Gn=P
tính tỉ số PA/PC
2/cho hbhABCD : AI=aAB; ẠI=bBC
cm I<J<K thẳng hàng
.1/b=1/a+1/c
nhanh nha
cho tam giác ABC : 3vectoMA + 4vectoMB= vecto0
vectoCN=1/2vectoBC
G là trọng tâm tam giác ABC
a/ cm: M<G<N thẳng hàng
b/ tính AC THEO AG và An .Ac \bigcap_{}^{}Gn=P
tính tỉ số PA/PC
2/cho hbhABCD : AI=aAB; ẠI=bBC
cm I<J<K thẳng hàng
.1/b=1/a+1/c
nhanh nha
N
noinhobinhyen
C
cudiat97
toán về hệ thức lượng lớp 10
1)cho AB =K.Tìm tập hợp M thoả MA^2 +MB^2=5K^2/2
2)S=1/4(a+b-c)(a+c-b).Tam giác ABC là tam giac gì?
3)a=b.cosC+c.cosB
4)sinB.cosC+sinC.cosB=sinA
1)cho AB =K.Tìm tập hợp M thoả MA^2 +MB^2=5K^2/2
2)S=1/4(a+b-c)(a+c-b).Tam giác ABC là tam giac gì?
3)a=b.cosC+c.cosB
4)sinB.cosC+sinC.cosB=sinA
L
likecream
L
lovelybones311
Gợi ý :
3)$b.cosC+c.cosB=b.\dfrac{a^2+b^2-c^2}{2ab}+ c.\dfrac{a^2+c^2-b^2}{2ac}$
4)$sin B =\dfrac{b}{2R}.\dfrac{a^2+b^2-c^2}{2ab}+ \dfrac{c}{2R}.\dfrac{a^2+c^2-b^2}=\dfrac{a}{2R}=sin A$
1) Gọi O là trung điểm AB ...ta có
$MO^2=\dfrac{MA^2+ MB^2}{2} -\dfrac{AB^2}{4} =\dfrac{5k^2-k^2}{4}=k^2$
=>$MO =k $(AB =k >0)
k ko đổi => M thuộc đường tròn (O;k)
2)S=1/4(a+b-c)(a+c-b).Tam giác ABC là tam giac gì?
Gợi ý :Sử dụng công thức Hê-rông
Ta có :
$S=\dfrac{1}{4}.(a+b-c)(a+c-b)=\dfrac{a+b+c-2c}{2}.\dfrac{a+b+c-2b}{2}=(p-b).(p-c)$
Đặt $p=\dfrac{a+b+c}{2}$
Mà [tex]S=\sqrt{p.(p-a).(p-b).(p-c)[/tex]
=>[tex]\sqrt{(p-b).(p-c)}=\sqrt{p.(p-a)}[/tex]
=>$(p-b).(p-c)=p.(p-a)$
Phá tung cái biểu thức cuối ra sẽ được
$a^2=b^2+c^2$
=> tam giác ABC vuông tại A
Last edited by a moderator:
1
123456784
[toán 10] tìm giá trị nhỏ nhất
1) $y=\frac{x}{2}+\frac{8}{x} $ với $x>0$
2) $y= 2x+\frac{1}{x^2}$ với $x>0$
3)$y=2x^3+\frac{3}{x^2}$ với $x>0$
Thầy mình nói là áp dụng bất đẳng thức Cô-si
1) $y=\frac{x}{2}+\frac{8}{x} $ với $x>0$
2) $y= 2x+\frac{1}{x^2}$ với $x>0$
3)$y=2x^3+\frac{3}{x^2}$ với $x>0$
Thầy mình nói là áp dụng bất đẳng thức Cô-si
A
anh_doan_ttg
Giải hộ mấy bài làm mẫu
Xét tính đơn điệu của hàm số:
a, $y=2x+5$
b, $y=x^2-2x +4$
c,$y=\frac{x+1}{x-1}$
gợi ý cách làm cho em theo dạng nha
Xét tính đơn điệu của hàm số:
a, $y=2x+5$
b, $y=x^2-2x +4$
c,$y=\frac{x+1}{x-1}$
gợi ý cách làm cho em theo dạng nha
Last edited by a moderator:
N
nguyenbahiep1
H
huytrandinh
[TEX]1/\frac{x}{2}+\frac{8}{x}\geq 2 \sqrt{\frac{x}{2}.\frac{8}{x}}=4[/TEX]
[TEX]min=4<=>x=4[/TEX]
[TEX]2/ 2x+\frac{1}{x^{2}}=x+x+\frac{1}{x^{2}}[/TEX]
[TEX]\geq 3 \sqrt[3]{x.x.\frac{1}{x^{2}}}=3[/TEX]
[TEX]<=>min=3<=>x=1[/TEX]
[TEX]3/ 2x^{3}+\frac{3}{x^{2}}[/TEX]
[TEX]=x^{3}+x^{3}+\frac{1}{x^{2}}+\frac{1}{x^{2}}+\frac{1}{x^{2}}[/TEX]
[TEX]\geq 5\sqrt[5]{x^{3}.x^{3}.\frac{1}{x^{2}.x^{2}.x^{2}}}=5[/TEX]
[TEX]=>min=5<=>x=1[/TEX]
[TEX]min=4<=>x=4[/TEX]
[TEX]2/ 2x+\frac{1}{x^{2}}=x+x+\frac{1}{x^{2}}[/TEX]
[TEX]\geq 3 \sqrt[3]{x.x.\frac{1}{x^{2}}}=3[/TEX]
[TEX]<=>min=3<=>x=1[/TEX]
[TEX]3/ 2x^{3}+\frac{3}{x^{2}}[/TEX]
[TEX]=x^{3}+x^{3}+\frac{1}{x^{2}}+\frac{1}{x^{2}}+\frac{1}{x^{2}}[/TEX]
[TEX]\geq 5\sqrt[5]{x^{3}.x^{3}.\frac{1}{x^{2}.x^{2}.x^{2}}}=5[/TEX]
[TEX]=>min=5<=>x=1[/TEX]
A
anh_doan_ttg
Hình 10 vector
Cho tam giác ABC và điểm M t/m:
$\vec{BM}=\vec{BC}-2\vec{AB}$
N là điểm t/m
$\vec{CN}=x\vec{AC}-\vec{BC};x \in R$
a, Tìm $x$ để $A,M,N$ thẳng hàng
b, Tìm $x$ để $MN$ qua trung điểm I của BC.Tính $\dfrac{IM}{IN}$
Cho tam giác ABC và điểm M t/m:
$\vec{BM}=\vec{BC}-2\vec{AB}$
N là điểm t/m
$\vec{CN}=x\vec{AC}-\vec{BC};x \in R$
a, Tìm $x$ để $A,M,N$ thẳng hàng
b, Tìm $x$ để $MN$ qua trung điểm I của BC.Tính $\dfrac{IM}{IN}$
Last edited by a moderator:
N
noinhobinhyen
Ta có :
a.$\vec{CN}=x\vec{AC}-\vec{BC}$
$\Rightarrow \vec{CN}+\vec{BC}=x\vec{AC}$
$\Rightarrow \vec{BN}=x\vec{AC}$
$\Rightarrow BN // AC$
Có
$\vec{BM}=\vec{BC}-2\vec{AB}$
$\Leftrightarrow \vec{BM}+\vec{AB}=\vec{BC}-\vec{AB}$
$\Leftrightarrow \vec{AM}=2\vec{BK}$
Với $K$ là trung điểm $AC$
$\Rightarrow AM //BK$
$A;M;N$ thẳng hàng $\Leftrightarrow AN // BK ; BN // AK$
$\Rightarrow AKBN$ là hình bình hành
$\Rightarrow BN=AK=\dfrac{1}{2}AC$
$\Rightarrow x=\dfrac{-1}{2}$
b.Gọi I là trung điểm BC
$\vec{IM}=2\vec{IA}+3\vec{IC}$
$\vec{IN}=-x\vec{IA}+(x-1)\vec{IC}$
$\vec{IM} ; \vec{IN}$ cùng phương $\Leftrightarrow x=\dfrac{2}{5}$
a.$\vec{CN}=x\vec{AC}-\vec{BC}$
$\Rightarrow \vec{CN}+\vec{BC}=x\vec{AC}$
$\Rightarrow \vec{BN}=x\vec{AC}$
$\Rightarrow BN // AC$
Có
$\vec{BM}=\vec{BC}-2\vec{AB}$
$\Leftrightarrow \vec{BM}+\vec{AB}=\vec{BC}-\vec{AB}$
$\Leftrightarrow \vec{AM}=2\vec{BK}$
Với $K$ là trung điểm $AC$
$\Rightarrow AM //BK$
$A;M;N$ thẳng hàng $\Leftrightarrow AN // BK ; BN // AK$
$\Rightarrow AKBN$ là hình bình hành
$\Rightarrow BN=AK=\dfrac{1}{2}AC$
$\Rightarrow x=\dfrac{-1}{2}$
b.Gọi I là trung điểm BC
$\vec{IM}=2\vec{IA}+3\vec{IC}$
$\vec{IN}=-x\vec{IA}+(x-1)\vec{IC}$
$\vec{IM} ; \vec{IN}$ cùng phương $\Leftrightarrow x=\dfrac{2}{5}$
1
123456784
[toán 10] co-si và bunhiacopxkia
Chứng minh rằng:
1) Với mọi số dương a,b,c. Ta luôn có:
$(a+b)(b+c)(c+a) >= 8abc$
2) Cho a,b,c là độ dài ba cạnh tam giác:
CMR: $ab(a+b-2c)+bc(b+c-2a)+ca(c+a-2b) >=0$
3) Cho $a+b+c+d=2$
CMR: $a^2+b^2+c^2+d^2=1$
Chứng minh rằng:
1) Với mọi số dương a,b,c. Ta luôn có:
$(a+b)(b+c)(c+a) >= 8abc$
2) Cho a,b,c là độ dài ba cạnh tam giác:
CMR: $ab(a+b-2c)+bc(b+c-2a)+ca(c+a-2b) >=0$
3) Cho $a+b+c+d=2$
CMR: $a^2+b^2+c^2+d^2=1$
H
hoangtrongminhduc
1
[TEX]a+b\geq2\sqrt{ab}[/TEX]
[TEX]a+c\geq2\sqrt{ac}[/TEX]
[TEX]b+c\geq2\sqrt{bc}[/TEX]
nhân vế theo vế ta đc
[TEX](a+b)(a+c)(b+c)\geq8\sqrt{abacbc}[/TEX]
<=>[TEX](a+b)(a+c)(b+c)\geq8abc[/TEX]
[TEX]a+b\geq2\sqrt{ab}[/TEX]
[TEX]a+c\geq2\sqrt{ac}[/TEX]
[TEX]b+c\geq2\sqrt{bc}[/TEX]
nhân vế theo vế ta đc
[TEX](a+b)(a+c)(b+c)\geq8\sqrt{abacbc}[/TEX]
<=>[TEX](a+b)(a+c)(b+c)\geq8abc[/TEX]
H
huytrandinh
câu 2
[TEX]<=>ab(a+b)+bc(b+c)+ac(a+c)\geq 6abc[/TEX]
[TEX]<=>(a^{2}b+b^{2}c)+(ab^{2}+ac^{2})+(bc^{2}+a^{2}c)\geq 6abc[/TEX]
cauchy từung biểu thức trong ngoặc cộng lại ta có đpcm
[TEX]<=>ab(a+b)+bc(b+c)+ac(a+c)\geq 6abc[/TEX]
[TEX]<=>(a^{2}b+b^{2}c)+(ab^{2}+ac^{2})+(bc^{2}+a^{2}c)\geq 6abc[/TEX]
cauchy từung biểu thức trong ngoặc cộng lại ta có đpcm
D
doanthienhuong
các bạn ơi, cho mình hỏi câu C bài này 1 tý
cho A(1,2) B(1,-3) C(-2,1)
a/ cm A,B,C là 3 đỉnh 1 tam giác
b/ tìm tọa độ trực tâm H,tâm I tâm đường tròn ngoại tiếp và tâm J tâm đường tròn nội tiếp tam giác ABC
c/ TÌM TỌA ĐỘ ĐIỂM M SAO cho
MA+MB min
MB+MC min
MA-MC max
cho A(1,2) B(1,-3) C(-2,1)
a/ cm A,B,C là 3 đỉnh 1 tam giác
b/ tìm tọa độ trực tâm H,tâm I tâm đường tròn ngoại tiếp và tâm J tâm đường tròn nội tiếp tam giác ABC
c/ TÌM TỌA ĐỘ ĐIỂM M SAO cho
MA+MB min
MB+MC min
MA-MC max
1
123456784
[toán đại 10] phương trình
1) $\frac{2mx^2-m^2+m-2}{x^2-m}=1$
2) Định m để phương trình :
$(mx+2)(x+1)=(mx+m^2)$ có nghiệm duy nhất
3)Định m để phương trình:
$(m^2+2m-3)x=m-1$ có tập nghiệm là R
1) $\frac{2mx^2-m^2+m-2}{x^2-m}=1$
2) Định m để phương trình :
$(mx+2)(x+1)=(mx+m^2)$ có nghiệm duy nhất
3)Định m để phương trình:
$(m^2+2m-3)x=m-1$ có tập nghiệm là R
C
congtubannong123
Câu 1: Không thấy yêu cầu đề bài !
Câu 2: Khai triển VT và VP ta được :
[tex]mx^2+mx+2x+2=mx+m^2[/tex]
\Leftrightarrow [tex]mx^2 + 2x + m^2 - 2[/tex] =0 (*)
Xét với m=0 thì pt (*) trở thành : 2x-2=0 \Leftrightarrow x=2 (1)
Xét với m #0 thì ta có :
[tex] \Delta '=1-m ( m^2 - 2) = 1-m^3+2m [/tex]
Để pt đã cho có nghiệm duy nhất thì pt (*) cũng có nghiệm duy nhất khi :[tex] \Delta'[/tex] =0
\Leftrightarrow [tex] -m^3 + 2m +1 = 0 [/tex] \Leftrightarrow: m=-1 hoặc [tex]m=\frac{1+\sqrt[2]{5}}{2}[/tex] hoặc [tex]m=\frac{1-\sqrt[2]{5}}{2}[/tex]
Từ (1) và (2) \Rightarrow KL
Câu 3:
Pt có tập nghiệm trên R thì khi đó
[tex]m^2+2m-3#0[/tex] và m-1 #0 \Rightarrow m#1
:khi (59): TOÁN GÌ MÀ DỄ THẾ!
Câu 2: Khai triển VT và VP ta được :
[tex]mx^2+mx+2x+2=mx+m^2[/tex]
\Leftrightarrow [tex]mx^2 + 2x + m^2 - 2[/tex] =0 (*)
Xét với m=0 thì pt (*) trở thành : 2x-2=0 \Leftrightarrow x=2 (1)
Xét với m #0 thì ta có :
[tex] \Delta '=1-m ( m^2 - 2) = 1-m^3+2m [/tex]
Để pt đã cho có nghiệm duy nhất thì pt (*) cũng có nghiệm duy nhất khi :[tex] \Delta'[/tex] =0
\Leftrightarrow [tex] -m^3 + 2m +1 = 0 [/tex] \Leftrightarrow: m=-1 hoặc [tex]m=\frac{1+\sqrt[2]{5}}{2}[/tex] hoặc [tex]m=\frac{1-\sqrt[2]{5}}{2}[/tex]
Từ (1) và (2) \Rightarrow KL
Câu 3:
Pt có tập nghiệm trên R thì khi đó
[tex]m^2+2m-3#0[/tex] và m-1 #0 \Rightarrow m#1
:khi (59): TOÁN GÌ MÀ DỄ THẾ!
Last edited by a moderator:
T
toilamanck
Hình học không biet lop mayCho đường tròn (O,R) và 2 điểm P, Q cố định. P nằm ngoài (O) còn Q là điể
Cho đường tròn
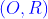và
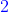điểm
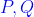cố định.
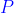nằm ngoài
còn
là điểm nằm trong
. Dây cung di động
của
luôn đi qua
;
lần lượt giao lần thứ hai với
tại
và
.
Chứng minh đường thằng
luôn đi qua
điểm cố định.
Cho đường tròn
Chứng minh đường thằng
N
noinhobinhyen
Gợi ý
tính số các số mà có mặt số 1 và số 2
tính số các số mà số 1 và 2 đứng cạnh nhau
Trừ đi là ra
tính số các số mà có mặt số 1 và số 2
tính số các số mà số 1 và 2 đứng cạnh nhau
Trừ đi là ra
- Status