Bài 1:
Cho tam giác ABC. Các điểm M, N, P lần lượt chia các đoạn thẳng AB, BC, CA theo các tỉ số lần luot là m, n, p( đều khác 1). Chứng minh rằng:
a) M, N, P thẳng hàng khi và chỉ khi mnp = 1 (Định lý Mê- nê- la -uyt)
b) AN, CM, BP đồng quy hoặc song song khi và chỉ khi mnp = -1( Định lý Xê - va)
Phát biểu lại cho dễ gọi nhé.
1.Định lý Menelaus:
ĐL: Cho tam giác ABC và 3 điểm [tex]A^{'},B^{'},C^{'}[/tex] trên các đường thẳng chứa các cạnh BC,CA,AB sao cho : hoặc cả 3 điểm [tex]A^{'},B^{'},C^{'}[/tex] đều nằm trên phần kéo dài của ba cạnh, hoặc một trong ba điểm đó nằm trên phần kéo dài của một cạnh còn hai điểm kia nằm trên hai cạnh của tam giác.
Điều kiện cần và đủ để [tex]A^{'},B^{'},C^{'}[/tex] thẳng hàng là ta có hệ thức.
[tex]\frac{AB^{'}}{B^{'}C}.\frac{CA^{'}}{A^{'}B}.\frac{BC^{'}}{C^{'}A}[/tex] (1)
Chứng Minh.
*) Điều kiện cần : [tex]A^{'},B^{'},C^{'}[/tex] thẳng hàng [TEX]\Rightarrow[/TEX] (1)
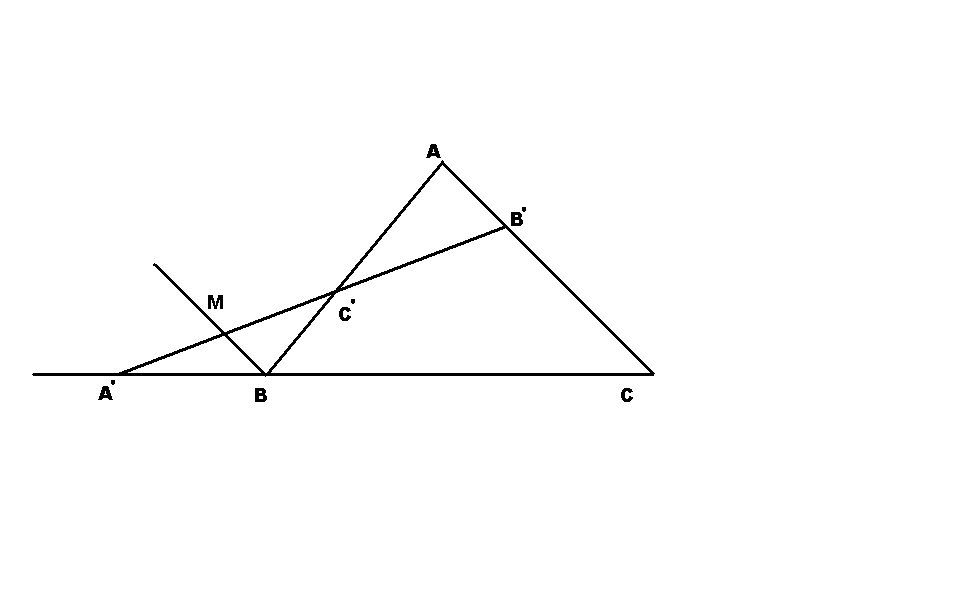
Ta xét trường hợp hai điểm ( B',C' ) nằm trên hai cạnh của tam giác, còn điểm A' nằm trên phần kéo dài của BC.
Từ B kẻ đường thẳng song song với AC cắt A'B' tại M.
Áp dụng định lý thalet có:
[tex]\frac{CA'}{A'B}=\frac{B'C}{BM} \\ \frac{BC'}{C'A}=\frac{BM}{AB'}[/tex]
Nhân từng vế hai đẳng thức trên ta được
[tex]\frac{CA'}{A'B}.\frac{BC'}{C'A}=\frac{B'C}{A'B}[/TEX]
hay [tex]\frac{AB^{'}}{B^{'}C}.\frac{CA^{'}}{A^{'}B}.\frac{BC^{'}}{C^{'}A}=1[/tex]
**) Điều kiện đủ:
Giả sử B',C' nằm trên hia cạnh của tam giác còn A' nằm trên cạnh kéo dài của BC, và có hệ thức (1).
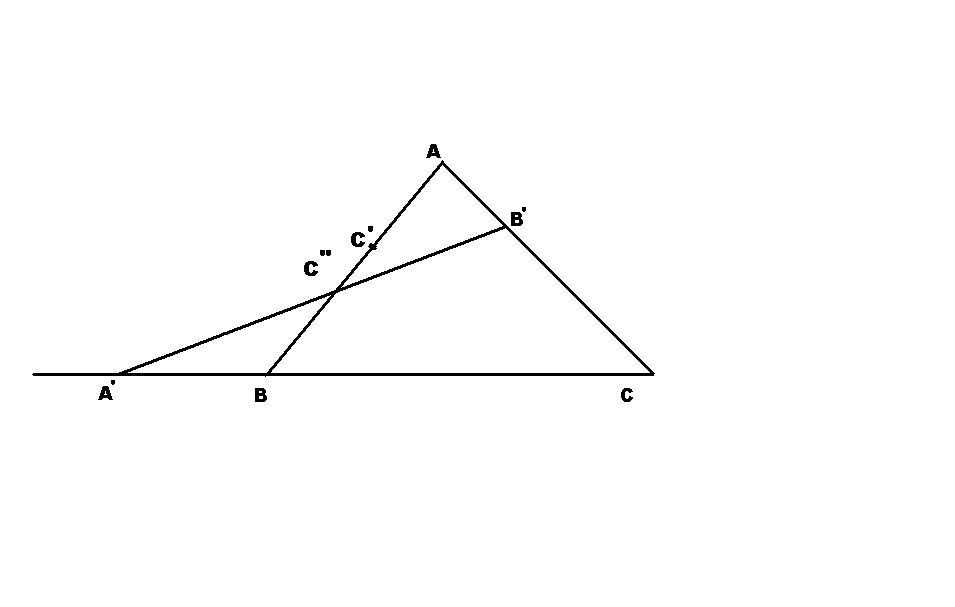
Nếu C' không nằm trên đường thẳng A'B' và A'B' cắt AB tại C" thì, theo điều kiện cần ,ta có:
[tex]\frac{AB'}{B'C}.\frac{CA'}{A'B}.\frac{BC"}{C"A}=1[/tex] (2)
Từ (1)và (2) suy ra:
[tex]\frac{BC'}{C'A}=\frac{BC"}{C"A}[/tex]
Vậy[tex] C^{''}\equiv C'[/tex] ( do C" và C" đều nằm trên AB), và 3 điểm A',B',C' thẳng hàng.
Trường hợp còn lại chứng minh tương tự.