B
B
bigbang195
B
bigbang195
Q
quyenuy0241
Đề bài đúng :
cho a,b,c là độ dài của 3 cạnh 1 tam giác. chứng minh rằng :
[tex] \Leftrightarrow a^3+b^3+c^3-3abc \ge 2a(b-c)^2 +2 b(a-c)^2+2c(a-b)^2 [/tex]
[tex] \Leftrightarrow (a+b-3c)(a-b)^2+(b+c-3a)(b-c)^2+(a+c-3b)(a-c)^2 \ge 0 [/tex]
Do a,b,c là 3 cạnh 1 tam giác nên: [tex] \frac{a-c}{a-b} \ge \frac{b}{c} [/tex]
vậy ta cần CM: [tex]b^2(a+c-3b)+c^2(a+b-3c) \ge 0 [/tex]
[tex] \Leftrightarrow a(b^2+c^2)+bc(c+b) \ge 3(b^3+c^3) [/tex]
B
bigbang195
Chúng ta còn có thể dùng phân tích sau:
BDT tương đương :
(a-b)(a-c)%20\ge%200)
BDT này là dạng Vonicur trong tam giác . Nó chặt hơn BDT
^3)
BDT tương đương :
BDT này là dạng Vonicur trong tam giác . Nó chặt hơn BDT
N
nhockthongay_girlkute
là các số thực dương. Chứng minh rằng :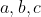
bình phương đưa về
[TEX] (ab+bc+ac)(xy+yz+xz) \geq abx^2+bcy^2+caz^2 [/TEX]
trong đó [TEX] a+b =x^2 , b+c =y^2 ,c+a=z^2 [/TEX]
đến đây tớ k nghĩ dc nữa?
B
bigbang195
L
lucmachthankiem
Dòng đầu tiên anh nhầm dấu.
Còn cái [tex] \frac{a-c}{a-b} \ge \frac{b}{c} [/tex] em không hiểu? Nếu b<a<c thì làm sao đc nhỉ?
B
bigbang195
Có lẽ là thiếu giả sử
N
nhockthongay_girlkute
cho x,y,z >0
[TEX] xy+yz+xz=1 [/TEX]
CM
[TEX] \sum \frac{1}{\sqrt{1+(2x-y)^2}} \leq \frac{3\sqrt{3}}{2}[/TEX]
[TEX] xy+yz+xz=1 [/TEX]
CM
[TEX] \sum \frac{1}{\sqrt{1+(2x-y)^2}} \leq \frac{3\sqrt{3}}{2}[/TEX]
W
williamdunbar
B
bigbang195
Đây chính là BDT AM-GM mà :|
[TEX]\sum_{cyc} \frac{1}{a} \ge \frac{3}{\sqrt[3]{abc}[/TEX]
[TEX]9+\sum_{cyc}a^2b^2 \ge 12\sqrt[3]{abc}[/TEX]
B
bigbang195
N
nhockthongay_girlkute
đặt [TEX] 2x-y =a ; 2y-z=b;2z-x=c [/TEX]
[TEX]=> a+b+c=x+y+z >0 [/TEX]
từ [TEX]ab+bc+ac =1 [/TEX]
ta có
[TEX]14(a^2+b^2+c^2)+35(ab+bc+ac) =49[/TEX]
[TEX]=> 3[14(a^2+b^2+c^2)+35(ab+bc+ac)] \leq 49(a+b+c)^2 [/TEX]
[TEX]=> a+b+c \geq \sqrt{3} [/TEX]
[TEX]BDT <=> \sum \frac{1}{\sqrt{a^2+1}} \leq \frac{3\sqrt{3}}{2} [/TEX]
đây là bài cậu đố đấy ! nhưng tớ chưa nghĩ ra cách giải ! cậu post tiếp giải hộ với :-SS
N
nhockthongay_girlkute
là các số thực dương. Chứng minh rằng :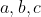
cậu post giải bài này luôn hộ với !nghĩ mãi chẳng ra:-SS:-SS:-SS:-SS
B
bigbang195
D
dandoh221
latex đã bị lỗi, từ nay tớ khuyên mọi người nên gõ bộ tex chính của diễn đàn. trước kia tớ cũng làm vậy nhưng rồi thấy k tiết kiệm đc nhiều thời gian, với lại cũng khó trình bày.
L
legendismine
Theo bất đẳng thức Am-Gm ta có:chovà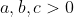
. Chứng minh rằng :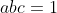
[tex](\sum_{cyc}(ab)^2)^2\ge 3a^2b^2c^2(a^2+b^2+c^2)=3(a^2+b^2+c^2)[/tex]
Lấy căn hai vế ta có dpcm đẳng thức xảy ra khi a=b=c
Last edited by a moderator:
H
hatran04sh03cnsh
[tex]\tex{xet ham so}\\\f(x)=\sqrt{3+x^2}+log_3x+sin(\pi+x)[/tex]
@};-@};-@};-@};-
Last edited by a moderator:
0