N
B
bigbang195
V
vodichhocmai
thỏa mãn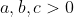
. Chứng minh :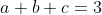
(2b^2+1)(2c^2+1)%20\ge%2027abc)
Chúng ta luôn có[TEX]\ \ \huge\blue 1\ \ [/TEX]điều thật dễ là .
[TEX]\huge\blue ln\(2a^2+1\)-ln\(3a\) \ge \frac{a-1}{3}\ \ \ \ \forall 0<a<3[/TEX]
[TEX]\huge\red \righ Done!![/TEX]
V
vodichhocmai
Xưa thật là xưa
Cho [TEX]x,y,z\in [1;2\][/TEX] Chứng minh rằng khi đó ta có :
[TEX]\(x+y+z\)\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\) \ge 6\(\frac{x}{y+z}+\frac{y}{z+z}+\frac{z}{x+y}\)[/TEX]
Cho [TEX]x,y,z\in [1;2\][/TEX] Chứng minh rằng khi đó ta có :
[TEX]\(x+y+z\)\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\) \ge 6\(\frac{x}{y+z}+\frac{y}{z+z}+\frac{z}{x+y}\)[/TEX]
Last edited by a moderator:
L
lam10495
Giải dùm mình mấy bài này với :
1) Cho a,b [tex]\ge\[/tex] 1 . CMR a[tex]\sqrt{b-1}[/tex] + b[tex]\sqrt{a-1}[/tex] [tex]\le[/tex] ab
2) Cho 3 số dương a , b , c . c/m (a+b)(b+c)(c+a) [tex]\ge\[/tex] 8abc
3) Cho 3 số dương a , b ,c . c/m [tex]\frac{a}{bc} + \frac{b}{ca} + \frac{a}{ab}[/tex] [tex]\ge[/tex] [tex]\frac{1}{a} + \frac {1}{b} + \frac{1}{c}[/tex]
4) Tìm GTNN của hs y = 2x + [tex]\frac{3}{x + 2 }[/tex] khi x > -2
1) Cho a,b [tex]\ge\[/tex] 1 . CMR a[tex]\sqrt{b-1}[/tex] + b[tex]\sqrt{a-1}[/tex] [tex]\le[/tex] ab
2) Cho 3 số dương a , b , c . c/m (a+b)(b+c)(c+a) [tex]\ge\[/tex] 8abc
3) Cho 3 số dương a , b ,c . c/m [tex]\frac{a}{bc} + \frac{b}{ca} + \frac{a}{ab}[/tex] [tex]\ge[/tex] [tex]\frac{1}{a} + \frac {1}{b} + \frac{1}{c}[/tex]
4) Tìm GTNN của hs y = 2x + [tex]\frac{3}{x + 2 }[/tex] khi x > -2
Last edited by a moderator:
D
dandoh221
1.[TEX]b^2 \ge 4b-4[/TEX]
[TEX]\Rightarrow b \ge 2\sqrt{b-1}[/TEX]
[TEX]\Rightarrow \frac{\sqrt{b-1}}{b} \le \frac{1}{2}[/TEX]
Tương tự \Rightarrow đpcm
2. [TEX]a+b \ge 2\sqrt{ab}[/TEX]
[TEX]b+c \ge 2\sqrt{bc}[/TEX]
[TEX]c+a \ge 2\sqrt{ca}[/TEX]
[TEX]\Rightarrow (a+b)(b+c)(c+a) \ge 2\sqrt{ab}.2\sqrt{bc}2.\sqrt{ca} = 8abc[/TEX]
3/[TEX]\frac{a}{bc} + \frac{b}{ca} \ge \frac{2}{c}[/TEX]
làm 2 cái tương tự rồi cộng lại \Rightarrow đpcm
4.y = 2x +\frac{3}{x + 2 } = 2x +4+\frac{3}{x + 2 } -4 \ge 2\sqrt{6}-4
Dấu = xảy ra khi 2(x+2)^2 = 3 ....
Nhớ thời mới học bdt
Last edited by a moderator:
B
bigbang195
W
williamdunbar
V
vodichhocmai
[TEX]\red \huge \frac{a^3}{a^2+b^2}\ge a-\frac{b}{2} \ \ [/TEX]
Last edited by a moderator:
D
donghxh
Dễ dàng chứng minh dc bdt trên như sau:Áp dụng co si ngược dấu
\Leftrightarrow[TEX]a-\frac{ab^2}{a^2+b^2}[/TEX]\geq[TEX]a-\frac{ab^2}{2ab}[/TEX]=[TEX]a-\frac{b}{2}[/TEX]
Tương tự với các bdt # là ra
L
legendismine
V
vodichhocmai
Đặt
ta có bất đẳng thức được viết lại:
+(c+a)}\\\\%20)
[TEX]\Leftrightarrow \frac{1}{2\(a+b\)\(b+c\)\(c+a\)}\sum_{cyc}\[\frac{(b-a)^2}{\(2a+b+c\)\(2b+a+c\)}\]\[ (a+b+c\)(a+b-c)^2+ac\][/TEX]
Khùng luôn
Last edited by a moderator:
S
son_9f_ltv
K
keropik
lâu không vô.
đố mọi ng` chứng minh nesbit=45 cách
Mã:
http://www.mediafire.com/?n4sk1s84sw97xze
B
bigbang195
Bài này dùng kiến thức trong sách giáo khoa thui nha các bạn...
K
keropik
là các số không âm chứng minh rằng :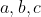
Bài này dùng kiến thức trong sách giáo khoa thui nha các bạn...
Ko đc dùng C-S à?
C-S có trong SGK mà
Sao ra cái đề hay thế
D
daodung28
[TEX]\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\geq3\sqrt[3]{\frac{a}{b}.\frac{b}{c}.\frac{c}{a}=3[/TEX]là các số không âm chứng minh rằng :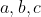
Bài này dùng kiến thức trong sách giáo khoa thui nha các bạn...
D
dandoh221
là các số không âm chứng minh rằng :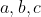
Bài này dùng kiến thức trong sách giáo khoa thui nha các bạn...
Trở thành [TEX]x^3+y^3+z^3 \ge 3xyz[/TEX]
[TEX]\Leftrightarrow (x+y+z)((x-y)^2+(y-z)^2+(z-x)^2) \ge 0[/TEX]
W
williamdunbar
K
keropik
Bạn ơi đề sai dấu bdt rồi fair ngược lại mới đúng!
Ta có:
BPT:
Ma Ta lại thấy
ttự:
\Rightarrowdpcm
Dấu = xr khi a=b=c
@bigbang : sai rồi bạn, xem lại nhá. Đề này sai, đề bạn suy ngược lại cũng sai
@bigbang: vậy cách cm có vde j ko?
Last edited by a moderator: