B
bigbang195
cho a,b,c >0
ab+bc+ac =2abc
CM
[TEX] \sum \frac{1}{a(2a-1)^2} \geq \frac{1}{2}[/TEX]
Vế trái thành :
Last edited by a moderator:
cho a,b,c >0
ab+bc+ac =2abc
CM
[TEX] \sum \frac{1}{a(2a-1)^2} \geq \frac{1}{2}[/TEX]
a,b,c >0 C/m:
[TEX]\sum \frac{a}{\sqrt{a^2+8bc}} \geq 1[/TEX]
a,b,c >0
[TEX] \frac{a+\sqrt{ab}+\sqrt[3]{abc}}{3} \leq \sqrt[3]{a.\frac{a+b}{2}.\frac{a+b+c}{3}} [/TEX]
một bài mạnh hơn
[TEX] a+\sqrt[3]{ab.\frac{a+b}{2}} +\sqrt[3]{abc} \leq 3 \sqrt[3]{a.(\frac{a+b}{2}).( \frac{a+b+c}{3})}[/TEX]
a,b,c >0 C/m:
[TEX]\sum \frac{a}{\sqrt{a^2+8bc}} \geq 1[/TEX]
Cho a,b,c>0 có tổng bằng 3. Tìm max
[tex]a^2b+b^2c+c^2+2(ab^2+bc^2+ca^2)[/tex]
[TEX]\sum \frac{a+2b}{a+2b+3}=\sum \frac{(a+2b)^2}{(a+2b+3)(a+2b)} = \sum \frac{(a+2b)^2}{a^2+4ab+4b^2+3a+6b} \geq \frac{9(\sum a)^2}{5\sum a^2 + 4\sum ab + 9\sum a} (Schwarz)[/TEX]kĩ hơn đc k ....................................................................
Cho các số thực ko âm a, b, c. CM:
[TEX](a^2+b+ \frac{3}{4})(b^2+a+ \frac{3}{4})\geq(2a+\frac{1}{2})(2b+\frac{1}{2})[/TEX]
Chothỏa mãn

Chứng minh rằng :

Đề thi chọn đội tuyển trường THPT ĐAN PHƯỢNG.
Nghĩ mãi không ra :M047:
.....................................................................Bình phương 2 vế ta được:
[TEX]\frac{{2(1-ab)}}{1+ab+a+b}+ 2 \sqrt{\frac{1+ab-a-b}{1+ab+a+b}}[/TEX][TEX] \le \frac{2}{1+a+b}+2\sqrt{\frac{1-(a+b)}{1+a+b}}[/TEX].
Đặt u=ab ; v=a+b
[tex]\Rightarrow \sqrt{\frac{1+u-v}{1+u+v}}-\sqrt{\frac{1-v}{1+v}}\leq \frac{u(2+v)}{(1+v)(1+v+u)}[/tex]
[TEX]\Leftrightarrow \frac{1+u-v}{1+u+v}-\frac{1-v}{1+v}\leq\frac{u(2+v)}{(1+v)(1+v+u)}(\sqrt{\frac{1+u-v}{1+u+v}}+\sqrt{\frac{1-v}{1+v}})[/TEX]
[TEX]\Leftrightarrow \frac{2uv}{(1+u+v)(1+v)}\leq\frac{u(2+v)}{(1+v)(1+v+u)}(\sqrt{\frac{1+u-v}{1+u+v}}+\sqrt{\frac{1-v}{1+v}})[/TEX]
Nếu u=ab=0 thi` BĐT đúng.
Nếu u>0, BĐT tương đương với [TEX]\Leftrightarrow \frac{2v}{2+v}\leq\sqrt{\frac{1+u-v}{1+u+v}}+\sqrt{\frac{1-v}{1+v}}[/TEX]
Ta có:
[TEX]\sqrt{\frac{1+u-v}{1+u+v}}+\sqrt{\frac{1-v}{1+v}}> 2\sqrt{\frac{1-v}{1+v}}=2\sqrt{-1+\frac{2}{1+v}}\geq 2\sqrt{-1+\frac{2}{1+\frac{4}{5}}}=\frac{2}{3}[/TEX]
Ngoài ra: [TEX]\frac{2v}{2+v}=\frac{2}{\frac{2}{v}+1}\leq\frac{2}{3}[/TEX] (do [TEX]0<v=a+b\leq\frac{4}{5}<1[/TEX]).
Từ đó ta có đpcm. =p~
thỏa mãn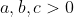 . Chứng minh :
. Chứng minh :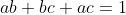

Mạnh hơn chút ít!
[TEX]\sum \frac{a}{\sqrt{a^2+3bc}} \geq \frac{3}{2}[/TEX]
Cho [TEX]a,b,c >0[/TEX] và [TEX]k\geq 8[/TEX]. Chứng minh rằng
[TEX]A:=\frac{a}{\sqrt{a^{2}+kbc}}+\frac{b}{\sqrt{b^{2}+kac}}+\frac{c}{\sqrt{c^{2}+kab}}\geq\frac{3}{\sqrt{1+k}}[/TEX][TEX]k=8[/TEX] chính là đề IMO 42
[TEX]a,b,c\ge 0; \sum a=3. Min: \sum \sqrt{a+3}[/TEX])
)
mạnh hơnLetsuch that .Find the min of :
.Find the min of :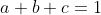

TÌm min bik a,b,c>0 a+b+c=1
[tex]\frac {1}{1-2(ab+bc+ca)}+\frac {1}{abc}[/tex]
[tex]\frac {81}{81(a^2+b^2+c^2)}+\sum_{cyc}\frac {2}{162ab}\ge \frac{(9+3\sqrt {2})^2}{81}[/tex] tự xử vậyLetsuch that .Find the min of :
.Find the min of :