L
letrang3003
Cho a,b,c>0 ab+bc+ca=1/3 C/m:
[tex]\sum_{cyc}\frac {a}{a^2-bc+1}\ge \frac {1}{a+b+c}[/tex]
Last edited by a moderator:
Cho a,b,c>0 ab+bc+ca=1/3 C/m:
[tex]\sum_{cyc}\frac {a}{a^2-bc+1}\ge \frac {1}{a+b+c}[/tex]
1) cho a,b,c>0 ,a+b+c =1
CM
[TEX] \sum \frac{a}{b} + 4(\sum \sqrt{ab}) \geq 7 [/TEX]
2) cho a,b,c >0
CM
[TEX] a+b+c +\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+15 \geq 4(\frac{a}{b}+\frac{b}{c}+\frac{c}{a})[/TEX]
một bài nhẹ nhàng
cho a,b,c là 3 cạnh tam giác
CM
[TEX] \sum \frac{a}{3a-b+c} \geq 1[/TEX]
[TEX]\leftrightarrow[/TEX] [TEX]\sum\frac{2a}{3a-b+c} \ge 2[/TEX]một bài nhẹ nhàng
cho a,b,c là 3 cạnh tam giác
CM
[TEX] \sum \frac{a}{3a-b+c} \geq 1[/TEX]
tổng quát của IMO 2008
cho x,y,z là các số thực khác 1 , xyz =1 , m bất kì
Cm
[TEX] \sum( \frac{x+m}{x-1})^2 \geq 1[/TEX]
cho a,b,c >0
CM
[TEX] \frac{abc}{(a+b)(b+c)(c+a)} \leq \frac{(a+b)(a+b+2c)}{(3a+3b+2c)^2}[/TEX]
(chỉ AM-GM)
Đặt [TEX]a+b=x;b+c=y;c+a=z[/TEX] chắc sẽ đơn giản hơn một ít ...............:-SScho a,b,c >0
CM
[TEX] \frac{abc}{(a+b)(b+c)(c+a)} \leq \frac{(a+b)(a+b+2c)}{(3a+3b+2c)^2}[/TEX]
(chỉ AM-GM)
THTT:
[tex]a,b,c>0 ,T/m: ab+bc+ac=3 \\ CMR: \frac{1}{abc}+\frac{4}{(x+y)(y+z)(z+x)} \ge \frac{3}{2} [/tex]
Nhầm :">
S.O.S
.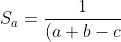(a+c-b)}%20-%20\frac{1}{ab+bc+ac})
...

