- 23 Tháng bảy 2016
- 1,123
- 1,495
- 344
- 23
- Đắk Nông
Ok!!Mai sẽ là chuyên đề hình học nhé các bạn ^^.Lại một lần nữa bạn ghost dragon lại gánh bài tập ^^.
mò ra m=3/2.^^Giúp em bài này với:
Cho:
:y=2x^2)
:y=mx+2-m)
Tìm m để (d) giao với (P) tại 2 điểm A, B sao chovuông tại O
Giúp em bài này với:
Cho:
:y=2x^2)
:y=mx+2-m)
Tìm m để (d) giao với (P) tại 2 điểm A, B sao chovuông tại O
Tính $OA,OB,AB$ theo $m$.Muốn cái đó vuông thì $OA^2+OB^2=AB^2$.
Đó là 1 cách.
Đây là đề thi toán điều kiện chuyên sư phạm năm nay. Khó ở chỗ chậm dần đều :vNT của ta ko cho đủ thời gian. Bài này hay nè đang đúng chủ đề.
https://diendan.hocmai.vn/threads/giai-toan-theo-cach-lap-pt-va-he-phuong-trinh.618147/
Còn bài nào nữa ko? Mấy đề năng khiếu mình giải cũng dcBài ở trên từ điều kiện ở đề bài thì ta sẽ có:$-8t+a=0$(Đi chậm dần đều nên $v=0$) và $-4t^2+at=16$.Giải ra tìm $a$ từ đó suy ra quãng đường AB.
Bài 10 nhaMột bài về dạng biện luận các bạn coi thử nhé!!
Bài 10: (Sưu tầm)
Cuối học kỳ I, một học sinh có hơn 11 bài kiểm tra đạt các điểm $8,9,10$. Biết tổng số điểm các bài kiểm tra đó là $100$. Hỏi học sinh đó có bao nhiêu bài kiểm tra đạt điểm $8,9,10$
Và một bài tiếp tục về vận tốc của chuyên sư phạm năm 2014-2015:
Bài 11: Cho quãng đường $AB$ dài $120$km. Lúc $7$ giờ sáng, một xe máy đi từ $A$->$B$. Đi được $\dfrac{3}{4}$ quãng đường xe bị hỏng phải dừng lại sửa mất $10$ phút rồi đi tiếp đến $B$ với vận tốc nhỏ hơn vận tốc lúc đầu là $10$ km/h. Biết xe máy đến B lúc $11$ giờ $40$ phút trưa cùng ngày. Giả sử vận tốc của xe máy trên $\dfrac{3}{4}$ quãng đường ban đầu không thay đổi và vận tốc của xe máy trên $\dfrac{1}{4}$ quãng đường còn lại cũng không thay đổi. Hỏi xe máy bị hỏng lúc mấy giờ?
P/s: Chắc có lẽ hoàn thành xong 2 bài này chúng ta cùng chuyển qua hình học nhỉ ^^?
@Ma Long @Thoòng Quốc An @Nữ Thần Mặt Trăng @kingsman(lht 2k2),... chiến nốt nào!!
Bài 10:Một bài về dạng biện luận các bạn coi thử nhé!!
Bài 10: (Sưu tầm)
Cuối học kỳ I, một học sinh có hơn 11 bài kiểm tra đạt các điểm $8,9,10$. Biết tổng số điểm các bài kiểm tra đó là $100$. Hỏi học sinh đó có bao nhiêu bài kiểm tra đạt điểm $8,9,10$
Và một bài tiếp tục về vận tốc của chuyên sư phạm năm 2014-2015:
Bài 11: Cho quãng đường $AB$ dài $120$km. Lúc $7$ giờ sáng, một xe máy đi từ $A$->$B$. Đi được $\dfrac{3}{4}$ quãng đường xe bị hỏng phải dừng lại sửa mất $10$ phút rồi đi tiếp đến $B$ với vận tốc nhỏ hơn vận tốc lúc đầu là $10$ km/h. Biết xe máy đến B lúc $11$ giờ $40$ phút trưa cùng ngày. Giả sử vận tốc của xe máy trên $\dfrac{3}{4}$ quãng đường ban đầu không thay đổi và vận tốc của xe máy trên $\dfrac{1}{4}$ quãng đường còn lại cũng không thay đổi. Hỏi xe máy bị hỏng lúc mấy giờ?
P/s: Chắc có lẽ hoàn thành xong 2 bài này chúng ta cùng chuyển qua hình học nhỉ ^^?
@Ma Long @Thoòng Quốc An @Nữ Thần Mặt Trăng @kingsman(lht 2k2),... chiến nốt nào!!
Giải:Một bài về dạng biện luận các bạn coi thử nhé!!
Bài 10: (Sưu tầm)
Cuối học kỳ I, một học sinh có hơn 11 bài kiểm tra đạt các điểm $8,9,10$. Biết tổng số điểm các bài kiểm tra đó là $100$. Hỏi học sinh đó có bao nhiêu bài kiểm tra đạt điểm $8,9,10$
Và một bài tiếp tục về vận tốc của chuyên sư phạm năm 2014-2015:
Bài 11: Cho quãng đường $AB$ dài $120$km. Lúc $7$ giờ sáng, một xe máy đi từ $A$->$B$. Đi được $\dfrac{3}{4}$ quãng đường xe bị hỏng phải dừng lại sửa mất $10$ phút rồi đi tiếp đến $B$ với vận tốc nhỏ hơn vận tốc lúc đầu là $10$ km/h. Biết xe máy đến B lúc $11$ giờ $40$ phút trưa cùng ngày. Giả sử vận tốc của xe máy trên $\dfrac{3}{4}$ quãng đường ban đầu không thay đổi và vận tốc của xe máy trên $\dfrac{1}{4}$ quãng đường còn lại cũng không thay đổi. Hỏi xe máy bị hỏng lúc mấy giờ?
P/s: Chắc có lẽ hoàn thành xong 2 bài này chúng ta cùng chuyển qua hình học nhỉ ^^?
@Ma Long @Thoòng Quốc An @Nữ Thần Mặt Trăng @kingsman(lht 2k2),... chiến nốt nào!!
Để ý ngay câu đề bài:Cuối học kỳ I, một học sinh có hơn 11 bài kiểm tra đạt các điểm $8,9,10$ nên phải có ít nhất một bài kiểm tra đạt điểm $8,9,10$ mỗi loại do đó chỉ có mỗi kết quả $b=2,c=1,a=9$ là thỏa mãn.Giải:
Bài 10:
Ta có: $a+b+c>11$
[tex]100=8a+9b+10c>8(a+b+c)\Rightarrow 11<a+b+c<13[/tex]
Suy ra $a+b+c=12$
$100=8(a+b+c)+b+2c=96+b+2c$
Suy ra
[tex]b+2c=4 \Rightarrow b=2,c=1,a=9[/tex]
Tính ra bài như này đáp án $a=8,b=4,c=0$ và $a=10,b=0,c=2$ cũng ko thấy sai.
Đáp án câu 1:HÌNH HỌC
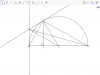
Bài 1: (Đề tuyển sinh lớp 10 THPT, Tỉnh Bình Thuận 2015-2016)
Cho nửa đường tròn tâm $O$ đường kính $AB=2R$, $D$ là một điểm tùy ý trên nửa đường tròn ($D$ khác $A$ và $D$ khác $B$). Các tiếp tuyến với nửa đường tròn (O) tại $A$ và $D$ cắt nhau tại $C$, $BC$ cắt nửa đường tròn $(O)$ tại điểm thứ hai là $E$. Kẻ $DF$ vuông góc với $AB$ tại $F$.
a)Chứng minh: Tứ giác $OACD$ nội tiếp.
b)Chứng minh:$CD^2=CE.CB$.
c)Chứng minh:Đường thẳng $BC$ đi qua trung điểm của $DF$.
d)Giả sử $OC=2R$, tính diện tích phần tam giác $ACD$ nằm ngoài nửa đường tròn $(O)$ theo $R$.
View attachment 10293
Lời giải bài 2:
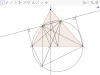
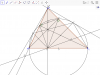
Bài 2: (Đề tuyển sinh lớp 10 THPT,TP Hồ Chí Minh 2015-2016)
Cho tam giác $ABC (AB<AC)$ có ba góc nhọn. Đường tròn tâm $O$ đường kính $BC$ cắt các cạnh $AC, AB$ lần lượt tại $E, F$. Gọi $H$ là giao điểm của $BE$ và $CF$. $D$ là giao điểm của $AH$ và $BC$.
a) Chứng minh : $AD$ vuông góc $BC$
b) Chứng minh $EFDO$ là tứ giác nội tiếp
c) Trên tia đối của tia $DE$ lấy điểm $L$ sao cho $DL = DF$. Tính số đo $\widehat{BLC}$.
d) Gọi $R, S$ lần lượt là hình chiếu của $B,C$ lên $EF.$ Chứng minh $DE + DF = RS$
View attachment 10294

