Bài 4:Đề thi tuyển sinh lớp 10 THPT, Tỉnh Bình Định 2015-2016
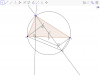
Cho tam giác ABC(AB<AC)ABC(AB<AC)ABC(AB333 góc nhọn nội tiếp trong đường tròn (O;R)(O;R)(O;R). Vẽ đường cao AHAHAH của tam giác ABCABCABC, đường kính ADADAD của đường tròn. Gọi E,FE,FE,F lần lượt chân đường vuông góc kẻ từ CCC và BBB xuống đường thẳng ADADAD. MMM là trung điểm của BCBCBC.
a) Chứng minh :ABHFABHFABHF,BMOFBMOFBMOF là tứ giác nội tiếp.
b) Chứng minh :HE//BDHE//BDHE//BD.
c) Chứng minh :SABC=AB.AC.BC4RSABC=AB.AC.BC4RS_{ABC}=\dfrac{AB.AC.BC}{4R}
a) Có: [tex]\widehat{AFB} = 90 ^{\circ} (BF \perp AD ); \widehat{AHB} = 90 ^{\circ} (AH \perp BC)[/tex]
=> Tứ giác ABHF nội tiếp
Trong (O) có M là trung điểm của dây BC
=> [tex]OM \perp BC \Rightarrow \widehat{BMO} = 90 ^{\circ}[/tex]
Lại có: [tex]\widehat{BFO} = 90 ^{\circ} (BF \perp AD)[/tex]
Có: [tex]\widehat{BMO} + \widehat{BFO} = 90 ^{\circ} + 90 ^{\circ} = 180 ^{\circ}[/tex]
do đó: Tứ giác BMOF nội tiếp
b) Có: [tex]\widehat{CBD} = \widehat{DAC} ( = \frac{1}{2}[/tex] sđ cung DC)
Lại có: [tex]\widehat{AHC} = 90 ^{\circ} ( AH \perp BC ) ; \widehat{AEC} = 90 ^{\circ} ( CE \perp AD )[/tex]
=> Tứ giác AHEC nội tiếp
=> [tex]\widehat{EAD} = \widehat{CHA}[/tex]
Do đó : [tex]\widehat{CBD} = \widehat{CHE} \Rightarrow HE // BD[/tex]
c) Xét [tex]\Delta ABD[/tex] và [tex]\Delta AHC[/tex]
Có [tex]\widehat{ABD} = 90 ^{\circ}[/tex] (góc nội tiếp chắn nửa đường tròn)
[tex]\widehat{AHC} = 90 ^{\circ} ( AH \perp BC)[/tex]
[tex]\widehat{ACB} = \widehat{ADB} ( = \frac{1}{2}[/tex] sđ cung AB)
[tex]\Rightarrow \Delta ABD \sim \Delta AHC[/tex]
[tex]\Rightarrow \frac{AB}{AH} = \frac{AD}{AC} \Rightarrow AB . AC = AH . AD[/tex]
[tex]\Rightarrow AH = \frac{AB . AC}{2 R}[/tex]
[tex]S_{ABC} = \frac{AH . BC}{2} = \frac{AB . AC . BC}{4 R}[/tex]
https://diendan.hocmai.vn/attachments/upload_2017-6-3_17-1-5-png.10363/
Chuẩn rồi đó bạn. Quất tiếp bài nữa được không :v