buồn ké là @Nguyễn Xuân Hiếu cần tối này công báo đạp án vì ngoài bài này các bài còn lại cơ bản đã giải xongOa.Buồn qué ^^.Mọi người ở trên đều sai bài 1c rồi nhé.Các bạn đều quên rằng:
$2x>\sqrt{4x-1}$ chắc gì VT đã dương mà bình phương.Lần sau mong mọi người cẩn thẩn lại nhé.
Hướng dẫn:Điều kiện sẽ là:
$\left\{\begin{matrix}
&4x \geq 1(1) \\
&2x>\sqrt{4x-1}(2)
\end{matrix}\right.$.
Giải 1 thì sẽ được $ x \geq \dfrac{1}{4}$.
Do đó $x$ dương rồi nên có thể bình phương 2 vế ở (2)
Sau khi bình phương 2 vế sẽ được $(2x-1)^2>0 \Rightarrow x \neq \dfrac{1}{2}$.
Vậy điều kiện xác định sẽ là :$x \geq \dfrac{1}{4}$ và $ x\neq \dfrac{1}{2}$.
@huonggiangnb2002 @Nữ Thần Mặt Trăng @kingsman(lht 2k2) @Phạm Linh
Toán [Thảo luận] Topic ôn tập thi tuyển sinh vào lớp 10
- Thread starter iceghost
- Ngày gửi
- Replies 159
- Views 27,048
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
- 20 Tháng chín 2013
- 5,018
- 7,484
- 941
- TP Hồ Chí Minh
- Đại học Bách Khoa TPHCM
Bài 2e của mình làm khó mọi người rồi nhỉ ? Mình xin công bố đáp án nhé
= \left[\sqrt{\left(5-3\sqrt{2}\right) + 2\sqrt{\left(5-3\sqrt{2}\right)\left(3\sqrt{2}-4\right)} + \left(3\sqrt{2}-4\right)} - \sqrt{5-3\sqrt{2}}\right] : \left(\sqrt{3\sqrt{2}-4}\right) \\
= \left[\sqrt{\left(\sqrt{5-3\sqrt{2}} + \sqrt{3\sqrt{2}- 4}\right)^2} - \sqrt{5-3\sqrt{2}}\right] : \left(\sqrt{3\sqrt{2}-4}\right) \\
= \left(\left|\sqrt{5-3\sqrt{2}} + \sqrt{3\sqrt{2} - 4}\right| - \sqrt{5-3\sqrt{2}}\right) : \left(\sqrt{3\sqrt{2}-4}\right) \\
= \left(\sqrt{5-3\sqrt{2}} + \sqrt{3\sqrt{2}-4} - \sqrt{5-3\sqrt{2}}\right) : \left(\sqrt{3\sqrt{2}-4}\right) \\
= \left(\sqrt{3\sqrt{2}-4}\right) : \left(\sqrt{3\sqrt{2}-4}\right) = 1$
Cám ơn các bạn đã ủng hộ topic Mình sẽ đăng chuyên đề mới vào tối hôm nay
Mình sẽ đăng chuyên đề mới vào tối hôm nay
Lời giải. $E=\left(\sqrt{1+2\sqrt{27\sqrt{2}-38}}-\sqrt{5-3\sqrt{2}}\right) : \left(\sqrt{3\sqrt{2}-4}\right) \\Chúng ta cùng bắt đầu bài tập của chương I nào
Bài 2. Rút gọn biểu thức:
e) $E=(\sqrt{1+2\sqrt{27\sqrt{2}-38}}-\sqrt{5-3\sqrt{2}}) : (\sqrt{3\sqrt{2}-4})$
Xem thêm : [Lý thuyết] Topic ôn tập thi tuyển sinh vào lớp 10
= \left[\sqrt{\left(5-3\sqrt{2}\right) + 2\sqrt{\left(5-3\sqrt{2}\right)\left(3\sqrt{2}-4\right)} + \left(3\sqrt{2}-4\right)} - \sqrt{5-3\sqrt{2}}\right] : \left(\sqrt{3\sqrt{2}-4}\right) \\
= \left[\sqrt{\left(\sqrt{5-3\sqrt{2}} + \sqrt{3\sqrt{2}- 4}\right)^2} - \sqrt{5-3\sqrt{2}}\right] : \left(\sqrt{3\sqrt{2}-4}\right) \\
= \left(\left|\sqrt{5-3\sqrt{2}} + \sqrt{3\sqrt{2} - 4}\right| - \sqrt{5-3\sqrt{2}}\right) : \left(\sqrt{3\sqrt{2}-4}\right) \\
= \left(\sqrt{5-3\sqrt{2}} + \sqrt{3\sqrt{2}-4} - \sqrt{5-3\sqrt{2}}\right) : \left(\sqrt{3\sqrt{2}-4}\right) \\
= \left(\sqrt{3\sqrt{2}-4}\right) : \left(\sqrt{3\sqrt{2}-4}\right) = 1$
Cám ơn các bạn đã ủng hộ topic
- 20 Tháng chín 2013
- 5,018
- 7,484
- 941
- TP Hồ Chí Minh
- Đại học Bách Khoa TPHCM
Bài này chỉ có thể khử căn ở mẫu chứ không rút gọn được biểu thức trong căn lớn nhé bạnGiúp mk bài này với. Phân tích ra nó cứ kì kì:
Tính giá trị biểu thức:
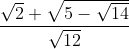
$\dfrac{\sqrt{2} + \sqrt{5-\sqrt{14}}}{\sqrt{12}} = \dfrac{\sqrt{3}(\sqrt{2}+\sqrt{5-\sqrt{14}})}{\sqrt{3} \cdot \sqrt{12}} = \dfrac{\sqrt{6} + \sqrt{15 - 3\sqrt{14}}}{6}$
Ok bạn mk cũng ra vậy nhưng thấy nó vẫn còn căn nên tưởng saiBài này chỉ có thể khử căn ở mẫu chứ không rút gọn được biểu thức trong căn lớn nhé bạn
$\dfrac{\sqrt{2} + \sqrt{5-\sqrt{14}}}{\sqrt{12}} = \dfrac{\sqrt{3}(\sqrt{2}+\sqrt{5-\sqrt{14}})}{\sqrt{3} \cdot \sqrt{12}} = \dfrac{\sqrt{6} + \sqrt{15 - 3\sqrt{14}}}{6}$
- 20 Tháng chín 2013
- 5,018
- 7,484
- 941
- TP Hồ Chí Minh
- Đại học Bách Khoa TPHCM
Ta hãy làm tiếp bài tập tự luyện cho chuyên đề tiếp theo nhé !
Cho phương trình $x^2-(2m+1)x+m^2+m-2=0$ ($m$ là tham số ).
a) Giải phương trình (1) khi $m=2$.
b) Tìm $m$ để phương trình (1) có hai nghiệm phân biệt $x_1,x_2$ thõa mãn:$x_1(x_1-2x_2)+x_2(x_2-3x_1)=9$.
Bài 2. (Đề thi tuyển sinh lớp 10 tỉnh Phú Thọ 2013-2014)
Cho phương trình $x^2+2(m+1)x+m^2=0$. Tìm $m$ để phương trình có hai nghiệm phân biệt trong đó có một nghiệm bằng $-2$.
Bài 3. (Đề thi tuyển sinh lớp 10 TP.Hồ Chí Minh 2014-2015)
Cho phương trình $x^2-mx-1=0 \quad (1)$ ($x$ là ẩn số)
a)Chứng minh phương trình $(1)$ luôn có 2 nghiệm trái dấu.
b)Gọi $x_1,x_2$ là các nghiệm của phương trình $(1)$.
Tính giá trị của biểu thức $P=\dfrac{x_1^2+x_1-1}{x_1}-\dfrac{x_2^2+x_2-1}{x_2}$.
Hướng dẫn câu b). Hạ bậc giống bài 3 (tức tính $x_1^2$ theo $x_1$ và $x_2^2$ theo $x_2$) rồi thay vào $P$.
Bài 4. (Sưu tầm)
Tìm $m$ để phương trình $x^2+mx+m-2=0$ có 2 nghiệm $x_1,x_2$ thỏa mãn $|x_1-x_2|=2$.
Hướng dẫn. Ta có $|x_1 - x_2| = 2 \iff (x_1-x_2)^2 = 4$. Khai triển và giải bình thường
Lưu ý. $|x_1 - x_2|$ khác với $(x_1-x_2)$ nên nếu gặp $(x_1-x_2)$ thì ta không thể bình phương hai vế và dùng dấu tương đương được, ta sẽ dùng dấu suy ra và thử lại nghiệm trước khi kết luận.
Bài 5. (Sưu tầm)
Cho phương trình $x^2-mx+(m^2+1)=0$. Tìm giá trị nhỏ nhất của $x_1^2+x_2^2$.
Bài 6. (Đề thi tuyển sinh vào lớp 10 TP.Hồ Chí Minh 2012-2013)
Cho phương trình $x^2-2mx+m-2=0$($x$ là ẩn số)
a) Chứng minh rằng phương trình luôn có nghiệm phân biệt với mọi $m$.
b) Gọi $x_1,x_2$ là các nghiệm của phương trình.
Tìm $m$ để biểu thức $M=\dfrac{-24}{x_1^2+x_2^2-6x_1x_2}$ đạt giá trị nhỏ nhất.
Bài 7. (Đề tuyển sinh TP.Hà Nội 2012-2013)
Cho phương trình $x^2-(4m-1)x+3m^2-2m=0$ (ẩn $x$). Tìm $m$ để phương trình có hai nghiệm phân biệt $x_1,x_2$ thõa mãn điều kiện $x_1^2+x_2^2=7$.
Bài 8. (Đề thi tuyển sinh lớp 10 tỉnh Bình Phước 2014-2015)
Cho phương trình $x^2+mx+1=0 \; (1)$ với $m$ là tham số.
a) Giải phương trình với $m=4$.
b) Tìm giá trị của $m$ để phương trình $(1)$ có hai nghiệm $x_1,x_2$ thõa mãn : $\dfrac{x_1^2}{x_2^2}+\dfrac{x_2^2}{x_1^2}>7$.
Lưu ý câu b. Đối với những dạng bài có mẫu thức như thế này, tốt nhất ta hãy chuyển hết $VP$ qua $VT$ rồi quy đồng hẳn lên, tránh nhầm lẫn chiều bất phương trình trong việc nhân chéo. (Mặc dù trong TH này, nhân chéo vẫn được vì $x_1^2x_2^2 \geqslant 0$ nên không làm đổi chiều bất phương trình)
Bài 9. (Đề thi tuyển sinh lớp 10 TP.Hồ Chí Minh 2013-2014)
Cho phương trinh $8x^2-8x+m^2+1=0 \; (*)$ ($x$ là ẩn số).
a) Định $m$ để phương trình $(*)$ có nghiệm $x=\dfrac{1}{2}$
b) Định $m$ để phương trình $(*)$ có 2 nghiệm $x_1,x_2$ thõa điều kiện: $x_1^4-x_2^4=x_1^3-x_2^3$.
Hướng dẫn câu b. Hạ bậc $x_1^4$ và $x_2^4$ xuống $x_1^3$ và $x_2^3$ và triệt tiêu với VP, sau đó phân tích thành nhân tử là được. (Tính $x^2$ theo $x$, suy ra ta tính được $x^4 = x^2 \cdot x^2$ theo $x \cdot x^2 = x^3$)
Bài 10. (Đề thi tuyển sinh lớp 10 Tỉnh Nam Định 2015-2016)
Cho phương trình $x^2-2(m-1)x+m^2-6=0 \; (1)$ (với $m$ là tham số)
a) Giải phương trình khi $m=3$.
b) Với giá trị nhỏ nhất của $m$ thì phương trình có các nghiệm $x_1,x_2$ thõa mãn $x_1^2+x_2^2=16$
Xem thêm : [Lý thuyết] Topic ôn tập thi tuyển sinh vào lớp 10
Bài tập tự luyện cho chuyên đề 2
Bài 1. (Đề thi tuyển sinh lớp 10 tỉnh Quảng Bình 2015-2016)Cho phương trình $x^2-(2m+1)x+m^2+m-2=0$ ($m$ là tham số ).
a) Giải phương trình (1) khi $m=2$.
b) Tìm $m$ để phương trình (1) có hai nghiệm phân biệt $x_1,x_2$ thõa mãn:$x_1(x_1-2x_2)+x_2(x_2-3x_1)=9$.
Bài 2. (Đề thi tuyển sinh lớp 10 tỉnh Phú Thọ 2013-2014)
Cho phương trình $x^2+2(m+1)x+m^2=0$. Tìm $m$ để phương trình có hai nghiệm phân biệt trong đó có một nghiệm bằng $-2$.
Bài 3. (Đề thi tuyển sinh lớp 10 TP.Hồ Chí Minh 2014-2015)
Cho phương trình $x^2-mx-1=0 \quad (1)$ ($x$ là ẩn số)
a)Chứng minh phương trình $(1)$ luôn có 2 nghiệm trái dấu.
b)Gọi $x_1,x_2$ là các nghiệm của phương trình $(1)$.
Tính giá trị của biểu thức $P=\dfrac{x_1^2+x_1-1}{x_1}-\dfrac{x_2^2+x_2-1}{x_2}$.
Hướng dẫn câu b). Hạ bậc giống bài 3 (tức tính $x_1^2$ theo $x_1$ và $x_2^2$ theo $x_2$) rồi thay vào $P$.
Bài 4. (Sưu tầm)
Tìm $m$ để phương trình $x^2+mx+m-2=0$ có 2 nghiệm $x_1,x_2$ thỏa mãn $|x_1-x_2|=2$.
Hướng dẫn. Ta có $|x_1 - x_2| = 2 \iff (x_1-x_2)^2 = 4$. Khai triển và giải bình thường
Lưu ý. $|x_1 - x_2|$ khác với $(x_1-x_2)$ nên nếu gặp $(x_1-x_2)$ thì ta không thể bình phương hai vế và dùng dấu tương đương được, ta sẽ dùng dấu suy ra và thử lại nghiệm trước khi kết luận.
Bài 5. (Sưu tầm)
Cho phương trình $x^2-mx+(m^2+1)=0$. Tìm giá trị nhỏ nhất của $x_1^2+x_2^2$.
Bài 6. (Đề thi tuyển sinh vào lớp 10 TP.Hồ Chí Minh 2012-2013)
Cho phương trình $x^2-2mx+m-2=0$($x$ là ẩn số)
a) Chứng minh rằng phương trình luôn có nghiệm phân biệt với mọi $m$.
b) Gọi $x_1,x_2$ là các nghiệm của phương trình.
Tìm $m$ để biểu thức $M=\dfrac{-24}{x_1^2+x_2^2-6x_1x_2}$ đạt giá trị nhỏ nhất.
Bài 7. (Đề tuyển sinh TP.Hà Nội 2012-2013)
Cho phương trình $x^2-(4m-1)x+3m^2-2m=0$ (ẩn $x$). Tìm $m$ để phương trình có hai nghiệm phân biệt $x_1,x_2$ thõa mãn điều kiện $x_1^2+x_2^2=7$.
Bài 8. (Đề thi tuyển sinh lớp 10 tỉnh Bình Phước 2014-2015)
Cho phương trình $x^2+mx+1=0 \; (1)$ với $m$ là tham số.
a) Giải phương trình với $m=4$.
b) Tìm giá trị của $m$ để phương trình $(1)$ có hai nghiệm $x_1,x_2$ thõa mãn : $\dfrac{x_1^2}{x_2^2}+\dfrac{x_2^2}{x_1^2}>7$.
Lưu ý câu b. Đối với những dạng bài có mẫu thức như thế này, tốt nhất ta hãy chuyển hết $VP$ qua $VT$ rồi quy đồng hẳn lên, tránh nhầm lẫn chiều bất phương trình trong việc nhân chéo. (Mặc dù trong TH này, nhân chéo vẫn được vì $x_1^2x_2^2 \geqslant 0$ nên không làm đổi chiều bất phương trình)
Bài 9. (Đề thi tuyển sinh lớp 10 TP.Hồ Chí Minh 2013-2014)
Cho phương trinh $8x^2-8x+m^2+1=0 \; (*)$ ($x$ là ẩn số).
a) Định $m$ để phương trình $(*)$ có nghiệm $x=\dfrac{1}{2}$
b) Định $m$ để phương trình $(*)$ có 2 nghiệm $x_1,x_2$ thõa điều kiện: $x_1^4-x_2^4=x_1^3-x_2^3$.
Hướng dẫn câu b. Hạ bậc $x_1^4$ và $x_2^4$ xuống $x_1^3$ và $x_2^3$ và triệt tiêu với VP, sau đó phân tích thành nhân tử là được. (Tính $x^2$ theo $x$, suy ra ta tính được $x^4 = x^2 \cdot x^2$ theo $x \cdot x^2 = x^3$)
Bài 10. (Đề thi tuyển sinh lớp 10 Tỉnh Nam Định 2015-2016)
Cho phương trình $x^2-2(m-1)x+m^2-6=0 \; (1)$ (với $m$ là tham số)
a) Giải phương trình khi $m=3$.
b) Với giá trị nhỏ nhất của $m$ thì phương trình có các nghiệm $x_1,x_2$ thõa mãn $x_1^2+x_2^2=16$
Xem thêm : [Lý thuyết] Topic ôn tập thi tuyển sinh vào lớp 10
- 28 Tháng hai 2017
- 4,472
- 5,490
- 779
- Hà Nội
- THPT Đồng Quan
Bài 1: Lỗi kĩ thuật ở pt thiếu (1) ^^Ta hãy làm tiếp bài tập tự luyện cho chuyên đề tiếp theo nhé !
Bài tập tự luyện cho chuyên đề 2Bài 1. (Đề thi tuyển sinh lớp 10 tỉnh Quảng Bình 2015-2016)
Cho phương trình $x^2-(2m+1)x+m^2+m-2=0$ ($m$ là tham số ).
a) Giải phương trình (1) khi $m=2$.
b) Tìm $m$ để phương trình (1) có hai nghiệm phân biệt $x_1,x_2$ thõa mãn:$x_1(x_1-2x_2)+x_2(x_2-3x_1)=9$.
a) Thay $m=2$ vào pt (1) ta đc:
$x^2-(2.2+1)x+2^2+2-2=0\\\Leftrightarrow x^2-5x+4=0\Leftrightarrow ...$
b)$\Delta =[(2m+1)]^2-4(m^2+m-2)=9>0\\\Rightarrow x_1=m+2;x_2=m-1\\\Rightarrow (m+2)(4-m)-(m-1)(2m+7)=9\\\Leftrightarrow -3m^2-3m+6=0\Leftrightarrow m^2+m-2=0\\\Leftrightarrow (m+2)(m-1)=0\Leftrightarrow m=-2 \ or \ m=1$
P/s: có thể đây là 1 cách làm khác người bởi vì em chưa có học cái này ^^
@iceghost : Cách này vẫn đúng nhé bạn. Nhưng trong trường hợp đề bảo là "b) Không được giải phương trình, hãy tìm $m$ để ..." thì làm thế nào nhỉ ?
Có bạn nào có cách khác không nè
Last edited by a moderator:
bài 4
theo vi -ét có
x1 +x2 = -m
x1*x2 = m-2
[tex]\Delta = m^{2} -4*(m-2)\Leftrightarrow (m-2)^{2} +4> 4\Leftrightarrow (x_{1}-x_{2})^{2} = (x_{1}+x_{2})^{2}-4x_{1}x_{2}\Leftrightarrow m^{2}-4m +8 =4\Leftrightarrow (m-2)^{2}=0\Leftrightarrow m= 2[/tex]
bai này mình tính deta ra đc ko nhỉ @iceghost
Ý bạn là tính denta để tính $x_1,x_2$ theo $m$ hả? @Nguyễn Xuân Hiếu
theo vi -ét có
x1 +x2 = -m
x1*x2 = m-2
[tex]\Delta = m^{2} -4*(m-2)\Leftrightarrow (m-2)^{2} +4> 4\Leftrightarrow (x_{1}-x_{2})^{2} = (x_{1}+x_{2})^{2}-4x_{1}x_{2}\Leftrightarrow m^{2}-4m +8 =4\Leftrightarrow (m-2)^{2}=0\Leftrightarrow m= 2[/tex]
bai này mình tính deta ra đc ko nhỉ @iceghost
Ý bạn là tính denta để tính $x_1,x_2$ theo $m$ hả? @Nguyễn Xuân Hiếu
Last edited by a moderator:
- 28 Tháng hai 2017
- 4,472
- 5,490
- 779
- Hà Nội
- THPT Đồng Quan
Vậy dùng ĐL Vi-ét ạ? (mất nửa tiếng để đọc và hiểu chỗ lý thuyết@iceghost : Cách này vẫn đúng nhé bạn. Nhưng trong trường hợp đề bảo là "b) Không được giải phương trình, hãy tìm $m$ để ..." thì làm thế nào nhỉ ?
Có bạn nào có cách khác không nè
$\Delta =[-(2m+1)]^2-4(m^2+m-2)=9>0$
=> pt (1) luôn có nghiệm phân biệt
Theo ĐL Vi-ét ta có: $\left\{\begin{matrix}x_1+x_2=2m+1\\ x_1x_2=m^2+m-2\end{matrix}\right.$
Khi đó ta có: $x_1(x_1-2x_2)+x_2(x_2-3x_1)=9\\\iff (x_1+x_2)^2-7x_1x_2-9=0\\\iff (2m+1)^2-7(m^2+m-2)-9=0\\\iff -3m^2-3m+6=0\\\iff (m+2)(m-1)=0\\\iff x=-2 \ or \ x=1$
Vậy...
Mà cái chỗ cuối có đc coi là giải pt ko ạ?
Ý của khang là không giải ra cụ thể $x_1,x_2$ mà áp dụng ngay vi-et để lập quan hệ như bạn là ổn rồi.Chứ cái đoạn cuối mà giải phương trình thì vẫn được.Miễn là đừng giải ngay $x_1=....,x_2=....$ là ok.
@Nguyễn Xuân Hiếu
Last edited by a moderator:
được nhé ,, vì phương trình tích cũng dc coi là một dạng phương trình ...........có thể ví dụ như x^2 -1 =0 nếu ta giải bằng cách pt tích cũng cho ra kết quả như giải pt bâcj 2 ko có bxVậy dùng ĐL Vi-ét ạ? (mất nửa tiếng để đọc và hiểu chỗ lý thuyết)
$\Delta =[-(2m+1)]^2-4(m^2+m-2)=9>0$
=> pt (1) luôn có nghiệm phân biệt
Theo ĐL Vi-ét ta có: $\left\{\begin{matrix}x_1+x_2=2m+1\\ x_1x_2=m^2+m-2\end{matrix}\right.$
Khi đó ta có: $x_1(x_1-2x_2)+x_2(x_2-3x_1)=9\\\iff (x_1+x_2)^2-7x_1x_2-9=0\\\iff (2m+1)^2-7(m^2+m-2)-9=0\\\iff -3m^2-3m+6=0\\\iff (m+2)(m-1)=0\\\iff x=-2 \ or \ x=1$
Vậy...
Mà cái chỗ cuối có đc coi là giải pt ko ạ?
- 28 Tháng hai 2017
- 4,472
- 5,490
- 779
- Hà Nội
- THPT Đồng Quan
vậy nếu ko đc giải pt thì làm cách nào vậy bạn?được nhé ,, vì phương trình tích cũng dc coi là một dạng phương trình ...........có thể ví dụ như x^2 -1 =0 nếu ta giải bằng cách pt tích cũng cho ra kết quả như giải pt bâcj 2 ko có bx
Thôi mk hiểu rồi ^^
- 28 Tháng hai 2017
- 4,472
- 5,490
- 779
- Hà Nội
- THPT Đồng Quan
viết nhầm $m$ thành $x$ ^^Vậy dùng ĐL Vi-ét ạ? (mất nửa tiếng để đọc và hiểu chỗ lý thuyết)
$\Delta =[-(2m+1)]^2-4(m^2+m-2)=9>0$
=> pt (1) luôn có nghiệm phân biệt
Theo ĐL Vi-ét ta có: $\left\{\begin{matrix}x_1+x_2=2m+1\\ x_1x_2=m^2+m-2\end{matrix}\right.$
Khi đó ta có: $x_1(x_1-2x_2)+x_2(x_2-3x_1)=9\\\iff (x_1+x_2)^2-7x_1x_2-9=0\\\iff (2m+1)^2-7(m^2+m-2)-9=0\\\iff -3m^2-3m+6=0\\\iff (m+2)(m-1)=0\\\iff x=-2 \ or \ x=1$
Vậy...
Mà cái chỗ cuối có đc coi là giải pt ko ạ?
Ý của khang là không giải ra cụ thể $x_1,x_2$ mà áp dụng ngay vi-et để lập quan hệ như bạn là ổn rồi.Chứ cái đoạn cuối mà giải phương trình thì vẫn được.Miễn là đừng giải ngay $x_1=....,x_2=....$ là ok.
@Nguyễn Xuân Hiếu
giúp mình bài này. Cảm ơn
Cho phương trình [tex]x^{2}[/tex] -2(k-2)x-3k+10=0
Khi phương trình có 2 nghiệm x1, x2 tìm hệ thức giữa x1 và x2 độc lập đối với k
Cho phương trình [tex]x^{2}[/tex] -2(k-2)x-3k+10=0
Khi phương trình có 2 nghiệm x1, x2 tìm hệ thức giữa x1 và x2 độc lập đối với k
thường các bài dạng này mình hay tính denta ..( để làm dk ) ..bài 4
theo vi -ét có
x1 +x2 = -m
x1*x2 = m-2
[tex]\Delta = m^{2} -4*(m-2)\Leftrightarrow (m-2)^{2} +4> 4\Leftrightarrow (x_{1}-x_{2})^{2} = (x_{1}+x_{2})^{2}-4x_{1}x_{2}\Leftrightarrow m^{2}-4m +8 =4\Leftrightarrow (m-2)^{2}=0\Leftrightarrow m= 2[/tex]
bai này mình tính deta ra đc ko nhỉ @iceghost
Ý bạn là tính denta để tính $x_1,x_2$ theo $m$ hả? @Nguyễn Xuân Hiếu
câu này thêm ý câu a : pt luôn có 2 nghiệm phân biệt với mọi nghiệm phân biệt ....để thích hợp hơn
- 20 Tháng chín 2013
- 5,018
- 7,484
- 941
- TP Hồ Chí Minh
- Đại học Bách Khoa TPHCM
Nhưng nếu đề không có câu a và bạn quên tính $\Delta$ để làm điều kiện thì bạn bị trừ điểm, thật "đơn giản" phải không nào.thường các bài dạng này mình hay tính denta ..( để làm dk ) ..
câu này thêm ý câu a : pt luôn có 2 nghiệm phân biệt với mọi nghiệm phân biệt ....để thích hợp hơn
mình tính denta rồi mà ...mình cũng nghĩ hơi kì nhỉ .....nếu có câu a như vậy thì sẽ liền mạch bài toán hơnNhưng nếu đề không có câu a và bạn quên tính $\Delta$ để làm điều kiện thì bạn bị trừ điểm, thật "đơn giản" phải không nào.
giúp mình bài này. Cảm ơn
Cho phương trình [tex]x^{2} -2(k-2)x-3k+10=0[/tex]
Khi phương trình có 2 nghiệm x1, x2 tìm hệ thức giữa x1 và x2 độc lập đối với k
với dạng bài này
B1: tính delta
B2 áp dụng vi ét
S=x1+x2=2(k-2)
P=x1.x2=-3k+10
B3 Tính k theo S
B4 Thế k vào P
ta sẽ đc hệ thức giữa P và S
rồi thay x1 x2 vào
a) Với m = 3 ta có phương trình như sau:Bài 10. (Đề thi tuyển sinh lớp 10 Tỉnh Nam Định 2015-2016)
Cho phương trình x2−2(m−1)x+m2−6=0(1)x2−2(m−1)x+m2−6=0(1)x^2-2(m-1)x+m^2-6=0 \; (1) (với mmm là tham số)
a) Giải phương trình khi m=3m=3m=3.
b) Với giá trị nhỏ nhất của mmm thì phương trình có các nghiệm x1,x2x1,x2x_1,x_2 thõa mãn x21+x22=16x12+x22=16x_1^2+x_2^2=16
[tex]x ^{2} - 2 \left ( 3 - 1 \right ) x + 3 ^{2} - 6 = 0 \Leftrightarrow x ^{2} - 4 x + 3 = 0[/tex]
[tex]\Delta = \left ( - 2 \right ) ^{2} - 1 . 3 = 1 > 0[/tex]
[tex]\left\{\begin{matrix} x _{1} = \frac{2 - \sqrt{1}}{1} = 1 & & \\ x _{2} = \frac{2 + \sqrt{1}}{1} = 3 & & \end{matrix}\right.[/tex]
b) [tex]\Delta = \left ( m - 1 \right ) ^{2} - \left ( m ^{2} - 6 \right ) = m ^{2} - 2 m + 1 - m ^{2} + 6 = 7 - 2 m[/tex]
Để phương trình có 2 nghiệm [tex]x _{1} ; x _{2}[/tex] thì [tex]\Delta \geq 0[/tex]
[tex]\Rightarrow 7 - 2 m \geq 0 \Rightarrow m \leq \frac{7}{2}[/tex]
Theo viet ta có: [tex]\left\{\begin{matrix} x _{1} + x _{2} = 2 \left ( m - 1 \right ) & & \\ x _{1} x _{2} = m ^{2} - 6 & & \end{matrix}\right.[/tex]
[tex]x _{1}^{2} + x _{2}^{2} = 16 \Leftrightarrow x _{1}^{2} + x _{2}^{2} + 2 x _{1} x _{2} - 2 x _{1} x _{2} = 16[/tex]
[tex]\Leftrightarrow \left ( x _{1} + x _{2} \right ) ^{2} - 2 x _{1} x _{2} = 16 \Leftrightarrow 4 \left ( m - 1 \right ) ^{2} - 2 \left ( m ^{2} - 6 \right ) = 16[/tex]
[tex]\Leftrightarrow 4 m ^{2} - 8 m + 4 - 2 m ^{2} +12 = 16 \Leftrightarrow 2 m ^{2} - 8 m = 0[/tex]
$$\left[ \begin{array}{ll} m = 0 & \\
m=3 &
\end{array} \right.$$
Vậy m nhỏ nhất bằng 0 thì [tex]x _{1}^{2} + x _{2}^{2} = 16[/tex]
Vẫn còn một vài lỗi nhé bạn.$2m^2-8m=0$ thì suy ra $m=0$(nhận) $m=4$(loại do $m \leq \dfrac{7}{2}$. nhé chứ không phải $m=3$.Ở câu a $x^2-4x+3=0$ tới đây để ý hệ số $a+b+c=0$ thì có thể suy ngay ra $x_1=1,x_2=3$ luôn nhé bạn!!.Thân @Nguyễn Xuân Hiếu
Last edited by a moderator:

