giải hế sau

)
y^2 + z^2 =50
x^2 +xy+y^2/2 =169
x^2 +xz+z^2/2 =144
còn nhìu bài hay nhưng hok biết psot kiêủ j cho mọi người hiểu thông cảm@};_
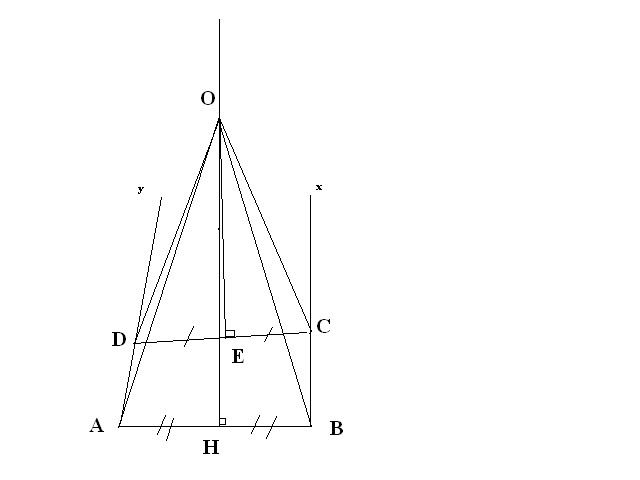
Xét [TEX] A\left( {x;0} \right),B\left( {\frac{{ - y}}{2};\frac{y}{2}} \right);C\left( {\frac{{ - z}}{2};\frac{{ - z}}{2}} \right)[/TEX]
Có [TEX]AB = 13;AC = 12;BC = 5[/TEX] suy ra góc C=90 độ hay ta có
[TEX]vtCA.ctCA = 0[/TEX]
suy ra [TEX]x = \frac{{z^2 }}{{\left( {y - z} \right)}}[/TEX]
Ta thấy rằng C thuộc tia phân giác góc thứ I hoắc III còn B thuộc tia phân giác góc phần tư thứ 2 hoặc 4, ta dễ dàng Cm khi C thuộc góc phần tư thứ I thì B phải thuộc goc phần tư thứ IV ( chứng minh dựa vào việc BC=4<AC=12) Ta xét trường hợp C thuộc góc phần tư thứ I, trường hợp còn lại là nghiệm đối
Hpt tương đương bài toán cho 2 điểm C(c,c) c>0 và B(-b;b) b<0 thỏa mãn BC=5
hãy xác định góc anpha trong đó anpha= giữa BC và đường thẳng y=x sao cho đường vuông góc với Bc kẻ từ C cắt Ox tại A mà AC=12
(mối qun hệ z=-2c,y=2b
ta có mối quan hẹ [TEX]\begin{array}{l}\frac{c}{{c{\rm{os}}\left( {\alpha + 45} \right)}} = 12 \Leftrightarrow \frac{c}{{\frac{1}{{\sqrt 2 }}\left( {c{\rm{os}}\alpha - \sin \alpha } \right)}} = 12, \\ {{\rm t}\nolimits} {\rm{an}}\alpha {\rm{ = }}\frac{{ - b}}{c},b^2 + c^2 = \frac{{25}}{2} \\\end{array}[/TEX]
từ đó suy ra
[TEX]c = - \frac{{12}}{7}b \Leftrightarrow z = \frac{{12}}{7}y[/TEX]
thay vào hệ thức [TEX]z^2 + y^2 = 50,x = \frac{{z^2 }}{{y - z}}[/TEX] với chú ý là z<0,y<0 ta được nghiệm
[TEX]z = - \frac{{60\sqrt 2 }}{{\sqrt {193} }},y = - \frac{{35\sqrt 2 }}{{\sqrt {193} }},x = 144\sqrt {\frac{2}{{193}}} [/TEX]
ngoài ra do giả sử c>0 cho nên ta còn một nghiệm nữa là nghiệm (-x;-y;-z) như trên
là khi con C thuộc góc phần tư thứ 4 và B thuộc góc phân tư thứ III thì con tan anpha quan hệ của nó khác

) nói chung cung làm như trên ra thêm kết quả [tex]x = 144\sqrt {\frac{2}{{433}}} ;y = 85\sqrt {\frac{2}{{433}}} ;z = 60\sqrt {\frac{2}{{433}}} [/tex] đó là đo quan hệ y=17/12z đúng là sơ suất :d
vậy bài toán có 4 nghiệm cộng trừ tưng cái nghiệm kia
C2: x khác 0 đặt
y=ax,z=bx
[TEX]\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} x^2 \left( {a^2 + b^2 } \right) = 50 \\ x^2 \left( {1 + a + \frac{{a^2 }}{2}} \right) = 169 \\ x^2 \left( {1 + b + \frac{{b^2 }}{2}} \right) = 144 \\ \end{array} \right. \\ = > \left\{ \begin{array}{l} \frac{{\left( {a^2 + b^2 } \right)}}{{\left( {1 + a + \frac{{a^2 }}{2}} \right)}} = \frac{{50}}{{169}} \\ \frac{{\left( {a^2 + b^2 } \right)}}{{\left( {1 + b + \frac{{b^2 }}{2}} \right)}} = \frac{{50}}{{144}} \\ \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} 144a^2 - 50a + 169b^2 - 50 = 0 \\119b^2 - 50b + 144a^2 - 50 = 0 \\ \end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l} a = b^2 + b \\ 144b^4 + 288b^3 + 263b^2 - 50b - 50 = 0 \\\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l} a = b^2 + b \\ \left( {12b - 5} \right)\left( {12b + 5} \right)\left( {b^2 + 2b + 2} \right) = 0 \\ \end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l} b = \frac{5}{{12}},a = \frac{{85}}{{144}} \\ b = - \frac{5}{{12}},a = - \frac{{35}}{{144}} \\ \end{array} \right. \\ \Rightarrow \left( {x,y,z} \right) = \left( {144\sqrt {\frac{2}{{193}}} ; - 35\sqrt {\frac{2}{{193}}} ; - 60\sqrt {\frac{2}{{193}}} } \right);\left( { - 144\sqrt {\frac{2}{{193}}} ;35\sqrt {\frac{2}{{193}}} ;60\sqrt {\frac{2}{{193}}} } \right);\left( {144\sqrt {\frac{2}{{443}}} ;85\sqrt {\frac{2}{{443}}} ;60\sqrt {\frac{2}{{433}}} } \right);\left( { - 144\sqrt {\frac{2}{{433}}} ; - 85\sqrt {\frac{2}{{433}}} ; - 60\sqrt {\frac{2}{{433}}} } \right) \\ \end{array}[/TEX]
 )
)