D
duynhan1
Ký hiệu [TEX](0;2)[/TEX] nghĩa là các số nằm giữa 0 và 2 không tính 2 số 0 và 2ANh ơi cho em hỏi [TEX]a,b,c \in [0,1][/TEX] hay [TEX][0,2][/TEX] ạ ! .
Ký hiệu [TEX](0;2)[/TEX] nghĩa là các số nằm giữa 0 và 2 không tính 2 số 0 và 2ANh ơi cho em hỏi [TEX]a,b,c \in [0,1][/TEX] hay [TEX][0,2][/TEX] ạ ! .
Thêm một bài nữa!!
Cho [TEX]a;b;c \in (0;2)[/TEX] thỏa [TEX]a+b+c+abc=4[/TEX]
Chứng minh BDT : [TEX]\sqrt{4-a^2} + \sqrt{4-b^2} + \sqrt{4-c^2} \leq 3\sqrt{3}[/TEX]
bài này hơi khó, mình làm cũng không biết có được không nhưng sách có giải nên lật ra xem, thấy hay post cho mọi người giải thửta có :0\leqa\leq2 \Rightarrow a(a-2)\leq0 \Leftrightarrowa^2 -2a \leq0
0\leqb\leq2\Rightarrow b^2-2b\leq0
0\leqc\leq2\Rightarrowc^2-2c\leq0
chịu c0si chỉ dùng khi \geq0 thôi mà
bài này hơi khó, mình làm cũng không biết có được không nhưng sách có giải nên lật ra xem, thấy hay post cho mọi người giải thử
Em viết lộn dấu rồi kìado [tex]a,b,c \in (0,2)[/tex],[TEX]a-2)(b-2)(c-2) \ge 0[/TEX]
Nói rồi sao ko sửa [TEX](a-1)(b-1)(c-1) \leq 0[/TEX]do [tex]a,b,c \in (0,1)[/tex],[TEX](a-1)(b-1)(c-1) \ge 0[/TEX]
em ko giải theo [tex](a-2)(b-2)(c-2)[/tex] em sửa thành 2 khúc rùi. Theo nguyên lí phân rã. Sách giải thế nào anh !
sai rùi khi z,b,c thuộc khoảng từ 0-->2 thì lun dương rùi dùng cô si lun vẫn đúngta có :0\leqa\leq2 \Rightarrow a(a-2)\leq0 \Leftrightarrowa^2 -2a \leq0
0\leqb\leq2\Rightarrow b^2-2b\leq0
0\leqc\leq2\Rightarrowc^2-2c\leq0
chịu c0si chỉ dùng khi \geq0 thôi mà
ta dễ dàng chứng minh :
[TEX]ab+bc+ca+abc=4[/TEX]
[TEX]\Leftrightarrow \frac{1}{a+2} + \frac{1}{b+2} + \frac{1}{c+2} =1 [/TEX]
Với mọi [TEX]x \in (0;2)[/TEX], theo co si ta có :
[TEX](x+2)^2 (4-x^2) = (x+2)(x+2)(2-x)(2+x) = \frac{1}{3}(x+2)(x+2)(x+2)(6-3x) \leq \frac{1}{3} [\frac{3(x+2) + (6-3x)}{4}]^4=27[/TEX]
Do đó : [TEX]\sqrt{4-x^2} \leq \frac{3\sqrt{3}}{x+2}[/TEX]
Áp dụng cho a,b,c và chú ýta có đpcm
Cho [TEX]a,b,c[/TEX]là các số thực dương thỏa [TEX]abc=1[/TEX]
CM: [TEX](a-1 + \frac{1}{b})(b-1 + \frac{1}{c})(c-1 + \frac{1}{a})\leq1[/TEX]

DÙng AM-GM và Cauchy-Schwarz ta có :bài tiếp đi anh.
Bài khác nè:Cực hay
[TEX]a,b,c>0[/TEX]
Chứng minh:
[TEX]2(\frac{a^2}{b^2}+\frac{b^2}{c^2}+\frac{c^2}{a^2})+3\ge 3(\frac{a}{b}+\frac{b}{c}+\frac{c}{a})[/TEX]
a,b,c không âm và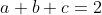
CMR :


