N
nhocngo976
MN // AD, N thuộc SD1 bài hìh học- júp mình nhatks
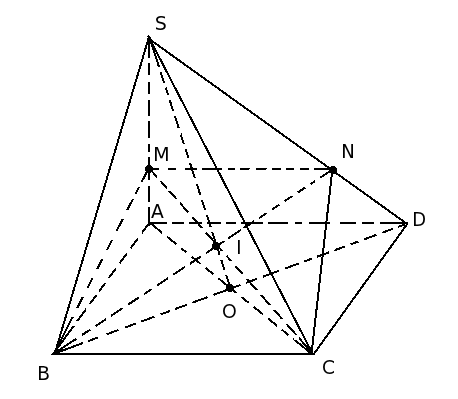
cho hjh chóp S.ABCD có đáy là hinh chữ nhật ABCD vs AB= a,AD=2a,SA vuông góc với đáy, SB tạo với đáy 1 góc 60 độ. Trên cạnh SA lấy điểm M sao cho AM = [TEX]\frac{a\sqrt{3}}{3}[/TEX]. Mặt phẳng (BCM) cắt SD tại N. tính thể tích khối chóp S.BCNM
[TEX]V_{S.BCNM}=V_{S.MBC}+V_{S.MNC}\\\\ \frac{V_{S.MBC}}{V_{S.ABC}}=\frac{SM}{SA}= \frac{2}{3} \\\\ \frac{V_{S.MNC}}{V_{S.ADC}}=\frac{SM.SN}{SA.SD}= \frac{2}{3}.\frac{2}{3}=\frac{4}{9} \\\\ V_{S.ABC}=V_{S.ACD}=\frac{1}{3}.SA.AB.BC=.... \\\\ => V_{S.MBC}+V_{S.MNC}=...[/TEX][TEX][/TEX][TEX][/TEX]