L
V
valdes
Trong không gian cho 4 điểm A(3;1;0) B(1;0;-1) C(3;-2;0) D(0;2;-2). Lập phương trình mặt phẳng phân giác của góc nhị diện ( A; BC; D).
Cho mình hỏi góc nhị diện cần tìm là góc nào vậy?
Cho mình hỏi góc nhị diện cần tìm là góc nào vậy?
Last edited by a moderator:
T
thanhduc20100
Giúp tớ bài này với
((
1) Trong không gian tọa độ cho đường thẳng [TEX]d:\frac{x-3}{2}=\frac{y+2}{1}=\frac{z+1}{-1}[/TEX] và mặt phẳng(P): x+y+z+2=0. Gọi M là giao điểm của d và (P). Viết phương trình đường thẳng [TEX]\Delta [/TEX] nằm trong mặt phẳng (P), vuông góc với d đồng thời thỏa mãn khoảng cách từ M tới [TEX]\Delta [/TEX] bằng [TEX]\sqrt{42}[/TEX]
((1) Trong không gian tọa độ cho đường thẳng [TEX]d:\frac{x-3}{2}=\frac{y+2}{1}=\frac{z+1}{-1}[/TEX] và mặt phẳng(P): x+y+z+2=0. Gọi M là giao điểm của d và (P). Viết phương trình đường thẳng [TEX]\Delta [/TEX] nằm trong mặt phẳng (P), vuông góc với d đồng thời thỏa mãn khoảng cách từ M tới [TEX]\Delta [/TEX] bằng [TEX]\sqrt{42}[/TEX]
S
silvery21
Giúp tớ bài này với
1) Trong không gian tọa độ cho đường thẳng [TEX]d:\frac{x-3}{2}=\frac{y+2}{1}=\frac{z+1}{-1}[/TEX] và mặt phẳng(P): x+y+z+2=0. Gọi M là giao điểm của d và (P). Viết phương trình đường thẳng [TEX]\Delta [/TEX] nằm trong mặt phẳng (P), vuông góc với d đồng thời thỏa mãn khoảng cách từ M tới [TEX]\Delta [/TEX] bằng [TEX]\sqrt{42}[/TEX]
bat vietkey ko dc .co dich nha'
may ma` chieu nay t len mag . toi ko dc len vi` nha` co khach ba me o tren tang cung` t . bai` hinh toa do kia duy nhan giai roi t giai cau nay` thoai nhe'
chu y: t giai thich [TEX]\Delta [/TEX] nam trong (P) nen VTCP cua del ta vuong goc voi VTPT cua (P)
theo gt [TEX]\Delta [/TEX] vuong goc voi(d) nen VTCP cua del ta vuong goc voi VTPT cua (d)
vay VTCP cua [TEX]\Delta [/TEX] = tich co huong cua VTCP cua (P) va` (d) = [2;-3;1]
A(a;b;c) thuoc [TEX]\Delta [/TEX] va A thuoc (P) nen toa do cua (A) thoa man:
a+b+c+2 = 0 (*)
khoảng cách từ M tới [TEX]\Delta [/TEX] bằng [TEX]\sqrt{42}[/TEX] = >
( cai' mau la do dai cua vec to nhe')
ket hop (*) voi (*)(*) cau chon duoc a; b ;c .. tu do c viet dc pt delta roi ( co VTCP ; va` di qua A) tu giai tip nha
Last edited by a moderator:
C
connguoivietnam
[TEX]M(1;-3;0)[/TEX]
[TEX]u_{ \Delta}[/TEX] là sự tổng hợp tích có hướng của [TEX]u_d[/TEX] và [TEX]n_{(P)}[/TEX]
có véctơ chỉ phương của đ/t [TEX]\Delta[/TEX] kẻ MH vuông góc với đ/t [TEX]\Delta[/TEX]
tại H gọi [TEX]H(x_H;y_H;z_H)[/TEX]
phương trình thứ nhất là H thuộc mặt phẳng (P)
phương trình thứ 2 là véctơ [TEX]MH.u_{ \Delta}=0[/TEX] (tích vô hướng)
phương trình thứ 3 là [TEX]|MH|=\sqrt{42}[/TEX]
giải ra [TEX]H[/TEX] có [TEX]u_{ \Delta}[/TEX] rồi lập p/t thôi
[TEX]u_{ \Delta}[/TEX] là sự tổng hợp tích có hướng của [TEX]u_d[/TEX] và [TEX]n_{(P)}[/TEX]
có véctơ chỉ phương của đ/t [TEX]\Delta[/TEX] kẻ MH vuông góc với đ/t [TEX]\Delta[/TEX]
tại H gọi [TEX]H(x_H;y_H;z_H)[/TEX]
phương trình thứ nhất là H thuộc mặt phẳng (P)
phương trình thứ 2 là véctơ [TEX]MH.u_{ \Delta}=0[/TEX] (tích vô hướng)
phương trình thứ 3 là [TEX]|MH|=\sqrt{42}[/TEX]
giải ra [TEX]H[/TEX] có [TEX]u_{ \Delta}[/TEX] rồi lập p/t thôi
T
thanhduc20100
1) Cho đường thẳng (D) có pt;[TEX]\left\{x=-2+t\\\ y=-2t\\\ z=2+2t[/TEX]. Gọi[TEX]\Delta [/TEX] là đường thẳng qua điểm A(4;0;-1) song song với (D) và I(-2;0;2) là hình chiếu vuông góc của A trên (D). Trong các mặt phẳng qua[TEX]\Delta [/TEX], hãy viết phương trình của mặt phẳng có khoảng cách đến (D) là lớn nhất
2) trong không gian với hệ tọa độ Oxyz cho 2 đường thẳng d và d' lần lượt có phương trình:
[TEX]d:\frac{x}{1}=\frac{y-2}{-1}=\frac{z}{1}[/TEX] và [TEX]d':\frac{x-2}{2}=y-3=\frac{z+5}{-1}[/TEX]. viết pt mặt phẳng [TEX](\alpha )[/TEX] đi qua d và tạo với d' 1 góc 30*.
2) trong không gian với hệ tọa độ Oxyz cho 2 đường thẳng d và d' lần lượt có phương trình:
[TEX]d:\frac{x}{1}=\frac{y-2}{-1}=\frac{z}{1}[/TEX] và [TEX]d':\frac{x-2}{2}=y-3=\frac{z+5}{-1}[/TEX]. viết pt mặt phẳng [TEX](\alpha )[/TEX] đi qua d và tạo với d' 1 góc 30*.
A
acsimet_91
Đề bài này có vẻ đơ đơ nhỉ?
Gọi [TEX](P)[/TEX] là qua [TEX](\Delta)[/TEX]
Do [TEX](P)[/TEX] đi qua [TEX]\Delta[/TEX] \Rightarrow [TEX]D[/TEX] chứa A
Do [TEX](\Delta) // (D) \Rightarrow (D)//(P)[/TEX]
Gọi [TEX]B[/TEX] là hình chiếu của I lên (P)
\Rightarrow khoảng cách giữa [TEX](D)[/TEX] vs [TEX](P)[/TEX] = [TEX]BI[/TEX]
Tam giác BIA vuông tại B \Rightarrow [TEX]BI \leq AI[/TEX]
Vậy khoảng cách [TEX]((P).(D))[/TEX] max \Leftrightarrow IA vuông góc với vs (P)
Mặt khác [TEX](P)[/TEX] đi qua A \Rightarrow pt (P)
Gọi [TEX]u(a,b,c)[/TEX] là VTPT.
(d'): VTCP: [TEX]u_1 ( 2,1,-1)[/TEX]
(d): VTCP: [TEX]u_2 (1,-1,1)[/TEX]
(P) t/m db \Leftrightarrow [TEX]cos (u,u_1)=\frac{1}{2}[/TEX] hoặc [TEX]cos(u,u_1)=\frac{-1}{2}[/TEX]
lai co': [TEX]u.u_2=0[/TEX]
Từ đó suy ra hệ 2 pt 3 ẩn a,b, c
Chọn c=1 \Rightarrow a,b \Rightarrow [TEX]u[/TEX]
lấy bừa 1 điểm trên (d) rồi cho [TEX](\anpha)[/TEX] đi qua điểm đó, nhận [TEX]u[/TEX] làm VTPT
Tự tính đi em =))
T
thanhduc20100
Bài 1: Công nhận đề sao ấy nhỉ, không cần tính vecto chỉ phương của [TEX]\Delta [/TEX], chỉ cần tính AI và đi qua A thế là xong, chẳng biết nó dễ hay là có vấn đề gì nữa((
P/s: Anh rễ nhác quá)
((P/s: Anh rễ nhác quá
)
A
ang3l_l0v3_teen9x
Giúp mình giải bài này nhé, thanks!
Cho tam giác đều ABC. Trên đường thẳng d vuông góc với mặt phẳng (ABC) tại A, lấy một điểm M. Gọi H và O lần lượt là trực tâm của các tam giác ABC và MBC.
a, Chứng minh MC vuông góc với mặt phẳng (BOH) và OH vuông góc mặt phẳng (BCM)
b, Đường thẳng OH cắt d tại N, chứng minh tứ diện BCMN có các cặp cạnh đối diện đôi một vuông góc với nhau
__________________
Xin lỗi vì mình đã post bài trùng lặp , vì chưa hiểu bài này nên mình post lại mong mọi người chỉ giúp!
Cho tam giác đều ABC. Trên đường thẳng d vuông góc với mặt phẳng (ABC) tại A, lấy một điểm M. Gọi H và O lần lượt là trực tâm của các tam giác ABC và MBC.
a, Chứng minh MC vuông góc với mặt phẳng (BOH) và OH vuông góc mặt phẳng (BCM)
b, Đường thẳng OH cắt d tại N, chứng minh tứ diện BCMN có các cặp cạnh đối diện đôi một vuông góc với nhau
__________________
Xin lỗi vì mình đã post bài trùng lặp , vì chưa hiểu bài này nên mình post lại mong mọi người chỉ giúp!
N
nhocngo976
a,
[TEX]\left{BH \bot AC \\ BH \bot d \right. ------> BH \bot (MAC)---> BH \bit MC (1) \\\\ O truc \ tam \ \Delta MBC ---> BO \bot MC (2) \\\\\ (1)(2)=> MC \bot (BOH) [/TEX]
[TEX]OH \bot MC ( \ do \ OH \ thuoc \ (BOH)) \ (3)\\\\ AH \cap BC=A1 [/tex]
do ABC đều, ---> AB=AC mà AB,AC là hình chiếu của MB,MC ---> MB=MC ----> MO cắt BC cũng tại A1
[tex]\\\\ \left{\begin{ AM \bot BC \\ AA1 \bot BC \right. ----> (AMA1) \bot BC \ ma \ OH \ thuoc \ (AMA1) ----> OH \bot BC \ (4) \ \\\\ (3)(4) ---> OH \bot (MBC) [/TEX]
T
trantoan0593
N
ngomaithuy93
Cho mặt cầu [TEX](S): x^2+y^2+z^2+2x-2y+2z-1=0[/TEX]
A(3;1;0), B(2;0;-2)
Viết pt mp (P) đi qua A, B sao cho thiết diện của (P) với mặt cầu (S) là đtròn có diện tích =pi =((
A(3;1;0), B(2;0;-2)
Viết pt mp (P) đi qua A, B sao cho thiết diện của (P) với mặt cầu (S) là đtròn có diện tích =pi =((
H
hung11493
a, BH vuông vs MC (BH vuông ACM)
BO vuông MC ( đường cao ) => MC vuông góc (BHO)
OH vuông BC ( OH thuộc (AHM) vuông BC )
MC vuông OH ( MC vuông vs (OBH) ) => OH vuông góc (MBC)
b, cm MN vs BC MN thuộc d vuông góc ABC nên MN vuông BC
BN vs CM do M thuộc OH nên M thuộc BOH mà MC vuông vs BOH ( câu a ) nên MC vuông BN
BM vs CN do OH vuông góc BM (cm cau a), va` CO vuông góc BM =>BM vuông góc mpCOH, mà CN thuộc COH nên CN vuông góc với BM
L
linh030294
(*) Câu 1 : Cho hình chóp tam giác đều ABC , cạnh đáy a , góc giữa hai cạnh bên và đáy là 60 độ . M là trung điểm SA . Tính thể tích CBSM .
---> Lưu ý : Sử dụng phương pháp toạ độ hoá
---> Lưu ý : Sử dụng phương pháp toạ độ hoá
N
nhoc_maruko9x
Spam phát chứ bài này mà dùng toạ độ hoá đúng là sai lầm.. Đặt Ox Oy thì thôi rồi, mà điểm M tìm toạ độ thì cứ gọi là :khi (69):(*) Câu 1 : Cho hình chóp tam giác đều ABC , cạnh đáy a , góc giữa hai cạnh bên và đáy là 60 độ . M là trung điểm SA . Tính thể tích CBSM .
---> Lưu ý : Sử dụng phương pháp toạ độ hoá
Xin giải theo cách bình dân, không chơi sang vậy...
Dễ thấy SO (O là tâm ABC) = a, nên [tex]V_{SABC} = \fr13SO.S_{ABC} = \fr{a^3\sqr{3}}{12}[/tex]
[tex]\fr{V_{SMBC}}{V_{SABC}} = \fr{SM}{SA}.\fr{SB}{SB}.\fr{SC}{SC} = \fr12 \Rightarrow V_{SMBC} = \fr{a^3\sqr{3}}{24}[/tex]
Last edited by a moderator:
K
kiburkid
Cho hình chóp S.ABC, tam giác ABC vuông tại C, AC=2, BC=4, SA=5, SA vuông góc với (ABCD), D là trung điểm của AB
a, Tính góc giữa SD và AC
b, Tính khoàng cách giữa BC và SD
a, Tính góc giữa SD và AC
b, Tính khoàng cách giữa BC và SD
N
nhoc_maruko9x
Bài này lắp trục vào được rồi đây:
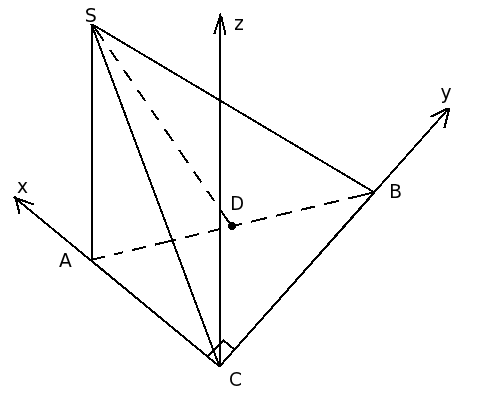
Dễ dàng tìm được [tex]\left\{A(2;0;0)\\B(0;4;0)\\S(2;0;5)\\D(1;2;0)[/tex]
[tex]\Rightarrow \left\{\vec{SD} = (-1;0;-5)\\\vec{AC}=(-2;0;0)\\\vec{BC}=(0;-4;0)[/tex]
[tex]\Rightarrow \left\{cos(AC,SD)=\fr{|\vec{AC}.\vec{SD}|}{|\vec{AC}|.|\vec{SD}|}=\fr{1}{\sqr{26}}\\d(BC,SD) =\fr{|[\vec{BC},\vec{SD}].\vec{SC}|}{|[\vec{BC},\vec{SD}]|} = \fr{5}{\sqr{26}}[/tex]
Số lẻ ghê, nhìn cái đống vector kia chắc loạn chỗ nào rồi.
K
kiburkid
N
nhocngo976
a, kẻ DE // AC (E thuộc BC) ---> E trung điểm BC
[TEX]SD^2=SA^2+AD^2=5^2+ \frac{2^2+4^2}{4}=30 \\\\ \left{ BC \bot AC \\ BC \bot SA \right. ----> BC \bot SC \\\\ SC^2=SA^2+AC^2=29 \\\\ SE^2= SC^2+EC^2= 33 \\\\ DE =\frac{1}{2}AC=1 \\\\ cos \widehat{SDE}= \frac{SD^2+DE^2-SE^2}{2.SD.SE}= \frac{-1}{\sqrt{30}} ---> \widehat{SDE} >90 \\\\ ---> \widehat{SD;AC}=180- \widehat{SDE}=... [/TEX]
b, gọi F trung điểm AC , ta có:
[TEX]DF \bot AC ----> SF \ hinh \ chieu \ cua \ AD \ len \ (SAC) [/TEX]
[TEX]ke \ CK \bot SF \ , KJ // DF ( J \in SD) , \ JN // CK (N \in BC) ----> JN \ la \ duong \ vuong \ goc \ chung ----> d(SD;BC)= JN=CK \\\\ SF^2= \frac{SA^2+SC^2}{2}-\frac{AC^2}{4} = 26 \\\\ \Delta SAF \ dong \ dang \ \Delta CKF ---> \frac{CK}{SA}= \frac{CF}{SF} ----> CK=\frac{CF.SF}{SA}=\frac{\sqrt{26}}{5}[/TEX][TEX][/TEX]
N
narcissus234
1 bài hìh học- júp mình nha tks
cho hjh chóp S.ABCD có đáy là hinh chữ nhật ABCD vs AB= a,AD=2a,SA vuông góc với đáy, SB tạo với đáy 1 góc 60 độ. Trên cạnh SA lấy điểm M sao cho AM = [TEX]\frac{a\sqrt{3}}{3}[/TEX]. Mặt phẳng (BCM) cắt SD tại N. tính thể tích khối chóp S.BCNM
tkscho hjh chóp S.ABCD có đáy là hinh chữ nhật ABCD vs AB= a,AD=2a,SA vuông góc với đáy, SB tạo với đáy 1 góc 60 độ. Trên cạnh SA lấy điểm M sao cho AM = [TEX]\frac{a\sqrt{3}}{3}[/TEX]. Mặt phẳng (BCM) cắt SD tại N. tính thể tích khối chóp S.BCNM