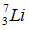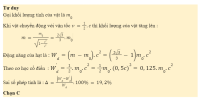Câu 1: Ta có:
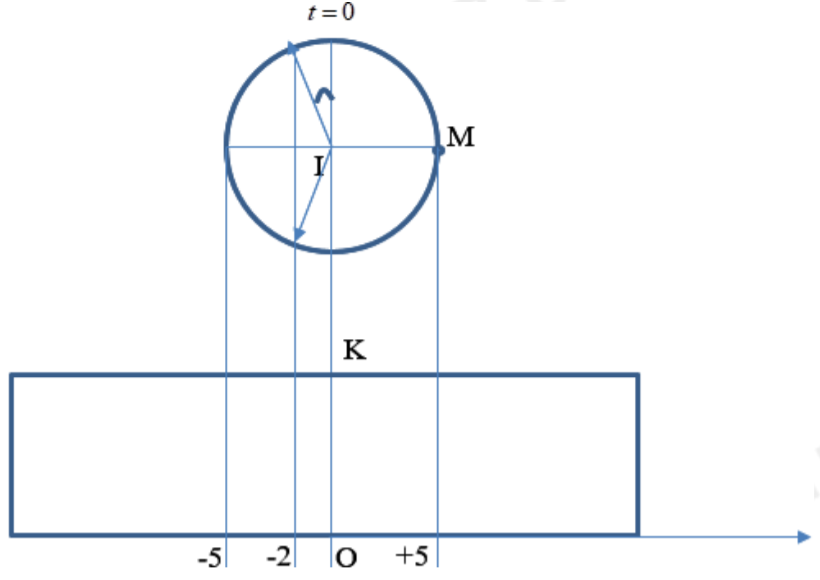
Chu kì dao động: $T=\frac{1}{f}=0,2s$
Gọi $M_1, M_2$ lần lượt là hình chiếu của M trên mặt nước và trên đáy bể.
Ta có: $M_1$ và $M_2$ đều dao động điều hòa với phương trình: $x=5cos(10\pi t-\frac{\pi}{2})cm$ (do tại thời điểm ban đầu M ở điểm cao nhất)
Khoảng thời gian ánh sáng truyền từ điểm M đến đáy bể:
Trong 1 chu kì, điểm sáng dưới đáy bể qua vị trí x=-2cm 2 lần
$\Rightarrow t_{2020}=\frac{2020}{2}T =202s$
Mặt khác $t_1=\frac{\Delta \varphi}{\omega}$
Lại có: $cos\Delta \varphi=|\frac{-2}{5}|=\frac{2}{5} \Rightarrow \Delta \varphi=1,159rad$
$\Rightarrow t_1=\frac{\Delta \varphi}{\omega}=0,0369s \Rightarrow t=t_{2020}+t_1=202,036s$
Câu 2:
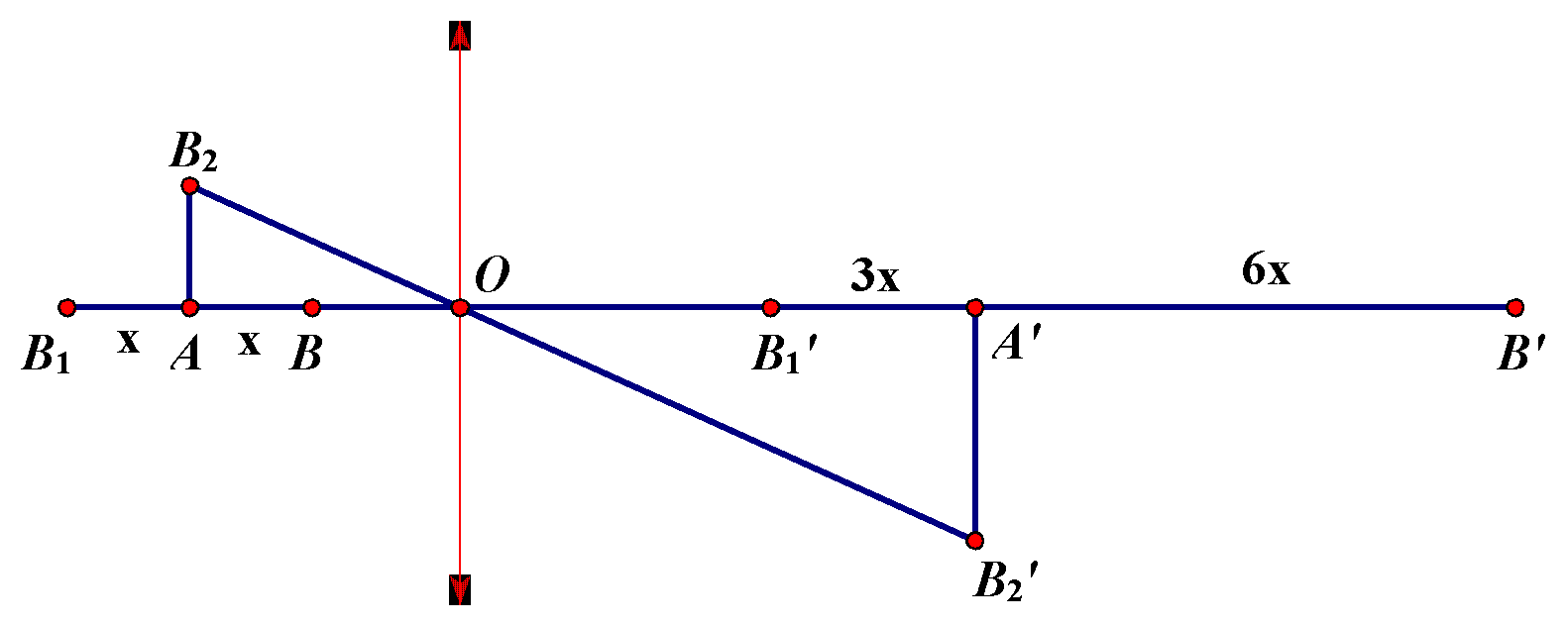
Đặt $AB = x; OA = a; OA’ = a’; OB = b; OB’ = b’; OB_1 = b_1; OB_1’ = b_1’.$
Công thức của thấu kính hội tụ:
[tex]\left\{\begin{matrix} \frac{1}{a}+\frac{1}{a'}=\frac{1}{f} \\ \frac{1}{b}+\frac{1}{b'}=\frac{1}{f} \\ \frac{1}{b_1}+\frac{1}{b_1'}=\frac{1}{f} \end{matrix}\right.[/tex] [tex]\Leftrightarrow \left\{\begin{matrix} \frac{1}{a}+\frac{1}{a'}=\frac{1}{b}+\frac{1}{b'} \\ \frac{1}{a}+\frac{1}{a'}=\frac{1}{b_1}+\frac{1}{b_1'} \end{matrix}\right.[/tex] [tex]\Leftrightarrow \left\{\begin{matrix} \frac{a-b}{ab}=\frac{b'-a'}{a'b'} \\ \frac{b_1-a}{ab_1}=\frac{a'-b_1'}{a'b_1'} \end{matrix}\right.[/tex] [tex]\Leftrightarrow \left\{\begin{matrix} \frac{x}{ab}=\frac{6x}{a'b'} \\ \frac{x}{ab_1}=\frac{3x}{a'b_1'} \end{matrix}\right.[/tex] [tex]\Leftrightarrow \frac{a}{a'}=\frac{b'}{6b}=\frac{b_1'}{3b_1}[/tex]
Chú ý rằng $b + b_1 = 2a$ và $2b_1’ + b’ = 3a’$. Áp dụng tính chất dãy tỉ số bằng nhau:
[tex]\frac{a}{a'}=\frac{b'}{6b}=\frac{b_1'}{3b_1}=\frac{2b_1'}{6b_1}=\frac{b'+2b_1'}{6b+6b_1}=\frac{3a'}{12a}=\frac{a'}{4a}\Rightarrow \frac{a}{a'}=\frac{1}{2}[/tex]
Suy ra [tex]\frac{A'B_2'}{AB_2}=\frac{a'}{a}=2[/tex]
Vì ảnh ngược chiều với vật nên số phóng đại ảnh là – 2.
Câu 3:
Điều kiện trùng ba: [tex]x_{\equiv 3}=k_1i_1=k_2i_2=k_3i_3 (k_1;k_2;k_3\in Z)\Leftrightarrow k_1\lambda_1=k_2\lambda_2=k_3\lambda_3[/tex]
[tex]\Leftrightarrow 0,42k_1=0,56k_2=\lambda_3k_3\Leftrightarrow 3k_1=4k_2=...k_3[/tex]
Các cặp trùng nhau của bức xạ 1 và 2 là: (0,0);(4,3);(8,6);(12,9);...
(0,0) là cặp vân trung tâm trùng ba, trong khoảng hai vân sáng cùng màu vân trung tâm (vân trùng ba) có 2 vân trùng màu 1 và 2 nên cặp (12,9) là cặp trùng ba tiếp theo.
Giữa cặp (0,0,0) và (12,9,c) có 3 vân trùng đôi của 1 và 3 nên cặp trùng đôi đầu tiên của 1 và 3 là (3,k) [tex]\Rightarrow 3i_1=ki_3\Leftrightarrow 3\lambda_1=k\lambda_3\Rightarrow k=\frac{3\lambda_1}{\lambda_3}=\frac{3.0,42}{\lambda_3}(*)[/tex]
Thay 4 đáp án đề cho vào (*), thấy với $\lambda_3=0,63\mu m$ thì $k=2 \in Z$ thỏa mãn.
Chu kì dao động: $T=\frac{1}{f}=0,2s$
Gọi $M_1, M_2$ lần lượt là hình chiếu của M trên mặt nước và trên đáy bể.
Ta có: $M_1$ và $M_2$ đều dao động điều hòa với phương trình: $x=5cos(10\pi t-\frac{\pi}{2})cm$ (do tại thời điểm ban đầu M ở điểm cao nhất)
Khoảng thời gian ánh sáng truyền từ điểm M đến đáy bể:
Trong 1 chu kì, điểm sáng dưới đáy bể qua vị trí x=-2cm 2 lần
$\Rightarrow t_{2020}=\frac{2020}{2}T =202s$
Mặt khác $t_1=\frac{\Delta \varphi}{\omega}$
Lại có: $cos\Delta \varphi=|\frac{-2}{5}|=\frac{2}{5} \Rightarrow \Delta \varphi=1,159rad$
$\Rightarrow t_1=\frac{\Delta \varphi}{\omega}=0,0369s \Rightarrow t=t_{2020}+t_1=202,036s$
Câu 2:
Đặt $AB = x; OA = a; OA’ = a’; OB = b; OB’ = b’; OB_1 = b_1; OB_1’ = b_1’.$
Công thức của thấu kính hội tụ:
[tex]\left\{\begin{matrix} \frac{1}{a}+\frac{1}{a'}=\frac{1}{f} \\ \frac{1}{b}+\frac{1}{b'}=\frac{1}{f} \\ \frac{1}{b_1}+\frac{1}{b_1'}=\frac{1}{f} \end{matrix}\right.[/tex] [tex]\Leftrightarrow \left\{\begin{matrix} \frac{1}{a}+\frac{1}{a'}=\frac{1}{b}+\frac{1}{b'} \\ \frac{1}{a}+\frac{1}{a'}=\frac{1}{b_1}+\frac{1}{b_1'} \end{matrix}\right.[/tex] [tex]\Leftrightarrow \left\{\begin{matrix} \frac{a-b}{ab}=\frac{b'-a'}{a'b'} \\ \frac{b_1-a}{ab_1}=\frac{a'-b_1'}{a'b_1'} \end{matrix}\right.[/tex] [tex]\Leftrightarrow \left\{\begin{matrix} \frac{x}{ab}=\frac{6x}{a'b'} \\ \frac{x}{ab_1}=\frac{3x}{a'b_1'} \end{matrix}\right.[/tex] [tex]\Leftrightarrow \frac{a}{a'}=\frac{b'}{6b}=\frac{b_1'}{3b_1}[/tex]
Chú ý rằng $b + b_1 = 2a$ và $2b_1’ + b’ = 3a’$. Áp dụng tính chất dãy tỉ số bằng nhau:
[tex]\frac{a}{a'}=\frac{b'}{6b}=\frac{b_1'}{3b_1}=\frac{2b_1'}{6b_1}=\frac{b'+2b_1'}{6b+6b_1}=\frac{3a'}{12a}=\frac{a'}{4a}\Rightarrow \frac{a}{a'}=\frac{1}{2}[/tex]
Suy ra [tex]\frac{A'B_2'}{AB_2}=\frac{a'}{a}=2[/tex]
Vì ảnh ngược chiều với vật nên số phóng đại ảnh là – 2.
Câu 3:
Điều kiện trùng ba: [tex]x_{\equiv 3}=k_1i_1=k_2i_2=k_3i_3 (k_1;k_2;k_3\in Z)\Leftrightarrow k_1\lambda_1=k_2\lambda_2=k_3\lambda_3[/tex]
[tex]\Leftrightarrow 0,42k_1=0,56k_2=\lambda_3k_3\Leftrightarrow 3k_1=4k_2=...k_3[/tex]
Các cặp trùng nhau của bức xạ 1 và 2 là: (0,0);(4,3);(8,6);(12,9);...
(0,0) là cặp vân trung tâm trùng ba, trong khoảng hai vân sáng cùng màu vân trung tâm (vân trùng ba) có 2 vân trùng màu 1 và 2 nên cặp (12,9) là cặp trùng ba tiếp theo.
Giữa cặp (0,0,0) và (12,9,c) có 3 vân trùng đôi của 1 và 3 nên cặp trùng đôi đầu tiên của 1 và 3 là (3,k) [tex]\Rightarrow 3i_1=ki_3\Leftrightarrow 3\lambda_1=k\lambda_3\Rightarrow k=\frac{3\lambda_1}{\lambda_3}=\frac{3.0,42}{\lambda_3}(*)[/tex]
Thay 4 đáp án đề cho vào (*), thấy với $\lambda_3=0,63\mu m$ thì $k=2 \in Z$ thỏa mãn.
Bài tập nâng cao hạt nhân nguyên tử
A. $147^0$.
B. $148^0$.
C. $150^0$.
D. $120^0$.
Câu 2: Tiêm vào máu bệnh nhân $10 cm^3$ dung dịch chứa [tex]^{24}Na[/tex] có chu kì bán rã 15 giờ với nồng độ $10^{–3}$ mol/lít. Sau 6 giờ lấy $10 cm^3$ máu tìm thấy $1,4.10^{–8}$ mol $^{24}Na$. Coi $^{24}Na$ phân bố đều trong máu của bệnh nhân. Lượng máu của bệnh nhân này vào khoảng
A. 4,8 lít.
B. 5,1 lít.
C. 5,4 lít.
D. 5,6 lít
Câu 3: Giả sử có một hỗn hợp gồm hai chất phóng xạ có chu kì bán rã là $T_1$ và $T_2$, với $T_2 = 2T_1$. Ban đầu t = 0, mỗi chất chiếm 50% về số hạt. Đến thời điểm t, tổng số hạt nhân phóng xạ của khối chất giảm xuống còn một nửa so với ban đầu. Giá trị của t là
A. $0,91T_2. $
B. $0,49T_2. $
C. $0,81T_2. $
D. $0,69T_2.$