G
- Status
B
bigbang195
B
bigbang195
H
herrycuong_boy94
ta luôn có
( cái này chứng minh dễ dàng
)áp dụng BDT
==>
===> đây là tam giác đều
)==> nghiệm chẵn
)Bigbang làm rồi mà /
Last edited by a moderator:
G
gaconthaiphien
Giải phương trình:
[TEX]\frac{\sqrt{1 - sin2x} + \sqrt{1 + sin2x}}{sinx} = 4cosx[/TEX]
Con này em chuyển [TEX]\sqrt{1 - sin2x} = sinx - cosx [/TEX] thì có phải để trị tuyệt đối để giải ko ạ ? Nếu để trị tuyệt đối giải thì phải bìng phương 2 vế ạ ?
[TEX]\frac{\sqrt{1 - sin2x} + \sqrt{1 + sin2x}}{sinx} = 4cosx[/TEX]
Con này em chuyển [TEX]\sqrt{1 - sin2x} = sinx - cosx [/TEX] thì có phải để trị tuyệt đối để giải ko ạ ? Nếu để trị tuyệt đối giải thì phải bìng phương 2 vế ạ ?
D
duykien94
Giải bài này trước (Dễ nhất)
[TEX]3. cos^{13}{x} + sin^{14}{x} = 1[/TEX] (1)
Ta có:
[TEX]|Cosx| \leq 1 \Rightarrow Cos^{13}x \leq Cos^2x \\ Sin^2x \leq 1 \Rightarrow Sin^{14}x \leq Sin^2x[/TEX]
Do đó pt (1) thỏa khi
[TEX]\left[\begin{Cosx = 1}\\{Sin^2x = 1} [/TEX]
\Leftrightarrow [TEX]\left[\begin{x = k2\pi}\\{x = \pi/2 + l\pi} [/TEX] (k, l [TEX]\in[/TEX] Z)
Ta CMR ngoài hai họ nghiệm này, (1) ko còn có nghiệm nào khác;
Thật vậy. Giả sử (1) có nghiệm: [TEX]x_o \neq k2\pi[/TEX] và [TEX]x_o \neq \pi/2 + l\pi[/TEX]
Suy ra:
[TEX]Cos^{13}x_o < Cos^2x_o \\ Sin^{14}x_o < Sin^2x_o[/TEX]
Do đó [TEX]Cos^{13}x_o + Sin^{14}x_o < 1.[/TEX] Vô lý
Vậy pt đã cho có 2 họ nghiệm là ...
Xong rồi
Hix, topic này có 65 trang rồi à. Mình ko để ý lại làm bài từ trang đầu tiên. Sr các bạn =.=
Last edited by a moderator:
M
minhkhac_94
ta luôn có
( cái này chứng minh dễ dàng
_______________________cm đi cậu___________________
D
duynhan1
[TEX]tan A = - tan (B+C)= \frac{tan B + tan C}{tan B. tan C- 1} = \frac{cot B + cot C}{1 - cot B . cot C}[/TEX] (chia tử mẫu cho [TEX]tan B.tanC[/TEX])
[TEX]\Leftrightarrow cot A . cot B + cot B . cot C + cot C . cot A = 1[/TEX]
M
minhkhac_94
Cũng ko phải là dễ dàng chứ
Xét thiểu các trường hợp rồi duynhan
- Cái đẳng thức của cậu chỉ đúng khi cosA,cosB,cosC khác 0
- Cái đẳng thức đã cho đúng với mọi A,B,C
cosA or cosB or cos C =0 BDT hiển nhiên đúng.
Quên xét
Last edited by a moderator:
N
nhocngo976
sr sửa đề tí nha, làm rùi mới nhìn lại đề, haiz, chắc bài kia bn làm tương tự vậy...
[TEX]\frac{\sqrt{1 - sinx} + \sqrt{1 + sinx}}{sinx} = 4cosx[/TEX]
cái này hơi dài nè
ĐK [TEX]\left\{\begin{1+cosx \neq 0}\\{1-cosx\neq 0}(*)\\{cosx \neq 0}[/TEX]
\Leftrightarrow[TEX]\sqrt{1 -sinx} + \sqrt{1 +sinx}= 4cosxsinx[/TEX]
\Leftrightarrow[TEX]\left\{\begin{sinxcos \geq 0}(*)\\2 +2\sqrt{1 -sin^2x} = 16sin^2xcos^2x[/TEX]
\Leftrightarrow[TEX]1 +\|cosx|\ = 8(1 -cos^2x)cos^2x[/TEX]
\Leftrightarrow[TEX]8cos^4x -8cos^2x +\|cosx|\ +1 =0[/TEX]
đặt[TEX]\| cosx |\ =t \\t \in [0; 1](***)[/TEX]
\Rightarrow pt đv t [TEX]8t^4 -8t^2 +t +1 =0[/TEX]
\Leftrightarrow[TEX](t +1)( 2t -1)(4t^2 -2t -1)=0[/TEX]
\Leftrightarrow[TEX]\left[\begin{t =-1}\\{t = \frac{1}{2}}\\{t =\frac{1+\sqrt{5}}{4}}\\{t=\frac{1 -\sqrt{5}}{4}}[/TEX]
kết hợp (***)
\Leftrightarrow[TEX]\left[\begin{t =\frac{1}{2}\\{ t=\frac{1 +\sqrt{5}}{4}[/TEX]
Với [TEX]t = \frac{1}{2}[/TEX] \Leftrightarrow[TEX]\left[\begin{x =\frac{\pi}{3} +k2\pi}\\{x = \frac{-\pi}{3} +k2\pi}\\{x=\frac{2\pi}{3}+k2\pi}\\{x=\frac{-2\pi}{3}+k2\pi}[/TEX]
kết hợp (**) \Rightarrow[TEX]\left[\begin{x=\frac{\pi}{3} +k2\pi}\\{x=\frac{-2\pi}{3} +k2\pi}[/TEX]
với [TEX]t=\frac{1+\sqrt{5}}{4}[/TEX]...(nhìu gê)
dc nghiệm kết hợp (**) dc 2 nghiệm nũa (cái này bn tự làm đi nha, viết bằng text rắc rối quá)
kết hợp (*) \Rightarrownghiệm...
Last edited by a moderator:
H
herrycuong_boy94
Cách khác : từ đẳng thức quen thuộc
( cũng như nhau thôi phải không Duynhan1 ?? )
)
Last edited by a moderator:
B
bigbang195
D
duynhan1
[TEX](gt) \Leftrightarrow \left{ cosx + cos y + cos z = 0 \\ cos^3 x + cos^3 y + cos^3 z = 0 [/TEX]
[TEX]\Leftrightarrow \left{ cos x + cos y + cos z= 0 \\ 3(cos x + cos y)(cos y + cos z )( cos z + cos x) = 0[/TEX]
Không mất tính tổng quát giả sử : [TEX]\left{ cos x + cos y = 0 \\ cos z = 0 [/TEX]
[TEX]\Leftrightarrow \left{ cos x =- cos y \\ cos z = 0 [/TEX]
[TEX]\Rightarrow cos 2x . cos 2y . cos 2z = (1- 2cos^2 x)^2 . ( 1- 2.0^2) [/TEX]
Mà [TEX]{-1 \le 1- 2 cos^2 x \le 1 [/TEX]
[TEX]\Leftrightarrow (1- 2cos^2 x)^2 \le 1 [/TEX]
KL : [TEX]Max \ \ cos 2x. cos 2y . cos2z = 1 \Leftrightarrow (cos x; cos y; cos z) = \left[ (0;0;0) \\ (0;1;-1)[/TEX] và các hoán vị
B
bigbang195
M
minhkhac_94
B
bigbang195
M
minhkhac_94
H
herrycuong_boy94
cần gì phải phức tạp hoá thế, cứ áp dụng phương trình lượng giác cơ bản đi mà
>->-thế thôi là xong
cái này chắc không cần xét điều kiện đâu nhỉ
)
Last edited by a moderator:
M
minhkhac_94
cần gì phải phức tạp hoá thế, cứ áp dụng phương trình lượng giác cơ bản đi mà
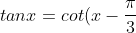\\%20%3C=%3E%20cot(\frac{\pi%20}{2}-x)=cot(x-\frac{\pi}{3})\\%20%3C=%3E%20\frac{\pi%20}{2}-x=x-%20\frac{\pi%20}{3}+k\pi%20\\%20%3C=%3Ex=%20\frac{5\pi%20}{12}+k\pi)
thế thôi là xong
cái này chắc không cần xét điều kiện đâu nhỉ
vẫn phải ĐK như thường vì nó ko phải pt cơ bản ________
B
bigbang195
Last edited by a moderator:
- Status