T
trydan
1)tìm giá trị nhỏ nhất của :
[TEX]A = \frac{(x+y+1)^2}{xy+x+y} + \frac{xy+x+y}{(x+y+1)^2}[/TEX](với x,y là các số thực dương )
Cái này điểm rơi!
1)tìm giá trị nhỏ nhất của :
[TEX]A = \frac{(x+y+1)^2}{xy+x+y} + \frac{xy+x+y}{(x+y+1)^2}[/TEX](với x,y là các số thực dương )
Bài 1: Hiển nhiên: [tex](a+b)(a-b)^2 \ge 0 \to a^3+b^3 \ge ab(a+b)[/tex]trên là cái hới khó còn đây là cái dễ hơn!
1/ Cho [tex]a, b, c>0[/tex], CMR: [tex]a^3+b^3+c^3 \geq a^2\sqrt{bc}+b^2\sqrt{ca}+c^2\sqrt{ab}[/tex].
2/ Cho a, b, c là các số dương thoả [tex]ab+bc+ca=3[/tex], CMR:
a/ [tex]a^3+b^3+c^3 \geq 3[/tex]
b/ [tex]\frac{a}{2a^2+bc}+ \frac{b}{2b^2+ca}+ \frac{c}{2c^2+ab} \geq abc[/tex].
ko phải đâu bạn mà mình làm ngượ lại rồi ghi ra cho no hay thôi!Bạn bboy114crew này Nếu chỉ là mò điểm rơi thôi thì làm sao bạn chọn được
(a+b)(a-b)^2[TEX]\geq[/TEX]0 vậy
Mình có 1 bài BĐT này:
[TEX]Cho x, y> 0 [/TEX]thoả[TEX]x+ y =1.[/TEX] Tìm [TEX]minM= (x^2 + \frac{1}{y^2}) (y^2 + \frac{1}{x^2})[/TEX]
Mình sửa bài rồi đó, các bạn làm đi nha!
[TEX]\huge \blue \Leftrightarrow M=x^2y^2+\frac{1}{x^2y^2}+2=x^2y^2+\frac{1}{256x^2y^2}+\frac{255}{256x^2y^2}+2 \geq \frac{1}{8}+ \frac{255}{256\frac{(x+y)^4}{16}} +2=\frac{289}{16} \Leftrightarrow x=y=\frac{1}{2}[/TEX]
Bài này?
ChoChứng minh rằng

Bđt cần cm tương đương:
[TEX](a-\frac{{a}^{3}}{{a}^{2}+{b}^{2}}+...\leq \frac{a+b+c}{2} \Leftrightarrow \frac{a{b}^{2}}{{a}^{2}+{b}^{2}}+...\leq \frac{a+b+c}{2} [/TEX]
ta có:[TEX]\frac{a{b}^{2}}{{a}^{2}+{b}^{2}}=b.(\frac{ab}{{a}^{2}+{b}^{2}})\leq b.\frac{({a}^{2}+{b}^{2})}{2({a}^{2}+{b}^{2})}\[/TEX]
tương tự ta cộng các vế là được điều phải chứng minh>-
>-
>-
>-
>-
>-
>-
bạn thử nháp kĩ lại xem!! chỉ cần chuyển vế trái sang phải rùi + vào 2 vê (a+b+c)/2 là có điều đó mà!!!!
Bài này?
ChoChứng minh rằng

cho các số thực dương a,b,c CMR:
[TEX] \frac{a^3}{a^2 + ab + b^2 } + \frac{b^3}{b^2 + bc + c^2} + \frac{c^3}{c^2 + ac + a^2} \geq \frac{a+b+c}{3}[/TEX]
p\s: bài này không khó đâu!
Chứng minh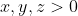

Cho tớ hỏi bài này, nhìn hơi lạ. Trong đề thi HSG Trung Quốc
Cho tam giác ABC nhọn, chứng minh
[TEX]\frac{cos^2 A}{cos A +1}[/TEX] + [TEX]\frac{cos^2 B}{cos B +1}[/TEX] + [TEX]\frac{cos^2 C}{cos C +1}[/TEX] [TEX]\geq[/TEX] [TEX]\frac{1}{2}[/TEX]

