- 30 Tháng sáu 2014
- 969
- 1,264
- 251
- Du học sinh
- YALE UNIVERSITY
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
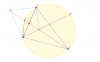
Giúp câu b,c hướng dẫn cách làm nha
câu b chưa biết cách cm góc bằng nhau
ra bằng nhau thì cm tứ giác nội tiếp đơn giản
còn câu c ko hiểu
mong dc chỉ giáo!!!