N
nhocngo976
CHo hs [TEX]y=\frac{x^2+x-3}{x+2} (C)[/TEX]
tìm trên Ox các điểm mà từ đó chỉ vẽ được đúng 1 tiếp tuyến đến C

tìm trên Ox các điểm mà từ đó chỉ vẽ được đúng 1 tiếp tuyến đến C
[TEX]y'=\frac{(4x-m)(x-1)-(2x^2-mx+m+6)}{(x-1)^2}[/TEX]
[TEX]x_1;x_2 \ la \ 2 \ nghiem \ cua \ pt \ u(x)=2x^2-mx+m+6=0\\---> u(x_1)=2x_1^2-mx_1+m+6=0 \ va \ u(x_2)=2x_2^2-mx_2+m+6=0[/TEX]
\Rightarrow[TEX]y'(x_1)=\frac{(4x_1-m)(x_1-1)}{(x_1-1)^2}[/TEX]
[TEX]y'(x_2)=\frac{(4x_2-m)(x_2-1)}{(x_2-1)^2}[/TEX]
[TEX]A ( a;0)[/TEX]CHo hs [TEX]y=\frac{x^2+x-3}{x+2} (C)[/TEX]
tìm trên Ox các điểm mà từ đó chỉ vẽ được đúng 1 tiếp tuyến đến C

nếu dạng này thì tớ nghĩ nên làm theo cách tớCậu thử mở cái của cậu ra xem , nó rút hết m đấy.
[TEX]y' = \frac{2(x-3)(x+1)}{(x-1)^2} ( x \not=1) [/TEX]
[TEX](C_m) \bigcap Ox = {A(a; 0) ; B(b;0) } [/TEX], [TEX]a, b \in (C_m)[/TEX] nên a và b là nghiệm của phương trình:
[TEX]2x^2 - mx + m+6 = 0 [/TEX]
[TEX]\Rightarrow \left{2( a+b) = m \\ 2ab = m+6 [/TEX]
[TEX]ycbt \Leftrightarrow y'(a) . y'(b) = - 1 \Leftrightarrow 4 ( a-3)(b-3)(a+1)(b+1) = - ( a-1)^2(b-1) ^2 \\ \Leftrightarrow 4( ab - 3( a+ b) + 9)( ab + a+ b =1) = - ( ab - (a+b) +1)^2[/TEX]
thế m vào ^^
[TEX]y'=\frac{(4x-m)(x-1)-(2x^2-mx+m+6)}{(x-1)^2}[/TEX]
[TEX]x_1;x_2 \ la \ 2 \ nghiem \ cua \ pt \ u(x)=2x^2-mx+m+6=0\\---> u(x_1)=2x_1^2-mx_1+m+6=0 \ va \ u(x_2)=2x_2^2-mx_2+m+6=0[/TEX]
\Rightarrow[TEX]y'(x_1)=\frac{(4x_1-m)(x_1-1)}{(x_1-1)^2}[/TEX]
[TEX]y'(x_2)=\frac{(4x_2-m)(x_2-1)}{(x_2-1)^2}[/TEX]
có thể áp dụng vào bài kia
TXD: D=R\{-2}CHo hs [TEX]y=\frac{x^2+x-3}{x+2} (C)[/TEX]
tìm trên Ox các điểm mà từ đó chỉ vẽ được đúng 1 tiếp tuyến đến C

tớ nghĩ thiếu trường hợp cậu ạ[TEX]A ( a;0)[/TEX]
\Leftrightarrowg[tex](x)=(1-a)x_o^2 + 2( 3 - 2a) x_o + 6 - 5a = 0 [/TEX]
[TEX]a=1 \ thoa.[/TEX]
[TEX]a \not=1, \Delta' = 0 ...[/TEX]
(*) Trả lời :Cho hs [tex]y=\frac{ax^2+bx+c}{dx+e} \ ( ad \ khac \ 0)[/tex] và tử khác mẫu
gọi C là đồ thì
Gọi [tex]x_o[/tex] là hoành độ giao điểm của C với Ox
CMR: hệ số góc tiếp tuyến tại x0 là: [tex]k=\frac{2ax_o+b}{dx_o+e}[/tex]
ra đáp số luôn nhé ^^ kt xem mik tính toán có đúng không)
câu c mọi người làm nếu có th thì giải thích giúp tớ nhá ^^ Cảm ơn nhiều
nghỉ + ngủ =))
(*) Trả lời : Bạn thử đặt [tex]{(x_A - 1)}^2 = t [/tex] xem sao .
tìm hai điểm A, B thuộc (C):sao cho tiếp tuyến kẻ từ A và B song song với nhau và thoả mãn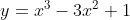
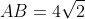
Mình làm rồi nhưng ra nghiệm lẻ, cụ thể là đến đây thì tắc:
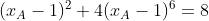
Các bác xem hộ cái(
nghiệm cũng lẻ
nhưng hình như khác cậu :-?
...
[TEX]AB^2= (x_B-x_A)^2+[x_B^3-x_A^3-3x_B^2+3x_A^2]^2=32[/TEX]
\Leftrightarrow[TEX](x_B-x_A)^2[(x_A+x_B)^2-3(x_A+x_B)-x_A.x_B+1]^2=32[/TEX]
(*) Bạn nói rõ câu hỏi hơn một tí được không
Cho [tex](C): y = \frac{x^2+4x-17}{x-3}[/tex] . Tìm [tex]M, N \in (C)[/tex] sao cho tại đó y' triệt tiêu. Viết phương trình MN
=> Có phải tại đó [tex]y' = 0[/tex] không ?
Trời mình gõ chữ y mà ^^
y'=0 hoặc y' không xác định
Cho h/s [TEX]y=f(x)=x-1+\frac{m-1}{x+1}[/TEX] có đồ thị [TEX](Cm)[/TEX]
Tìm điều kiện cần và đủ của [TEX]m[/TEX] để trên mặt phẳng tọa độ tồn tại ít nhất 1 điểm sao cho từ đó kẻ đc 2 tiếp tuyến với [TEX](Cm)[/TEX] và 2 tiếp tuyến vuông góc với nhau.
cho hs y=\frac{x^2}{x-1}
tìm tập hợp các điểm trên mftd mà từ đó vẽ được 2 tiếp tuyến đến C và 2 tiếp tuyến đó vuông góc với nhau

