[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
VÒNG TRÒN LƯỢNG GIÁC ĐA TRỤC TRONG DAO ĐỘNG CƠ
1/ Cơ sở lí thuyếtNhư chúng ta đã biết, mỗi dao động điều hòa được xem là hình chiếu của 1 chuyển động tròn đều trên 1 trục nằm trong mặt phẳng quỹ đạo, nghĩa là có thể dùng chuyển động tròn đều để biểu diễn 1 dao động điều hòa, hay đơn giản hơn là cho 1 vecto quay thì hình chiếu đầu mút vecto đó cũng sẽ biểu diễn 1 dao động điều hòa.
Tuy nhiên, trong nhiều bài toán có sự liên quan giữa cả li độ x, vận tốc v và gia tốc a, việc vẽ mỗi vòng tròn lượng giác để ứng với mỗi đại lượng trên sẽ rất mất thời gian và bất tiện. Thay vào đó, chúng ta có thể vẽ 1 vòng tròn nhưng có thể biểu diễn cả 3 đại lượng trên làm cho việc giải bài toán rất nhanh gọn, tiện lợi. Vòng tròn mà mình vừa nhắc đến có tên là VÒNG TRÒN LƯỢNG GIÁC ĐA TRỤC
2/ Cách vẽ vòng tròn lượng giác đa trục
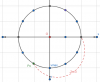
+ Vẽ vòng tròn
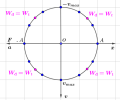
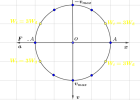
+ Ta chọn trục nằm ngang sang phải là trục li độ x

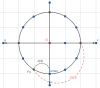
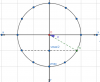
+ Vì vận tốc v vuông pha với li độ x nên có phương trình [imath]v=-wA.sin(wt+\varphi )[/imath], cộng thêm việc có dấu " - " ở trước nên trục v sẽ vuông góc với trục x và hướng xuống

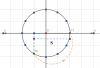
+ Tương tự, li độ a ngược pha với x nên trục a sẽ nằm ngang và hướng sang trái (ngược với trục x)
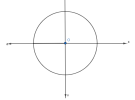
Vậy là chúng ta đã có 1 Vòng tròn lượng giác đa trục hoàn chỉnh
3/ Cách sử dụng vòng tròn lượng giác đa trục trong dao động cơ
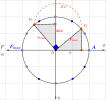
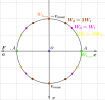
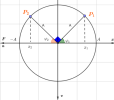
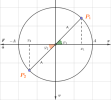
Ta cho vecto OM quay quanh O như hình vẽ, như trên cơ sở lí thuyết, nó sẽ biểu diễn 1 dao động điều hòa.
Ta sẽ áp dụng phương pháp vòng tròn lượng giác đa trục như sau:
+ Khi tính toán liên quan đến li độ x (ví dụ như tính li độ của vật, quãng đường vật đi được,...) thì bán kính vecto OM bằng [imath]xmax=A[/imath]
+ Khi tính toán lên quan đến vận tốc v (ví dụ tính vận tốc, từ phương trình vận tốc tìm pha ban đầu,...) thì bán kính vecto OM bằng [imath]vmax=wA[/imath]
+ Tương tự, khi tính toán liên quan đến gia tốc a (ví dụ tính gia tốc vật, xác định pha ban đầu qua phương trình gia tốc a,...) thì bán kính vecto OM bằng [imath]amax= w^2.A[/imath]
Để các bạn dễ hình dung hơn về phương pháp này, mình sẽ lấy 1 ví dụ đơn giản như sau:

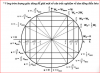
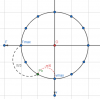
Ở hình trên, vecto quay OM có vị trí hợp với trục Ox 1 góc [imath]\alpha[/imath].
Yêu cầu: xác định li độ x, vận tốc v, gia tốc a của vật tại thời điểm đó. Các thông số [imath]w,A,\alpha[/imath] đã biết
Giải:
+ Ta chiếu vecto OM lên các trục Ox, Ov,Oa
+ Tính li độ x

Dễ thấy, từ M chiếu lên trục Ox thì hình chiếu M thuộc phần dương của trục Ox
Theo lí thuyết trên, khi tính toán liên quan đến li độ x, bán kính vecto OM bằng xmax = A
Ta dễ dàng suy ra [imath]x=Acos\alpha[/imath] bằng hệ thức lượng trong tam giác vuông
+ Tính vận tốc v
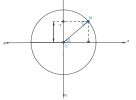
Ta cũng hạ đường vuông góc từ M lên trục Ov, nhận thấy hình chiếu của nó nằm ở phần âm trục Ov.
Mặt khác, khi tính toán liên quan vận tốc, vecto bán kính OM có độ dài bằng [imath]v_{max}=wA[/imath] (theo lí thuyết ở trên)
Kết hợp kiến thức hệ thức lượng trong tam giác vuông, dễ dàng suy ra: [imath]v=-OM.sin\alpha =-wA.sin\alpha[/imath] (dấu trừ vì hình chiếu M nằm ở phần âm trục Ov)
+ Tính li độ a
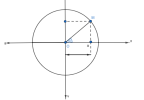
Tương tự tính x và v, ta cũng chiếu M lên trục Oa, dễ thấy hình chiếu nằm ở phần âm trục Oa
Theo lí thuyết trên, khi tính toán liên quan đến gia tốc, vecto bán kính OM có độ dài bằng [imath]amax=w^2.A[/imath]
Từ hệ thức lượng trong tam giác vuông suy ra: [imath]a=-OM.cos\alpha =-w^2.A.cos\alpha[/imath] (dấu trừ vì hình chiếu thuộc phần âm trục Oa)
Qua ví dụ trên các bạn đã hiểu hơn về phương pháp này chưa nhỉ
Hẹn gặp lại ở bài viết tiếp theo.....
À, trong lúc chờ bài tập vận dụng thì các bạn vào đây và đây để "giải khuây" nha
Last edited: