B
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
K
khanhtoan_qb
N
nguyenhoangthuhuyen
Theo tui giải thế này, bà con xem đúng h0k nhá (*)Tui mới nghĩ ra 2 TH mới, nhưng trong đó có 1TH không biết đúng không
- Nếu [TEX]2a = b hay a = \frac{b}{2} > 0[/TEX]
Thì (*) [TEX]= 0 - 2a - b = - 4a = - 2b[/TEX]
- Nếu [TEX]2a = b = 0 hay a = b = 0[/TEX]
Thì (*) [TEX]= 0 [/TEX] //
/
______đúng không nhỉ_______/
/
/

C = [TEX]a. \frac{\sqrt{4a^2-4ab+b^2}{a^2}}[/TEX] [TEX]- 2a - b[/TEX]
C = [TEX]a. \frac{\sqrt{(2a-b)^2}{a^2}[/TEX] [TEX] - 2a - b[/TEX]
C = [TEX]a. \frac{\sqrt({2a-b}{a})^2[/TEX] [TEX] -2a - b[/TEX]
C = [TEX]\left [ \frac{2a-b}{a} \right ] [/TEX] [TEX]- 2a - b[/TEX]
Ta có:
[TEX]\frac{2a-b}{a}[/TEX] \geq 0
\Leftrightarrow [TEX]\left[\begin{\left{\begin{2a-b\geq0}\\{a > 0} }\\{\left{\begin{2a-b \leq0}\\{a<0} } [/TEX]
Giai? ra nhé
TH1: + [TEX]2a>b; a>0 [/TEX]
TH2: + [tex]2a>b; a<0 [/tex]
TH3: + [tex] 2a<b; a>0[/tex]
TH4: + [tex]2a<b; a<0[/tex]
Bốn trường hợp tự giả
p/s: haizzzzzzzzzzzzz................ Mệt, k bik đúng hay sai, bà con xem giùm nhé
K
khanhtoan_qb
Nhờ các mod del hộ em cái, do em chưa được có khả năng nên nhờ các mod nha 
Last edited by a moderator:
K
khanhtoan_qb
Sai rùi bạn ạTheo tui giải thế này, bà con xem đúng h0k nhá (*)
C = [TEX]a. \frac{\sqrt{4a^2-4ab+b^2}{a^2}}[/TEX] [TEX]- 2a - b[/TEX]
C = [TEX]a. \frac{\sqrt{(2a-b)^2}{a^2}[/TEX] [TEX] - 2a - b[/TEX]
C = [TEX]a. \frac{\sqrt({2a-b}{a})^2[/TEX] [TEX] -2a - b[/TEX]
C = [TEX]\left [ \frac{2a-b}{a} \right ] [/TEX] [TEX]- 2a - b[/TEX]
Ta có:
[TEX]\frac{2a-b}{a}[/TEX] \geq 0
\Leftrightarrow [TEX]\left[\begin{\left{\begin{2a-b\geq0}\\{a > 0} }\\{\left{\begin{2a-b \leq0}\\{a<0} } [/TEX]
Giai? ra nhé
TH1: + [TEX]2a>b; a>0 [/TEX]
TH2: + [tex]2a>b; a<0 [/tex]
TH3: + [tex] 2a<b; a>0[/tex]
TH4: + [tex]2a<b; a<0[/tex]
Bốn trường hợp tự giả
p/s: haizzzzzzzzzzzzz................ Mệt, k bik đúng hay sai, bà con xem giùm nhé
Đề là như thế này nè
[TEX]C = a. \sqrt{\frac{4a^2-4ab+b^2}{a}} - 2a - b[/TEX]
Chứ có phải là
[TEX] C = a. {\sqrt{\frac{4a^2-4ab+b^2}{a^2}}- 2a - b[/TEX] đâu
khác nhau hoàn toàn đó, hèn gì, bạn cứ bảo là có 4 cách, sai bét bèn bẹt đi chứ
Last edited by a moderator:
A
asroma11235
DKXD:Thử bài này nha:
Tìm x biết:
[TEX]\sqrt{x^2 - 2x + 1} + \sqrt{x^2 - 4x + 4} = x - 3[/TEX]
=> PT vô nghiệm!!!
p/s: Bài trên chỉ có 2 TH
Last edited by a moderator:
M
maricosa
Thử bài này nha:
Tìm x biết:
[TEX]\sqrt{x^2 - 2x + 1} + \sqrt{x^2 - 4x + 4} = x - 3[/TEX]
[TEX]\sqrt{x^2 - 2x + 1} + \sqrt{x^2 - 4x + 4} = x - 3[/TEX] ( ĐK : x \geq 3)
\Leftrightarrow[TEX]\sqrt{(x-1)^2} + \sqrt{(x-2)^2} = x - 3[/TEX]
\Leftrightarrow[TEX] |x-1| + |x-2| = x - 3 [/TEX]
Xét các trường hợp :
Với x<1 thì x-1 < 0 và x-2 < 0, ta có phương trình
1- x + 2 - x = x- 3 \Leftrightarrow x= 2 ( Loại )
Với [TEX]1 \leq x \leq 2 [/TEX] thì x- 1 \geq 0 và x-2 \leq 0, ta có phương trình sau ;
x- 1 + 2 - x = x - 3 \Leftrightarrow x = 2 ( Loại khi kết hợp vs ĐK chung)
Với x> 2 thì x- 1 > 0 , x-2 > 0 ta có phương trình
x- 1 + x - 3 = x - 3 \Leftrightarrow x = 1 ( Loại )
Vậy pt vô nghiệm!
Mọi ng` xem thế nào ha !
Last edited by a moderator:
N
nguyenhoangthuhuyen
p/s: sr all, đề là [tex] a^2 [/tex]
Thui chuyển tiếp bài khác nhá
Biểu thức sau đây xác định vs giá trị nào của x?
a) [tex] \sqrt{x-1}.\sqrt{x-2} [/tex]
b) [tex] \sqrt{x^2-4}[/tex]
Thui chuyển tiếp bài khác nhá
Biểu thức sau đây xác định vs giá trị nào của x?
a) [tex] \sqrt{x-1}.\sqrt{x-2} [/tex]
b) [tex] \sqrt{x^2-4}[/tex]
Last edited by a moderator:
N
nguyenhoangthuhuyen
sao lại đặt điều kiện xác định là x \geq3DKXD:
^2}+\sqrt{(x-2)^2}=x-3)
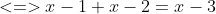

=> PT vô nghiệm!!!
p/s: Bài trên chỉ có 2 TH
mình k hiểu lắm
K
khanhtoan_qb
bạn giải sai rùi tề, đã có đièu kiện là x \geq 3[TEX]\sqrt{x^2 - 2x + 1} + \sqrt{x^2 - 4x + 4} = x - 3[/TEX] ( ĐK : x \geq 3)
\Leftrightarrow[TEX]\sqrt{(x-1)^2} + \sqrt{(x-2)^2} = x - 3[/TEX]
\Leftrightarrow[TEX] |x-1| + |x-2| = x - 3 [/TEX]
Xét các trường hợp :
Với x<1 thì x-1 < 0 và x-2 < 0, ta có phương trình
1- x + 2 - x = x- 3 \Leftrightarrow x= 2 ( Loại )
Với [TEX]1 \leq x \leq 2 [/TEX] thì x- 1 \geq 0 và x-2 \leq 0, ta có phương trình sau ;
x- 1 + 2 - x = x - 3 \Leftrightarrow x = 2 ( Loại khi kết hợp vs ĐK chung)
Với x> 2 thì x- 1 > 0 , x-2 > 0 ta có phương trình
x- 1 + x - 3 = x - 3 \Leftrightarrow x = 1 ( Loại )
Vậy pt vô nghiệm!
Mọi ng` xem thế nào ha !
Vậy sao lại xét x < 1, và các TH khác nữa vô lí
Điều kiện xác địnhp/s: sr all, đề là [tex] a^2 [/tex]
Thui chuyển tiếp bài khác nhá
Biểu thức sau đây xác định vs giá trị nào của x?
a) [tex] \sqrt{x-1}.\sqrt{x-2} [/tex]
b) [tex] \sqrt{x^2-4}[/tex]
a) xác định \Leftrightarrow [TEX]x - 1 \geq 0...vs... x - 2 \geq 0 \Leftrightarrow x \geq 1...vs...x \geq 2\Rightarrow x \geq2[/TEX]
b) xác định \Leftrightarrow [TEX]x^2 - 4 \geq 0 \Leftrightarrow x^2 \geq 4 \Leftrightarrow x \geq 2...hoac...x \leq - 2[/TEX]
ta có [TEX]\sqrt{x^2 - 2x + 1} + \sqrt{x^2 - 4x + 4} = x - 3[/TEX]sao lại đặt điều kiện xác định là x \geq3
mình k hiểu lắm
nhận thấy [TEX]\sqrt{x^2 - 2x + 1} \geq 0[/TEX]với mọi x
[TEX]\sqrt{x^2 - 4x + 4} \geq 0[/TEX]với mọi x
\Rightarrow[TEX]\sqrt{x^2 - 2x + 1} + \sqrt{x^2 - 4x + 4} \geq 0 \Rightarrow x - 3 \geq 0 \Rightarrow x \geq 3[/TEX]
L
linhhuyenvuong
________________________sao lại đặt điều kiện xác định là x \geq3
mình k hiểu lắm
[TEX]\sqrt{x^2-2x+1} +\sqrt{x^2-4x+4} =x-3[/TEX]
[TEX]\sqrt{x^2-2x+1}+\sqrt{x^2-4x+4} \geq 0[/TEX]
\Rightarrow[TEX]x-3 \geq 0[/TEX]
\Rightarrow[TEX]x\geq3[/TEX]
P
phuocbig
So sánh
+ [tex]A=\sqrt{7-4\sqrt{3}} [/tex] và [tex]B=\sqrt{17-12\sqrt{2}}[/tex]
+ [tex]E=\sqrt{2-\sqrt{3}}[/tex] và [tex]F=\sqrt{3-\sqrt{5}}[/tex]
+ [tex]I=\sqrt{9+4\sqrt{5}}+\sqrt{9-4\sqrt{5}}[/tex] và [tex]J=\frac{1}{\sqrt{9+4\sqrt{5}}}+\frac{1}{\sqrt{9-4\sqrt{5}}}[/tex]
+ [tex]A=\sqrt{7-4\sqrt{3}} [/tex] và [tex]B=\sqrt{17-12\sqrt{2}}[/tex]
+ [tex]E=\sqrt{2-\sqrt{3}}[/tex] và [tex]F=\sqrt{3-\sqrt{5}}[/tex]
+ [tex]I=\sqrt{9+4\sqrt{5}}+\sqrt{9-4\sqrt{5}}[/tex] và [tex]J=\frac{1}{\sqrt{9+4\sqrt{5}}}+\frac{1}{\sqrt{9-4\sqrt{5}}}[/tex]
K
khanhtoan_qb
Ta có:So sánh
+ [tex]I=\sqrt{9+4\sqrt{5}}+\sqrt{9-4\sqrt{5}}[/tex] và [tex]J=\frac{1}{\sqrt{9+4\sqrt{5}}}+\frac{1}{\sqrt{9-4\sqrt{5}}}[/tex]
[TEX]J = \frac{\sqrt{9 + 4\sqrt{5}} + \sqrt{9 - 4\sqrt{5}}}{\sqrt{81 - 16 . 5}} = \frac{I}{\sqrt{1}}= I[/TEX]
\Rightarrow[TEX]I = J [/TEX]
L
locxoaymgk
So sánh
+ [tex]A=\sqrt{7-4\sqrt{3}} [/tex] và [tex]B=\sqrt{17-12\sqrt{2}}[/tex]
+ [tex]E=\sqrt{2-\sqrt{3}}[/tex] và [tex]F=\sqrt{3-\sqrt{5}}[/tex]
+ [tex]I=\sqrt{9+4\sqrt{5}}+\sqrt{9-4\sqrt{5}}[/tex] và [tex]J=\frac{1}{\sqrt{9+4\sqrt{5}}}+\frac{1}{\sqrt{9-4\sqrt{5}}}[/tex]
1,
Vì [TEX]80\sqrt{3}<140[/TEX]
[TEX]\Rightarrow 148+80\sqrt{3} <148+140[/TEX]
[TEX]\Rightarrow (10+4\sqrt{3})^2 <288[/TEX]
[TEX]\Rightarrow 10+4\sqrt{3}<12\sqrt{2}[/TEX]
[TEX]\Rightarrow -10-4\sqrt{3}> -12\sqrt{2}[/TEX]
[TEX] \Rightarrow 7-4\sqrt{3}>17-12\sqrt{2}[/TEX]
[TEX] \Rightarrow dpcm.[/TEX]
2,
Ta có : Ta có[TEX] 1<2\sqrt{3}\Rightarrow 5<1+3+2\sqrt{3}=(\sqrt{3}+1)^2[/TEX]
[TEX] \Rightarrow \sqrt{5} <\sqrt{3}+1[/TEX]
[TEX] \Rightarrow \sqrt{5}-\sqrt{3}-1 <0[/TEX]
[TEX] \Rightarrow 2-\sqrt{3}-3+\sqrt{5} <0[/TEX]
[TEX] \Rightarrow 2-\sqrt{3}<3-\sqrt{5}[/TEX]
[TEX] \Rightarrow dpcm[/TEX]
Last edited by a moderator:
P
phuocbig
Thanks 2 bạn trên nhiều nhá ^^!
giúp dùm mình 2 bài này luôn
Thu gọn:
[tex]\sqrt{21+6\sqrt{6}}+\sqrt{9+3\sqrt{8}}-\sqrt{6+3\sqrt{3}}[/tex]
Tính
[tex]\frac{-23}{\sqrt{6}+\sqrt{3}+\sqrt{5}}-\frac{6}{\sqrt{3}-\sqrt{2}}+\frac{1}{\sqrt{3}+\sqrt{2}}-\frac{5\sqrt{6}}{\sqrt{6}-1}[/tex]
giúp dùm mình 2 bài này luôn
Thu gọn:
[tex]\sqrt{21+6\sqrt{6}}+\sqrt{9+3\sqrt{8}}-\sqrt{6+3\sqrt{3}}[/tex]
Tính
[tex]\frac{-23}{\sqrt{6}+\sqrt{3}+\sqrt{5}}-\frac{6}{\sqrt{3}-\sqrt{2}}+\frac{1}{\sqrt{3}+\sqrt{2}}-\frac{5\sqrt{6}}{\sqrt{6}-1}[/tex]
Last edited by a moderator:
L
locxoaymgk
Thanks 2 bạn trên nhiều nhá ^^!
giúp dùm mình 2 bài này luôn
Thu gọn:
[tex]\sqrt{21+6\sqrt{6}}+\sqrt{9+3\sqrt{8}}-\sqrt{6+3\sqrt{3}}[/tex]
Tính
[tex]\frac{-23}{\sqrt{6}+\sqrt{3}+\sqrt{5}}-\frac{6}{\sqrt{3}-\sqrt{2}}+\frac{1}{\sqrt{3}+\sqrt{2}}-\frac{5\sqrt{6}}{\sqrt{6}-1}[/tex]
Bài 1 Mình thấy có vấn đề :
Mình sửa lại theo cách của mình :
Ta có [tex]\sqrt{21+6\sqrt{6}}+\sqrt{19+3\sqrt{8}}-\sqrt{6+3\sqrt{3}}[/tex]
[TEX]= \sqrt{(3\sqrt{2}+\sqrt{3})^2}+\frac{1}{\sqrt{2}}.\sqrt{(\sqrt{6}+\sqrt{2})^2}-\frac{1}{\sqrt{2}}.\sqrt{(3+\sqrt{3})^2}[/TEX]

\Rightarrow .......................................
Vậy mình đã sửa 9 thành 19 bạn xem lại đề đi!!
Bài 1 tớ thấy có vấn đề , nên đổi 9 \Rightarrow 19 thì đúng hơn!!
P/s : lần sau U đừng có gửi 2 bài có đề trùng nhau nữa!! @};-@};-
K
khanhtoan_qb
Thanks 2 bạn trên nhiều nhá ^^!
giúp dùm mình 2 bài này luôn
Thu gọn:
[tex]\sqrt{21+6\sqrt{6}}+\sqrt{9+3\sqrt{8}}-\sqrt{6+3\sqrt{3}}[/tex]
Tính
[tex]\frac{-23}{\sqrt{6}+\sqrt{3}+\sqrt{5}}-\frac{6}{\sqrt{3}-\sqrt{2}}+\frac{1}{\sqrt{3}+\sqrt{2}}-\frac{5\sqrt{6}}{\sqrt{6}-1}[/tex]
Bài 2:
Đầu tiên phảu trục căn thức ở các mẫu số
Ta có:
[TEX]\frac{-23}{\sqrt{6} + \sqrt{3} + \sqrt{5}} = \frac{-23(\sqrt{6} + \sqrt{3} - \sqrt{5})}{(\sqrt{6} + \sqrt{3})^2 - 5} = \frac{-23(\sqrt{6} + \sqrt{3} - \sqrt{5})}{2(2 + \sqrt{18})} = \frac{-23(\sqrt{6} + \sqrt{3} - \sqrt{5})(2 - \sqrt{18})}{2. (4 - 18)} = \frac{23\sqrt{6} + 92\sqrt{3} + 46\sqrt{5} + 69\sqrt{10}}{(-28)}[/TEX]
[TEX]\frac{-6}{\sqrt{3} - \sqrt{2}} = -6\sqrt{3} - 6\sqrt{2}[/TEX]
[TEX]\frac{1}{\sqrt{3} + \sqrt{2}} = \sqrt{3} - \sqrt{2}[/TEX]
[TEX]\frac{-5\sqrt{6}}{\sqrt{6} - 1} = (-\sqrt{6}).(\sqrt{6} + 1) = (-\sqrt{6}) - 6[/TEX]
\Rightarrow [TEX]A = \frac{51\sqrt{6} + 232\sqrt{3} + \sqrt{62 + 69}.\sqrt{5} + 196\sqrt{2} + 168}{(-28)}[/TEX]
p/s gõ talex mỏi cả tay nhưng không biết có đúng không ta, số không có tròn gì cả
=o=o=o=o=o=o=o=o=o=o=o=o=o=o==o=o=o=o=o=o=o=o=o=o=o=o=o=o=o=o=
N
nguyenhoangthuhuyen
Thui
chuyển tiếp đê bà com
Chém nào
Xác định giá trị biểu thức
[TEX]\frac{1}{\sqrt{2}+\sqrt{1} [/TEX] [TEX]+[/TEX] [TEX]\frac{1}{\sqrt{3}+\sqrt{2} [/TEX][TEX]+[/TEX] [TEX]\frac{1}{\sqrt{4}+\sqrt{3}[/TEX]
chuyển tiếp đê bà com
Chém nào
Xác định giá trị biểu thức
[TEX]\frac{1}{\sqrt{2}+\sqrt{1} [/TEX] [TEX]+[/TEX] [TEX]\frac{1}{\sqrt{3}+\sqrt{2} [/TEX][TEX]+[/TEX] [TEX]\frac{1}{\sqrt{4}+\sqrt{3}[/TEX]
Last edited by a moderator:
D
duynhan1
[TEX]=\sqrt{4}-\sqrt{1} = 1 [/TEX] :-??Thui
chuyển tiếp đê bà com
Chém nào
Xác định giá trị biểu thức
[TEX]\frac{1}{\sqrt{2}+\sqrt{1}[/TEX] + [TEX]\frac{1}{\sqrt{3}+\sqrt{2}[/TEX] + [TEX]\frac{1}{\sqrt{4}+\sqrt{3}[/TEX]
P/s: Bạn chú ý các CT trên cùng 1 hàng nên đặt chung vào 1 thẻ

P
phuocbig
đề bài của mình chả gì sai cả , mình cũng giải ra rồi , tks mấy bạn 

bạn giải sai rùi=o=o=o=o=o=o=o=o=o=o=o=o=o=o==o=o=o=o=o=o=o=o=o=o=o=o=o=o=o=o=
Last edited by a moderator:

