- 28 Tháng hai 2017
- 4,472
- 5,490
- 779
- Hà Nội
- THPT Đồng Quan
nick này chỉ có mk dùng thôi nha bạn chỉ là mk có đọc thêm sách + thêm 1 chút liều lĩnh khi làm bừa ^^thế nick này nhiều người cầy à
nick này chỉ có mk dùng thôi nha bạn chỉ là mk có đọc thêm sách + thêm 1 chút liều lĩnh khi làm bừa ^^thế nick này nhiều người cầy à
Chuẩn rồi. @Nữ thần không phải học lớp 8 đâu. Chém đấy. 80 tuôi còn học lớp 8 gì nữa.^^@Nữ Thần Mặt Trăng lớp 8????????? Chém vừa thôi má. Má còn làm bài lp 10 nx mà.
cần bài cuối mà ba lại làm 2 bài dễ ( con đã làm)Góp vui:
Bài 7:
$x+y-2(\sqrt{x}+\sqrt{y})+2 \geq 0
\\\Rightarrow x-2\sqrt{x}+1+y-2\sqrt{y}+1\geq 0
\\\Rightarrow (\sqrt{x}-1)^2+(\sqrt{y}-1)^2 \geq 0$.
Dấu '=' khi $x=y=1$.
Bài 8:
Cách 1:Áp dụng bđt cauchy-schawz dạng engel ta có:
$\sum \dfrac{a^2}{a+b} \geq \dfrac{(a+b+c)^2}{2(a+b+c)}=\dfrac{a+b+c}{2}=\dfrac{1}{2}$
Cách 2:
$\dfrac{a^2}{b+c}+\dfrac{b+c}{4} \geq a$
Cộng vế theo vế là được dpcm.
hôm trc ta bảo 80 tuổi thì nói 80 tuổi mới học lớp 8 giờ thế này đâyChuẩn rồi. @Nữ thần không phải học lớp 8 đâu. Chém đấy. 80 tuôi còn học lớp 8 gì nữa.^^
Cũng phải có bài dễ, bài khó chứ bạn. Bạn giải chi tiết ra để mọi người cùng tham khảo nào !bài 7: ?? dành cho lớp 7 à
bài 8 áp dụng cauchy schwarz dạng engel là ra luôn
hoặc áp dụng bđt cô si phân thức 1 vs 1/4(a+b) tương tự
Bạn ơi bạn đánh sai số thứ tự rồi, ở trên có Bài 9 rồi mà. Nhờ mod @Nguyễn Xuân Hiếu sửa giúp ạ !Bài 9: Cho các số thực dương x,y thỏa mãn [tex](x+y-1)^{2}=xy[/tex]. Tìm GTNN của biểu thức
P= [tex]\frac{1}{xy}+\frac{1}{x^{2}+y^{2}}+\frac{\sqrt{xy}}{x+y}[/tex]
Bài10: Cho [tex]1\leqslant a,b\leqslant 2[/tex] .Tìm GTNN của
A= [tex]\frac{(a+b)^{2}}{a^{3}+b^{3}}[/tex]
mình không hiểu bước đầu bạn giải thích rõ cho mình vsBài 9:
$P=\dfrac{2}{\sqrt{(2x+y)^3+1}-1}
\\P=\dfrac{2}{\sqrt{(2x+y+1)(4x^2+4xy+y^2-2x-y+1)}-1}
\\\geq \dfrac{2}{\dfrac{2x+y+1+4x^2+4xy+y^2-2x-y+1}{2}-1}
\\=\dfrac{4}{4x^2+4xy+y^2}
\\=\dfrac{4}{(2x+y)^2}$.
Đặt $2x+y=a,2y+x=b$.
Khi đó:
$\dfrac{4}{a^2}+\dfrac{4}{b^2}+\dfrac{ab}{4}-\dfrac{8}{a+b} \\=2(\dfrac{1}{a^2}+\dfrac{1}{b^2})-\dfrac{8}{a+b}+(\dfrac{2}{a^2}+\dfrac{2}{b^2}+\dfrac{ab}{8}+\dfrac{ab}{8}) \\\geq (\dfrac{1}{a}+\dfrac{1}{b})^2-\dfrac{8}{a+b}+4.\sqrt[4]{\dfrac{2}{a^2}.\dfrac{2}{b^2}.\dfrac{ab}{8}.\dfrac{ab}{8}} \\\geq (\dfrac{16}{(a+b)^2}+1)-1-\dfrac{8}{a+b}+2 \\\geq \dfrac{8}{a+b}-\dfrac{8}{a+b}+1=1$
Dấu '=' khi $x=y=\dfrac{2}{3}$....
@ hỏi nhầm bàimình không hiểu bước đầu bạn giải thích rõ cho mình vs
Phân tích hđt:$a^3+b^3=(a+b)(a^2-ab+b^2)$.
$(2x+y)^3+1^3=....$
@Nguyễn Xuân Hiếu
Bài 10:Bài 10: Cho các số thực dương x,y thỏa mãn [tex](x+y-1)^{2}=xy[/tex]. Tìm GTNN của biểu thức
P= [tex]\frac{1}{xy}+\frac{1}{x^{2}+y^{2}}+\frac{\sqrt{xy}}{x+y}[/tex]
Bài11: Cho [tex]1\leqslant a,b\leqslant 2[/tex] .Tìm GTNN của
A= [tex]\frac{(a+b)^{2}}{a^{3}+b^{3}}[/tex]
Sao bạn lại nghĩ vậy nhỉ ?! Có bài BĐT khó thật sự, nhưng cũng có những bài đơn giản mà. Chỉ cần có kiến thức căn bản và luyện tập nhiều sẽ làm tốt thôi. Cũng cần có niềm đam mê và chăm chỉ nữaBất đẳng thức chả bh hi vọng làm được
quan trọng là khi thi thì cái BĐT khó thực sự còn khi học thì làm rất sungCó bài BĐT khó thật sự, nhưng cũng có những bài đơn giản
Thường đi thi bài BĐT là bài để lấy điểm 9,5 -10 màquan trọng là khi thi thì cái BĐT khó thực sự còn khi học thì làm rất sung
Khó quá, bài 11 nghĩ ra Min=1 rùi mà chẳng biết làm thế nào, đúng là cơm đến miệng mà chẳng biết ăn, ngày mai thi thử rùi làm thế nào bây giờ. Chắc là điểm rơi rồiBài11: Cho.Tìm GTNN của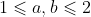
A=^{2}}{a^{3}+b^{3}})
Có vẻ như cái giả thiết 1=< a,b =< 2 là mấu chốt.Khó quá, bài 11 nghĩ ra Min=1 rùi mà chẳng biết làm thế nào, đúng là cơm đến miệng mà chẳng biết ăn, ngày mai thi thử rùi làm thế nào bây giờ. Chắc là điểm rơi rồi

