V
vansang02121998
- Ta có

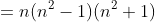
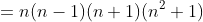
vì n; n+1 là 2 số nguyên liên tiếp


+; Nếu n = 5k ( k
 Z )
Z )

+; Nếu n = 5k
 1 ( k
1 ( k
 Z )
Z )

+; Nếu n = 5k
 2 ( k
2 ( k
 Z )
Z )


mà ƯCLN(2;5)=1

 đpcm
đpcm
Lâu lắm không có bài hình nhỉ
Bài 54: Cho hình vuông ABCD, điểm M nằm trên đường chéo AC. Gọi E; F theo thứ tự là các hình chiếu của M trên AD; CD. Chứng minh BM; AF; CE đồng quy
+12đ
vì n; n+1 là 2 số nguyên liên tiếp
+; Nếu n = 5k ( k
+; Nếu n = 5k
+; Nếu n = 5k
mà ƯCLN(2;5)=1
Lâu lắm không có bài hình nhỉ
Bài 54: Cho hình vuông ABCD, điểm M nằm trên đường chéo AC. Gọi E; F theo thứ tự là các hình chiếu của M trên AD; CD. Chứng minh BM; AF; CE đồng quy
+12đ
Last edited by a moderator: