[Toán 7]Rung chuông vàng

[soicon_boy_9x]

Tiếp nè.1 bài hình nha bà con
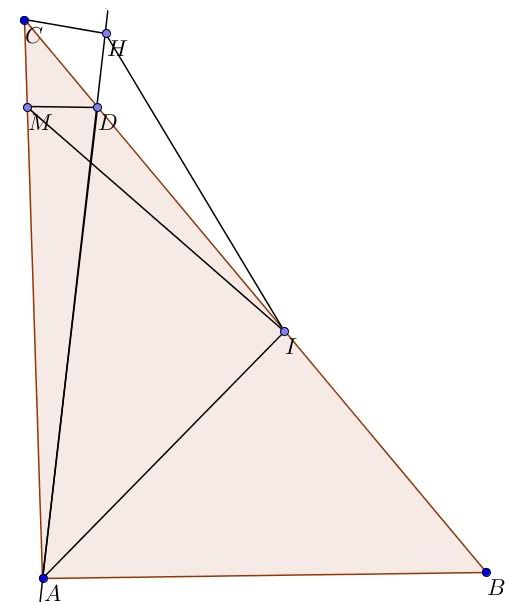
Cho 2 điểm A và B nằm cùng 1 mặt phẳng bờ d.Tìm M sao cho AM+MB bé nhất
Gợi ý:Trong 1 tam giác ,tổng 2 cạnh luôn lơn hơn cạnh còn lại

 

[nuhoangachau]

Nối AB cắt d tại M. (1)
Ta dễ dàng chứng minh được điểm đó thỏa mãn bài toán.
Trên d lấy một điểm M' từ M' kẽ M'A và M'B khác phía. (2)
Từ (1) và (2):

M'A + M'B

AB ( 3)
Mà: AB = MA + MB (4)
Từ (3) và (4):
M'A + M'B

AB = MA + MB
Dấu " = " xảy ra khi và chỉ khi:
M

M' ( M trùng M' ).
​

 

[soicon_boy_9x]

Tiếp tục tỉ lệ thức này:
Cho x,y,z khác 0 và biết:
[TEX]x^2=yz[/TEX]
[TEX]y^2=xz[/TEX]
[TEX]z^2=xy[/TEX]
Chứng minh rằng x=y=z

 

[braga]

Cộng 3 cái lại , ta được:

[TEX]x^2+y^2+z^2 = yz+xz+xy[/TEX]

Nhận thấy: [TEX]x^2+y^2+z^2 \geq yz+xz+xy[/TEX] dấu bằng xảy ra [TEX]\Leftrightarrow x=y=z \Rightarrow dpcm[/TEX]

 

[soicon_boy_9x]

Thêm 1 cách nữa đúng chủ đề mình đi các bác
Tỉ lệ thức

 

[harrypham]

Cách này có phần dài dòng, không biết có được không.

+ [TEX]x^2=yz \rightarrow \frac{x}{y}= \frac{z}{x} \ \ \ \ \ (1)[/TEX].
+ [TEX]y^2=xz \rightarrow \frac{x}{y}= \frac{y}{z} \ \ \ \ \ \ \ (2)[/TEX].
+ [TEX]z^2=xy \rightarrow \frac{x}{y}= \frac{z^2}{y^2} \ \ \ \ (3)[/TEX].

Nhân (1), (2) và (3) thì [TEX]\left( \frac{x}{y} \right)^3 = \frac{z}{x}. \frac{y}{z}. \frac{z^2}{y^2}= \frac{z^2}{xy}=1[/TEX]
[TEX]\Rightarrow x=y \Rightarrow \fbox{x=y=z}[/TEX].

 

[harrypham]

Bài mới. Cho một tam giác có độ dài ba cạnh là [TEX]4,12,x[/TEX]. Biết [TEX]x \in \mathbb{N}[/TEX]. Tìm [TEX]x[/TEX].

 

[minhtuyb]

Bài mới. Cho một tam giác có độ dài ba cạnh là [TEX]4,12,x[/TEX]. Biết [TEX]x \in \mathbb{N}[/TEX]. Tìm [TEX]x[/TEX].

-Vì [TEX]12,4,x[/TEX] là độ dài 3 cạch của 1 tam giác nên áp dụng BĐT [TEX]a-b<c<a+b[/TEX], ta có: [TEX]12-4<x<12+4 \Leftrightarrow 8<x<16[/TEX]
- Vì [TEX]x \in \mathbb{N}[/TEX] nên [TEX]x \in {9,10,11,12,13,14,15}[/TEX]
Bạn viết thiếu dữ kiện j` ko nhỉ @-)@-)@-)

 

[harrypham]

Xin lỗi, chữa lại đề, [TEX]4,12,x[/TEX] là ba đường cao của tam giác.
P/s: Tuy nhiên, nhìn hướng giải thì bạn đúng.

 

[soicon_boy_9x]

Mình đoán bài này áp dụng định lí Pi-Ta-Go là tổng bình phương 2 cạnh góc vuông bằng bình phương cạnh huyền

 

[braga]

1 số bài toán về số chính phương

Bài 1: Tìm tất cả bộ số nguyên dương (x,y,z) sao cho:

[TEX]x^2+y^2+z^2+2xy+2x(z-1)+2y(z+1)[/TEX] là số chính phương.

Bài 2: Chứng minh số [TEX]3^n+63[/TEX] không chính phương [TEX](n \in N;n \not= 0,4)[/TEX]

Bài 3: Tìm a để [TEX]17a+8[/TEX] là số chính phương.

 

[soicon_boy_9x]

Bài 1: Tìm tất cả bộ số nguyên dương (x,y,z) sao cho:

[TEX]x^2+y^2+z^2+2xy+2x(z-1)+2y(z+1)[/TEX] là số chính phương.

Bài 2: Chứng minh số [TEX]3^n+63[/TEX] không chính phương [TEX](n \in N;n \not= 0,4)[/TEX]

Bài 3: Tìm a để [TEX]17a+8[/TEX] là số chính phương.

Các bạn có thể tham khảo bài này tại chuyên đề số chính phương
http://www.scribd.com/doc/4343478/S-chinh-phng
Đây là những dạng toán để rèm lụn phương pháp làm

 

[braga]

1. Chứng minh:[TEX]\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n}[/TEX] không phải là số tự nhiên.

Đặt [TEX]A=\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n}[/TEX]

Giả sử [FONT=LaTeXRender_Math]k là số tự nhiên lớn nhất sao cho [/FONT][TEX]2^k \leq n \Rightarrow 2,3,4,....,n[/TEX] không có số nào chia hết cho [TEX]2^{k+1}[/TEX] Gọi P là tích tất cả các số từ 2 đến n và P không chia hết cho 2.
Giả sử, A là số tự nhiên , ta có:

[TEX]2^{k-1}PA=2^{k-1}P(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n})=\frac{2^{k-1}P}{2}+\frac{2^{k-1}P}{3}+.......+\frac{2^{k-1}P}{2^k}+........+\frac{2^{k-1}P}{n}[/TEX]

[TEX]\rightarrow \frac{2^{k-1}P}{2^k}=2^{k-1}PA-\frac{2^{k-1}P}{2}-\frac{2^{k-1}P}{3}-......-\frac{2^{k-1}P}{n}[/TEX]

Theo định nghĩa của P [TEX]\Rightarrow \frac{2^{k-1}P}{2^k}[/TEX] là số nguyên ( vô lí )

\Rightarrow A không phải là số nguyên \Rightarrow dpcm

Nguồn : diendantoanhoc.net
​

 

[soicon_boy_9x]

Tiếp bài nữa chứ anh em
Cho 2 điểm A,B nằm cùng 1 mặt phẳng bờ d
Tìm M trên đường thằng d sao cho AM+MB bé nhất

 

[hocmaitoanhoc]

Đặt [TEX]A=\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n}[/TEX]

Giả sử [FONT=LaTeXRender_Math]k là số tự nhiên lớn nhất sao cho [/FONT][TEX]2^k \leq n \Rightarrow 2,3,4,....,n[/TEX] không có số nào chia hết cho [TEX]2^{k+1}[/TEX] Gọi P là tích tất cả các số từ 2 đến n và P không chia hết cho 2.
Giả sử, A là số tự nhiên , ta có:

[TEX]2^{k-1}PA=2^{k-1}P(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n})=\frac{2^{k-1}P}{2}+\frac{2^{k-1}P}{3}+.......+\frac{2^{k-1}P}{2^k}+........+\frac{2^{k-1}P}{n}[/TEX]

[TEX]\rightarrow \frac{2^{k-1}P}{2^k}=2^{k-1}PA-\frac{2^{k-1}P}{2}-\frac{2^{k-1}P}{3}-......-\frac{2^{k-1}P}{n}[/TEX]

Theo định nghĩa của P [TEX]\Rightarrow \frac{2^{k-1}P}{2^k}[/TEX] là số nguyên ( vô lí )

\Rightarrow A không phải là số nguyên \Rightarrow dpcm​

Bài này có thể giải như sau:

Ta có: [TEX]A=\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n}=1:2+1:3+1:4+.....+1:n=1:(2+3+4+...+n)=\frac{1}{2+3+4+....+n}[/TEX]

Dĩ nhiên không phải số tự nhiên :-j:-j

 

[hiensau99]

[TEX]1:2+1:3+1:4+.....+1:n=1:(2+3+4+...+n)[/TEX]

T/c này sai hoàn toàn! VD tương tự:
[TEX]10:2+10:5=5+2=7 \neq \frac{10}{7}=10:7=10:(2+5)[/TEX]

 

[braga]

Tiếp nhể:

Bài toán: Cho dãy tỉ số bằng nhau: [TEX]\frac{2a+b+c+d}{a}=\frac{1+2b+c+d}{b}=\frac{a+b+2c+d}{c}=\frac{a+b+c+2d}{d}[/TEX]

Tính giá trị biểu thức : [TEX]M=\frac{a+b}{c+d}+\frac{b+c}{d+a}+\frac{c+d}{a+b}+\frac{d+a}{b+c}[/TEX]

 

[harrypham]

Tiếp nhể:

Bài toán: Cho dãy tỉ số bằng nhau: [TEX]\frac{2a+b+c+d}{a}=\frac{1+2b+c+d}{b}=\frac{a+b+2c+d}{c}=\frac{a+b+c+2d}{d}[/TEX]

Tính giá trị biểu thức : [TEX]M=\frac{a+b}{c+d}+\frac{b+c}{d+a}+\frac{c+d}{a+b}+\frac{d+a}{b+c}[/TEX]

Rảnh cho chém vài miếng.
Từ tỉ lệ thức đề bài ta có:
[TEX]\frac{2a+b+c+d}{a}-1=\frac{1+2b+c+d}{b}-1=\frac{a+b+2c+d}{c}-1=\frac{a+b+c+2d}{d}-1[/TEX]
[TEX]\Rightarrow \frac{a+b+c+d}{a}= \frac{a+b+c+d}{b}= \frac{a+b+c+d}{c}= \frac{a+b+c+d}{d} \ \ \ \ \ \ \ \ \ \ \ (*)[/TEX].

+ Nếu [TEX]a+b+c+d=0[/TEX] thì [TEX]a+b=-(c+d), \ b+c=-(d+a), \ c+d=-(a+b), \ d+a=-(b+c)[/TEX].

Thay các đẳng thức trên vào M thì ta được [TEX]M= \fbox{-4}[/TEX].

+ Nếu [TEX]a+b+c+d \neq 0[/TEX] thì [TEX](*) \Rightarrow a=b=c=d[/TEX].
Thay vào M thì [TEX]M= \fbox{4}[/TEX].

 

[braga]

Tiếp bài hình

Bài toán :Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho [TEX]ME=MA[/TEX], chưng minh:

a, [TEX]AC=EB[/TEX] và [TEX]AC//BE[/TEX]

b, Gọi I là 1 điểm trên AC, K là 1 điểm trên BE sao cho AI=EK Chưng minh 3 điểm I,M,K thẳng hàng.

c, Từ E kẻ [TEX]EH\perp BC(H\in BC)[/TEX]. Biết [TEX]\widehat{HBE}=50^o;\widehat{MEB}=25^o[/TEX]. Tính [TEX]\widehat{HEM}[/TEX] và [TEX]\widehat{MEB}[/TEX]

 

[harrypham]

Tiếp bài hình

Bài toán :Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho [TEX]ME=MA[/TEX], chưng minh:

a, [TEX]AC=EB[/TEX] và [TEX]AC//BE[/TEX]

b, Gọi I là 1 điểm trên AC, K là 1 điểm trên BE sao cho AI=EK Chưng minh 3 điểm I,M,K thẳng hàng.

c, Từ E kẻ [TEX]EH\perp BC(H\in BC)[/TEX]. Biết [TEX]\widehat{HBE}=50^o;\widehat{MEB}=25^o[/TEX]. Tính [TEX]\widehat{HEM}[/TEX] và [TEX]\widehat{MEB}[/TEX]

a. Xét hai tam giác [TEX]AMC[/TEX] và [TEX]BME[/TEX],
+ [TEX]AM=ME[/TEX] (gt)
+ [TEX]\widehat{BME}= \widehat{AMC}[/TEX] (hai góc đối đỉnh)
+ [TEX]BM=MC[/TEX] (gt)

[TEX]\Rightarrow \bigtriangleup AMC= \bigtriangleup EMB[/TEX] (c.g.c)
[TEX]\Rightarrow EB=AC[/TEX] (hai cạnh tương ứng)

Cũng từ [TEX]\bigtriangleup AMC= \bigtriangleup EMB \Rightarrow \widehat{ACM}= \widehat{EBM} \Rightarrow EB // AC[/TEX] (hai góc so le trong bằng nhau)