G
giangln.thanglong11a6
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Dưới đây là 1 số đề ôn tập Toán HK I:
Bài 1: Cho hàm số [TEX]y=x^4+mx^2-m-1[/TEX] có đồ thị [TEX](C_m)[/TEX]
a) Khảo sát và vẽ đồ thị hàm số với m=-1. Từ đó biện luận theo tham số k số nghiệm của PT [TEX]4x^2(1-x^2)=k[/TEX]
b) Chứng minh rằng [TEX](C_m)[/TEX] luôn đi qua điểm A cố định khi m thay đổi. Tìm m để tiếp tuyến của [TEX](C_m)[/TEX] tại A song song với đường thẳng (d):y=2x.
Bài 2:
a) Với giá trị nào của m thì PT sau có 4 nghiệm phân biệt:
[TEX](\frac{1}{5})^{\left|x^2-4x+3 \right|}=m^4-m^2+1[/TEX]
b) GPT: [TEX]log_{3-2x}(2x^2-9x+9)+log_{3-x}(4x^2-12+9)-4=0[/TEX]
Bài 3:
a) Tìm[TEX] \lim_{x\rightarrow 0} \frac{e^x-e^{-x}-2x}{2x-sinx}[/TEX]
b) Tìm GTNN của hàm số:
[TEX]y=(2+\sqrt{3})^{2x}+(2-\sqrt{3})^{2x}-8[(2+\sqrt{3})^{x}+(2-\sqrt{3})^{x}][/TEX]
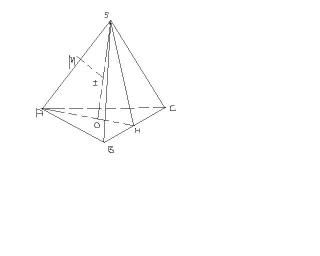
Bài 4: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc tại đỉnh của mỗi mặt bên bằng [TEX]2\alpha[/TEX].
a) Xác định tâm và tính bán kính, diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD theo a và [TEX]\alpha[/TEX].
b) Xác định tâm và tính bán kính của mặt cầu nội tiếp S.ABCD theo a và [TEX]\alpha[/TEX]. Tính thể tích của khối cầu nội tiếp S.ABCD.
c) Tính a và [TEX]\alpha[/TEX] để tâm mặt cầu ngoại tiếp và nội tiếp S.ABCD trùng nhau.
Bài 5: Cho a+b+c=1. CMR [TEX]\frac{1}{3^a}+\frac{1}{3^b}+\frac{1}{3^c} \geq 3(\frac{a}{3^a}+\frac{b}{3^b}+\frac{c}{3^c})[/TEX]
Đề số 1
Bài 1: Cho hàm số [TEX]y=x^4+mx^2-m-1[/TEX] có đồ thị [TEX](C_m)[/TEX]
a) Khảo sát và vẽ đồ thị hàm số với m=-1. Từ đó biện luận theo tham số k số nghiệm của PT [TEX]4x^2(1-x^2)=k[/TEX]
b) Chứng minh rằng [TEX](C_m)[/TEX] luôn đi qua điểm A cố định khi m thay đổi. Tìm m để tiếp tuyến của [TEX](C_m)[/TEX] tại A song song với đường thẳng (d):y=2x.
PHP:
Đã có lời giải.a) Với giá trị nào của m thì PT sau có 4 nghiệm phân biệt:
[TEX](\frac{1}{5})^{\left|x^2-4x+3 \right|}=m^4-m^2+1[/TEX]
Đã có lời giải ở đây
b) GPT: [TEX]log_{3-2x}(2x^2-9x+9)+log_{3-x}(4x^2-12+9)-4=0[/TEX]
PHP:
Đã có lời giải.a) Tìm[TEX] \lim_{x\rightarrow 0} \frac{e^x-e^{-x}-2x}{2x-sinx}[/TEX]
PHP:
Đã có lời giải.[TEX]y=(2+\sqrt{3})^{2x}+(2-\sqrt{3})^{2x}-8[(2+\sqrt{3})^{x}+(2-\sqrt{3})^{x}][/TEX]
PHP:
Đã có lời giải.a) Xác định tâm và tính bán kính, diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD theo a và [TEX]\alpha[/TEX].
b) Xác định tâm và tính bán kính của mặt cầu nội tiếp S.ABCD theo a và [TEX]\alpha[/TEX]. Tính thể tích của khối cầu nội tiếp S.ABCD.
c) Tính a và [TEX]\alpha[/TEX] để tâm mặt cầu ngoại tiếp và nội tiếp S.ABCD trùng nhau.
Bài 5: Cho a+b+c=1. CMR [TEX]\frac{1}{3^a}+\frac{1}{3^b}+\frac{1}{3^c} \geq 3(\frac{a}{3^a}+\frac{b}{3^b}+\frac{c}{3^c})[/TEX]
PHP:
Đã có lời giải.
Last edited by a moderator: