[Toán 12]-1 số bài logarit- hàm số mũ

[yenngocthu]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

[TEX]1, x.2^x=x(3-x)+2(2^x-1)[/TEX]

[TEX]2,x^{log_29}=x^2.3^{log_2x}-x^{log_23}[/TEX]

[TEX]3,sin^2 x.2^{cos2x}+\frac12sin^22x+cos2x=1[/TEX]

[TEX]4,(26+15\sqrt3)^x+2(7+4\sqrt3)^x-2(2-\sqrt3)^x=1[/TEX]

[TEX]GPT{(\sqrt{3}+1)}^{x}+{(\sqrt{3}-1)}^{x}={2}^{x}[/TEX]trang 1

Tiếp theo là 1 BĐT logarit đơn giản :

CMR [TEX]{log}_{2}3>{log}_{3}4[/TEX]

Tr.1

À quên tranh thủ post bài kiểm tra của mình lên luôn:
GPT [TEX]{2}^{cosx}+cosx.{3}^{x}=1[/TEX]
GPT [TEX]{3}^{sinx}+sinx.{2}^{x-1}=1[/TEX]
[TEX](1+cosx)(2+{4}^{cosx})=3.{4}^{cosx}[/TEX]

Tr.2[/QUOTE]

giải bất pt
[TEX]1.log_m(2x^2+x+3)\ge log_m(3x^2-x)[/TEX]biết x=1 là 1 nghiệm của pt trên .
[TEX]2.log_{x\sqrt3}(5x^2-18x+16}>2[/TEX]
[TEX]3.log_x(x-\frac14)\ge2[/TEX]Tr.2

thử làm mấy bài nha :
bài 1:
từ cái bài của @giangln.thanglong chúng ta có thể đưa ra bài toán tổng quát sau :
[tex] log_{n-1}n > log_{n}(n+1)[/tex].
bài 2 : giải pt
[tex]log_{7}x= log_{3}(\sqrt{x}+2)[/tex]
bài 3 : giải pt
[tex]log_5(\sqrt{x-2\sqrt{x-1}} + \sqrt {x+3-4\sqrt{x-1}}) = 5^{\sqrt{x-2\sqrt{x-1}} + \sqrt {x+3-4\sqrt{x-1}}[/tex]
bài 4 : giải pt
[tex]\frac{3}{2}log_{\frac{1}{4}}(x+2)^2 -3 = log_{\frac{1}{4}}(4-x)^3 + log_{\frac{1}{4}}(x+6)^3[/tex] ..
Tr.3

Giải phương trình :
[TeX]1, log_5x=log_3(x-x^{log_52})[/TeX]
2, Giải phương trình
[TeX]\large\log_7\(\cos\frac{x}{2}+3\text{tg}x-\frac{3\sqrt{3}}{2}\)+\log_{\frac{1}{7}}\(cos (\frac{x}{2})+\text{tg}2x-\frac{3\sqrt{3}}{2}\)=0[/TeX]
3,[TeX]\large 3\log_{2}^{2}\sin{x}+\log_2(1-\cos{2x})=2[/TeX]
4,[TeX]\large\frac{1}{4}+\log_2(\cos{x}).\log_2(2\cos{x})=\log_3(\text{tg}x).\log_2(2\cos^2{x})[/TeX]
5,[TeX]\large\frac{\log_2(2\sin{x})-\frac{1}{2}\log_2{3}}{\log_3(6+3\cos{2x})+\log_3{2}}=1[/TeX]
6,[TeX]\large (\log_3(2\cos{x}))^{\sin{x}-1}=\frac{1}{\sqrt{2}}[/TeX]
7,[TeX]\large\frac{2}{3}.3^{\log_6\text{tg}^2x}+\frac{3}{2}.2^{\log_6\text{tg}^2x}=6(3-\text{cotg}^{2}x)[/TeX]Tr.3

a, [tex]25^(1+2x-x^2)+9^(1+2x-x^2)>=34.5^(2x-x^2)[/tex]
b,[tex]7^(6-x)=x+2[/tex]
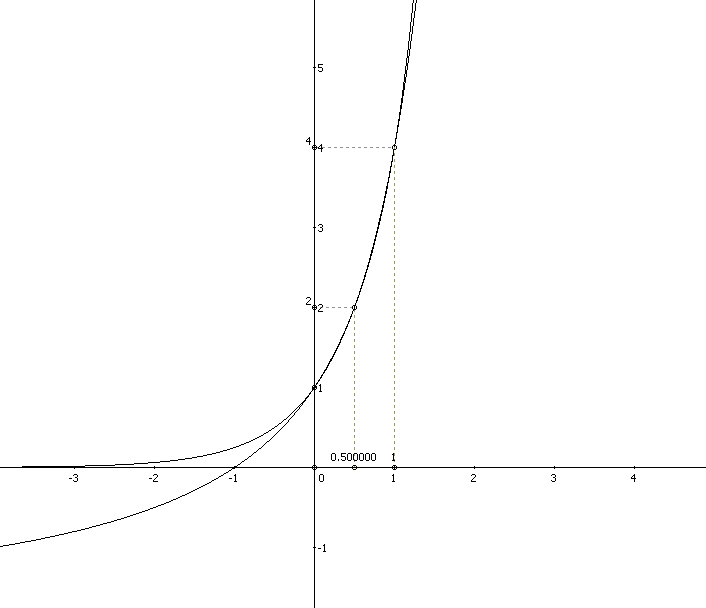
c,[tex]2^x=3^(x/2)+1[/tex]
d,[tex]\sqrt{-3x^2-5x+2}+2x>3^x.2x.\sqrt{-3x^2-5x+2} [/tex]Tr.4

thêm bài nữa nè : giải Pt
[tex]\sqrt{5^x-2x}- \sqrt{2x+1}= 1+4x+4x.5^x+5^{2x}[/tex]
Tr.4

tìm x biết
[TEX](x-1)^{3x-1}=x-1[/TEX]
cẩn thận kẻo nhầm)............................Tr.5

Không dùng logarit hãy CMR: [tex]2^3^{100} < 3^2^{100}[/tex]Tr.5

có mấy bài mới đây
[TEX]log_2(x-\sqrt{x^2-1}).log_3(x+\sqrt{x^2-1})=log_6(x+\sqrt{x^2-1})[/TEX]Tr.5

1,[TEX]log_2log_3log_4x=log_4log_3log_2x[/TEX]

2,[TEX]log_2log_3x+log_3log_2x=log_3log_3x[/TEX]Tr.6

trời có mấy ngày mà topic này chìm quá đi
thêm mấy bào nữa rùi chuyểnn sang tích phân
[TEX]1,x^{lg^2x^2-3lgx-4,5}=10^{-2lgx}[/TEX]

[TEX]2,5^{lgx}=50-x^{lg5}[/TEX]

[TEX]3,2^{log_5(x+3)=x[/TEX]Tr.7

Mọi người giải thử bài này xem : CMR với n>=0 thì
[tex]log_2(1+2^n)>log_3(3^n+\sqrt{2^n})[/tex]Tr.7

góp bài cho xôm ( chả bit có chưa )
Tìm nghiệm (x,y) từ pt:
[tex]8^{sin^2x} + 8^{cos^2x} = 10 + cos2y[/tex]Tr.8

giai jum toi bai ne cai':tim m để pt sau có 2n trái dấu
pt: [tex]m4^x - (2m + 1)2^x + m +4 = 0 [/tex]

Tìm m để PT sau có nghiệm duy nhất:

[tex]\frac{lg{(mx)}}{lg{(x+1)}} = 2[/tex]

Giải chi tiết hộ tớ nhá các bạn ! Thanks !

Tr.8

hôm trước đọc trong 1 quyển sách có 1 bài logarit cũng hay post lên cho mọi ngưòi giải thử nha
[TEX]log_2^{2x}+log_2\frac x4=5log_x8+25(log_x2)^2[/TEX]Tr.10

 

[boyxuthanh]

bài 2
[tex](x^log_23)^2=x^2*3^{log_2x}-x^log_23[/tex]
đặt [tex]x^log_23=t[/tex] đk t>0
=> [tex]t^2=x^2*t - t[/tex]
=> [tex]t=x^2 - 1[/tex]
=>[tex]x^log_23=x^2 - 1[/tex]
=>[tex]log_2x*log_23=log_2(x^2 - 1)[/tex]
=>[tex]log_2x=log_3(x^2-1)[/tex]
đặt [tex]log_2x=t[/tex] => x=2^t
=> [tex]t=log_3(2^2t - 1)[/tex]
=> [tex]4^t=3^t + 1[/tex]
[tex]log_2x=1=>x=2[/tex]
nếu gõ công thức mà ko đc mong mod sữa giúp mình nha

 

[potter.2008]

tớ làm thử mấy bài : hì

[TEX]1, x.2^x=x(3-x)+2(2^x-1)[/TEX]

[tex]\Leftrightarrow 2^x(x-2)=-x^2+3x-2[/tex]..ok..

[TEX]2,x^{log_29}=x^2.3^{log_2x}-x^{log_23}[/TEX]

[TEX]3,sin^2 x.2^{cos2x}+\frac12sin^22x+cos2x=1[/TEX]
Bài này tớ nhường mọi người đó , nếu ko được tớ sẽ giải....ngại gõ ct lắm rùi..
[TEX]4,(26+15\sqrt3)^x+2(7+4\sqrt3)^x-2(2-\sqrt3)^x=1[/TEX][/QUOTE]

[tex]\Leftrightarrow (2+\sqrt3)^{3x}+2(2+\sqrt3)^{2x}-2(\frac{1}{2+\sqrt3)}^x=1[/TEX]
đặt [tex]{2+\sqrt3}^x=a[/tex]
pt [tex]\Leftrightarrow {a}^4+2a^3-a-2=0[/tex] cái này nhóm là xong lun..

 

[yenngocthu]

bài 2

cách 2 của bài 2 nè các pác
[TEX]a^{log_bc}=c^{log_ba}[COLOR="Blue"][/COLOR][/TEX]
áp dụng có [TEX]x^{log_29}=9^{log_2x}[/TEX]
[TEX]x^{log_23}=3^{log_2x}[/TEX]
pt ban đầu trở thành
[TEX]9^{log_2x}=x^2.3^{log_2x}-3^{log_2x}\Leftrightarrow(3^{log_2x})^2=(x^2-1).3^{log_2x}(1)[/TEX]
[TEX]do3^{log_2x}>0[/TEX]nên
[TEX](1)<=>3^{log_2x}=x^2-1(2)[/TEX]
đặt[TEX]y=log_2x<=>x=2^y[/TEX]có (2) trở thành
[TEX]x^2-1=2^{2y}-1[/TEX]
vậy[TEX]3^y=2^{2y}-1[/TEX]
đến đay dùng tính chất hàm nghịch biến là ra

 

[giangln.thanglong11a6]

Bài 3)
Biến đổi [TEX]1- cos2x-\frac{1}{2}{sin}^{2}2x=2{sin}^{4}x[/TEX]
PT [TEX]\Leftrightarrow sinx=0\Leftrightarrow x=k\pi [/TEX]
hoặc [TEX]{2}^{cos2x}=2{sin}^{2}x[/TEX]
Đặt [TEX]2{sin}^{2}x=t\geq 0[/TEX]
PT [TEX]\Leftrightarrow {2}^{1-t}=t [/TEX]
Nếu t>1 thì VT<1<VP
Nếu t<1 thì VT>1>VP
t=1 thoả mãn[TEX]\Leftrightarrow {sin}^{2}x=\frac{1}{2}\Leftrightarrow x=\frac{\pi }{4}+\frac{k\pi}{2} [/TEX]

 

[giangln.thanglong11a6]

Để góp vui với Yến tớ cũng cho thêm 1 bài nho nhỏ:
[TEX]GPT{(\sqrt{3}+1)}^{x}+{(\sqrt{3}-1)}^{x}={2}^{x}[/TEX]

 

[nguyenminh44]

Bài này nếu để ý thấy [TEX](\sqrt{3}+1)(\sqrt{3}-1)=2[/TEX] rồi tiếp tục đi theo hướng đó thì chắc đến....mới giải ra.

Nếu x> 0 thì ta có [TEX](\sqrt{3}+1)^x > 2^x[/TEX] và [TEX](\sqrt{3}-1)^x>0 \Rightarrow[/TEX] VT>VP

Tương tự cho trường hợp x<0

Phương trình vô nghiệm

 

[giangln.thanglong11a6]

Tiếp theo là 1 BĐT logarit đơn giản :

CMR [TEX]{log}_{2}3>{log}_{3}4[/TEX]

Cố gắng chỉ dùng biến đổi tương đương nhé, dùng hàm số dài lắm.

 

[potter.2008]

Tiếp theo là 1 BĐT logarit đơn giản :

CMR [TEX]{log}_{2}3>{log}_{3}4[/TEX]

Cố gắng chỉ dùng biến đổi tương đương nhé, dùng hàm số dài lắm.

bài này tớ làm thế này nè : hơi thủ công chút : ...định làm cách khác mà ngại rùi :
[TEX]{log}_{2}3>{log}_{3}4[/TEX]
[tex]\Leftrightarrow {log_{2}3}^2={log}_{2}4=2[/tex]
hì cái cách này ko hay lắm nhưng mà nhanh
[tex]log_{2}3=\frac{log3}{log2}[/tex]..tính máy tính cho gọn

 

[potter.2008]

thử làm mấy bài nha :
bài 1:
từ cái bài của @giangln.thanglong chúng ta có thể đưa ra bài toán tổng quát sau :
[tex] log_{n-1}n > log_{n}(n+1)[/tex].
bài 2 : giải pt
[tex]log_{7}x= log_{3}(\sqrt{x}+2)[/tex]
bài 3 : giải pt
[tex]log_5(\sqrt{x-2\sqrt{x-1}} + \sqrt {x+3-4\sqrt{x-1}}) = 5^{\sqrt{x-2\sqrt{x-1}} + \sqrt {x+3-4\sqrt{x-1}}[/tex]
bài 4 : giải pt
[tex]\frac{3}{2}log_{\frac{1}{4}}(x+2)^2 -3 = log_{\frac{1}{4}}(4-x)^3 + log_{\frac{1}{4}}(x+6)^3[/tex] ..
làm tạm thế đã nha

sorry @marymary nha ..hôm trước đang bận nên post nhầm ....

 

[giangln.thanglong11a6]

bài này tớ làm thế này nè : hơi thủ công chút : ...định làm cách khác mà ngại rùi :
[TEX]{log}_{2}3>{log}_{3}4[/TEX]
[tex]\Leftrightarrow {log_{2}3}^2={log}_{2}4=2[/tex]
hì cái cách này ko hay lắm nhưng mà nhanh
[tex]log_{2}3=\frac{log3}{log2}[/tex]..tính máy tính cho gọn

Anh ơi viết lại cho rõ : [TEX]{log}_{2}3>{log}_{3}4[/TEX]

[TEX]\Leftrightarrow {log}_{2}3.{log}_{2}3>{log}_{2}3.{log}_{3}4[/TEX]

[TEX]\Leftrightarrow ({log}_{2}3)^2>{log}_{2}4=2[/TEX]

Do [TEX]({log}_{2}3)^2>({log}_{2}2\sqrt{2})^2=(3/2)^2>2[/TEX] nên suy ra đpcm.

@potter.2008: Anh ơi mấy bài của Phạm Kim Hùng em xem gần hết rồi post làm gì. Mà đây là mục logarit chứ có phải Đại số đâu?

 

[hunter_dk]

CMR [TEX]{log}_{2}3>{log}_{3}4[/TEX]

Cho tớ tham gia zới nào
Tớ giải thế này không biết có đúng không:

Giả sử : [TEX]{log}_{2}3>{log}_{3}4[/TEX]
<=> [TEX]{log}_{4}3/{log}_{4}2>{log}_{3}4[/TEX]
<=> [TEX]{log}_{4}3/{log}_{3}4>{log}_{4}2[/TEX]
<=> [TEX]1/2{log}_{2}2<1[/TEX]
<=> 1/2 < 1 (cái này chắc luôn đúng hen )

===> dpcm

 

[giangln.thanglong11a6]

Ôg hunter sai rồi. [TEX]\frac{{log}_{4}3}{{log}_{3}4}={({log}_{4}3)}_{2}[/TEX]
Nhớ nhầm công thức là toi đấy.

À quên tranh thủ post bài kiểm tra của mình lên luôn:
GPT [TEX]{2}^{cosx}+cosx.{3}^{x}=1[/TEX]
GPT [TEX]{3}^{sinx}+sinx.{2}^{x-1}=1[/TEX]

 

[chuotnhatk48]

[TEX]log_2(3)[/TEX] = 1 / [TEX]log_3(2)[/TEX]
\Rightarrow [TEX]log_2(3)[/TEX] > [TEX]log_3(4)[/TEX] \Leftrightarrow 1> [TEX]log_3(2)[/TEX] x [TEX]log_3(4)[/TEX]
mà ta có [TEX]log_3(2)[/TEX] + [TEX]log_3(4)[/TEX] = [TEX]log_3(8)[/TEX] < [TEX]log_3(9)[/TEX] = 2
\Rightarrow [TEX]log_3(2)[/TEX] x [TEX]log_3(4)[/TEX] < (( [TEX]log_3(2)[/TEX] + [TEX]log_3(4)[/TEX] )^2 ) /4 =1 \Rightarrow điều phải CM
mọi người coi xem làm như vậy có đc ko.
giải cho mình bài này luôn : CMR
[TEX]\frac{x}{sqrt{x^2 +8yz}}[/TEX] \geq [TEX]\frac{x^{\frac{4}{3}}}{x^{\frac{4}{3}} +y^{\frac{4}{3}} + z^{\frac{4}{3}}}[/TEX]

 

[giangln.thanglong11a6]

Bạn Chuột dùng BĐT AM-GM (Cauchy) ấy mà. Cũng được, nhưng ở lớp mà cứ dùng mấy thứ đó sợ các thầy không hiểu đâu.
@chuotnhatk48:Cái bài đó lời giải có đầy trong STK ấy mà, bình phương mà dùng AM-GM thôi.

Mới lượm được PT mũ hay phết :

[TEX](1+cosx)(2+{4}^{cosx})=3.{4}^{cosx}[/TEX]

 

[potter.2008]

Bạn Chuột dùng BĐT AM-GM (Cauchy) ấy mà. Cũng được, nhưng ở lớp mà cứ dùng mấy thứ đó sợ các thầy không hiểu đâu.
@chuotnhatk48:Cái bài đó lời giải có đầy trong STK ấy mà, bình phương mà dùng AM-GM thôi.

Mới lượm được PT mũ hay phết :

[TEX](1+cosx)(2+{4}^{cosx})=3.{4}^{cosx}[/TEX]

thử giải thế này nha : bận quá ...
cái này chuyển về :
[tex]\frac{2+2cosx}{2-cosx} = 4^{cosx}[/tex]
Dùng đồ thị hàm số ..có nghiệm duy nhất là cosx= 1 ..ok..

 

[giangln.thanglong11a6]

thử giải thế này nha : bận quá ...
cái này chuyển về :
[tex]\frac{2+2cosx}{2-cosx} = 4^{cosx}[/tex]
Dùng đồ thị hàm số ..có nghiệm duy nhất là cosx= 1 ..ok..

Anh ơi sai mất rồi. Đáp án là [TEX]cosx={{0; \frac{1}{2}; 1}}[/TEX] mà. Nếu bài này dễ thế thì còn gì đáng nói nữa.

 

[potter.2008]

vội quá nên có chút nhầm lẫn ..hì hì..
các bạn thử coi sao

 

[marymary]

các bạn post nhầm chủ đề rùi đấy
nhất là bạn potter, bạn là mod mà cũng o hiểu cái này sao
nhan tiện mình cũng xin tặng các bạn 1 số bài toán về logarit
giải bất pt
[TEX]1.log_m(2x^2+x+3)\ge log_m(3x^2-x)[/TEX]biết x=1 là 1 nghiệm của pt trên .
[TEX]2.log_{x\sqrt3}(5x^2-18x+16}>2[/TEX]
[TEX]3.log_x(x-\frac14)\ge2[/TEX]

 

[giangln.thanglong11a6]

Bài 2: [TEX]{log}_{x\sqrt{3}}(5{x}^{2}-18x+16)>2[/TEX]

ĐK:[TEX] x\epsilon (0;\frac{\sqrt{3}}{3})\bigcup (\frac{\sqrt{3}}{3};\frac{8}{5})\bigcup (2;+\infty)[/TEX]

Xét 2 TH:

-TH1: [TEX]x>\frac{\sqrt{3}}{3}[/TEX]

BPT [TEX]\Leftrightarrow 5{x}^{2}-18x+16>{(x\sqrt{3})}^{2}=3{x}^{2}[/TEX]

[TEX]\Leftrightarrow {x}^{2}-9x+8>0[/TEX]

[TEX]\Leftrightarrow x>8[/TEX] hoặc [TEX]x<1[/TEX]

Từ ĐK ta thu được [TEX]x\epsilon (\frac{\sqrt{3}}{3};1)\bigcup(8;+\infty)[/TEX]

-TH2: [TEX]x<\frac{\sqrt{3}}{3}[/TEX]

BPT [TEX]\Leftrightarrow 5{x}^{2}-18x+16<{(x\sqrt{3})}^{2}=3{x}^{2}[/TEX]

[TEX]\Leftrightarrow 1<x<8[/TEX] không thoả mãn ĐK.

Bài 3: ĐK [TEX]x\epsilon (\frac{1}{4};1)\bigcup (1;+\infty)[/TEX]
Xét 2 TH:
-TH1: x>1: BPT [TEX]\Leftrightarrow x-\frac{1}{4}\geq{x}^{2}[/TEX]

[TEX]\Leftrightarrow {(x-\frac{1}{2})}^{2}\leq0[/TEX]

[TEX]\Leftrightarrow x=\frac{1}{2}[/TEX] loại.

-TH2: x<1 : BPT [TEX]\Leftrightarrow x-\frac{1}{4}\leq{x}^{2}[/TEX]

[TEX]\Leftrightarrow {(x-\frac{1}{2})}^{2}\geq0[/TEX] hiển nhiên đúng.

Vậy BPT có nghiệm 1/4<x<1.