Toán 10 [Toán 10]Bất phương trình

[bigbang195]

Giải PT:

 

[tell_me_goobye]

Giải PT:

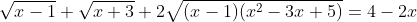
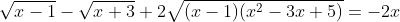
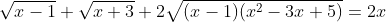
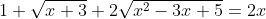
đặt [TEX]\sqrt{x-1}+\sqrt{x+3} =a [/TEX]
=> [TEX] a^2 = 2x+2+2\sqrt{(x-1)(x+3)}[/TEX]
đến đây ok rùi
x=1

 

[tell_me_goobye]

[TEX]1)\sqrt{1+\sqrt{(1-x^2}}. \sqrt{ (1-x)^3 - \sqrt{(1+x)^3}}=2+\sqrt{1-x^2}[/TEX]
[TEX]2, 64x^6-112x^4+56x^2-7=2\sqrt{1-x^2}[/TEX]
[TEX]3,\sqrt{(1-x)}-2x.\sqrt{(1-x^2)}-2x^2+1=0[/TEX]
[TEX]4,\sqrt{x-1}=-x^3-4x+5[/TEX]
[TEX]5,\sqrt{x-1}=-x^2+x+3[/TEX]
[TEX]6,\sqrt{x}=-x^3+2x^2-2x+1[/TEX]
[TEX]7,\sqrt{x-\sqrt{x^2-1}}+\sqrt{x+\sqrt{x^2-1}}=2[/TEX]
[TEX]8,2\sqrt{x+2\sqrt{x-1}}-\sqrt{x-2\sqrt{x-1}}=x+3[/TEX]

 

[vuanoidoi]

[TEX]8,2\sqrt{x+2\sqrt{x-1}}-\sqrt{x-2\sqrt{x-1}}=x+3[/TEX]

thấy dạo này ế ẩm quá mình mở màn làm 1 bài mong các bạn chém nhiệt tình
[tex]<=>2\sqrt{x-1+2\sqrt{x-1}+1}-\sqrt{x-1-2\sqrt{x-1}+1}=x+3[/TEX]
[tex]<=>2\sqrt{(\sqrt{x-1}+1)^2}-\sqrt{(\sqrt{x-1}-1)^2}=x+3[/TEX]
$$<=>2(\sqrt{x-1}+1)-|\sqrt{x-1}-1|=x+3$$
$$<=>2\sqrt{x-1}-|\sqrt{x-1}-1|=x+1$$

 

[vuanoidoi]

tiếp

[TEX] 1) \sqrt{1+\sqrt{2x-x^2}} +\sqrt{1-\sqrt{2x-x^2}}= 2(x-1)^4(2x^2-4x+1) [/TEX]

đk:$$0 \leq x \leq2$$
bình phương vế rồi đặt:$$|x-1|=a \geq 0$$
rồi đánh giá a=1 là nghiệm của PT
=>x=2

 

[vuanoidoi]

[TEX]5,\sqrt{x-1}=-x^2+x+3[/TEX]

[tex]<=> \sqrt{x-1}-1=-x^2+x+2[/TEX]
$$<=> \sqrt{x-1}-1=(2-x)(x+1)$$
$$<=>\frac{(\sqrt{x-1}-1)(\sqrt{x-1}+1)}{\sqrt{x-1}+1} =(2-x)(x+1)$$
$$<=>\frac{x-2}{\sqrt{x-1}+1} =(2-x)(x+1)$$
o=>

 

[bigbang195]

đk:$$0 \leq x \leq2$$
bình phương vế rồi đặt:$$|x-1|=a \geq 0$$
rồi đánh giá a=1 là nghiệm của PT
=>x=2

Còn 1 nghiệm là [TEX]x=0[/TEX] , cậu có thể làm tiếp bài này không :khi (96)::khi (96):,

cảm ơn ==!

 

[0915549009]

[TEX]7,\sqrt{x-\sqrt{x^2-1}}+\sqrt{x+\sqrt{x^2-1}}=2[/TEX]

[TEX]\sqrt{x-\sqrt{x^2-1}}+\sqrt{x+\sqrt{x^2-1}}=2 \Leftrightarrow 2x + 2\sqrt{x^2-(\sqrt{x^2-1})^2}=4[/TEX]
[TEX]\Leftrightarrow2x+2(x^2-x^2+1)=4\Leftrightarrow2x=2\Leftrightarrow x=1[/TEX]
:khi (54)::khi (54)::khi (54):

 

[tell_me_goobye]

sao dạo này không ai vào làm vậy ?
chán ế =======================

 

[tell_me_goobye]

tiếp

[TEX] 1) \sqrt{1+\sqrt{2x-x^2}} +\sqrt{1-\sqrt{2x-x^2}}= 2(x-1)^4(2x^2-4x+1) [/TEX]
[TEX] 2) 3x (2+\sqrt{9x^2+3})+(4x+2)\sqrt{1+\sqrt{1+x+x^2}}=0[/TEX]

mình gợi ý bài này dùng hàm số nhá
============================================

 

[lamtrang0708]

 

[tell_me_goobye]

chú ý
[TEX] 12x-8 =2[(2x+4)-4(2-x)]=2[(\sqrt{2x+4})^2-(2\sqrt{2-x})^2] [/TEX]

BPT trở thành
[TEX] (\sqrt{2x+4}-2\sqrt{2-x})(2\sqrt{2x+4}+4\sqrt{2-x}-\sqrt{9x^2+16}) >0 [/TEX]
[TEX] \Leftrightarrow \left[\begin{\sqrt{2x+4}-2\sqrt{2-x}>0}\\{2\sqrt{2x+4}+4\sqrt{2-x}>\sqrt{9x^2+16} [/TEX]
hoặc
[TEX] \left[\begin{\sqrt{2x+4}-2\sqrt{2-x}<0}\\{2\sqrt{2x+4}+4\sqrt{2-x}<\sqrt{9x^2+16}[/TEX]
đến đây đơN giản hơn nhiều

 

[legendismine]

[TEX]\frac {3-2\sqrt {x^2+3x+2}}{1-2\sqrt {x^2-x+1}}>1[/TEX]
ai giai nao di nao`

 

[duynhan1]

[TEX]\frac {3-2\sqrt {x^2+3x+2}}{1-2\sqrt {x^2-x+1}}>1[/TEX]
ai giai nao di nao`

[TEX]DK : \left{ x \le - 2 \\ x \ge - 1[/TEX]

Nhận xét : [TEX] 1-2\sqrt {x^2-x+1} \le 1 - 2\sqrt{\frac34} < 0 [/TEX]

Mẫu luôn bé hơn 0 nên bpt tương đương với :

[TEX]3-2\sqrt {x^2+3x+2} <1-2\sqrt {x^2-x+1} [/TEX]

[TEX]\Leftrightarrow \sqrt{x^2 + 3x+ 2}> \sqrt{x^2-x+1} + 1 [/TEX]

[TEX]\Leftrightarrow x^2 + 3x + 2 > x^2 - x + 2 + 2 \sqrt{x^2-x+1} [/TEX]

[TEX]\Leftrightarrow 2x > \sqrt{x^2-x+1} [/TEX]

[TEX]\Leftrightarrow \left{ x > 0 \\ 4x ^2 > 3x ^2 - x + 1 [/TEX]

[TEX]\Leftrightarrow \left{ x > 0 \\ x ^2+x - 1 > 0[/TEX]

............

 

[legendismine]

[TEX]DK : \left{ x \le - 2 \\ x \ge - 1[/TEX]

Nhận xét : [TEX] 1-2\sqrt {x^2-x+1} \le 1 - 2\sqrt{\frac34} < 0 [/TEX]

Mẫu luôn bé hơn 0 nên bpt tương đương với :

[TEX]3-2\sqrt {x^2+3x+2} <1-2\sqrt {x^2-x+1} [/TEX]

[TEX]\Leftrightarrow \sqrt{x^2 + 3x+ 2}> \sqrt{x^2-x+1} + 1 [/TEX]

[TEX]\Leftrightarrow x^2 + 3x + 2 > x^2 - x + 2 + 2 \sqrt{x^2-x+1} [/TEX]

[TEX]\Leftrightarrow 2x > \sqrt{x^2-x+1} [/TEX]

[TEX]\Leftrightarrow \left{ x > 0 \\ 4x ^2 > 3x ^2 - x + 1 [/TEX]

[TEX]\Leftrightarrow \left{ x > 0 \\ x ^2+x - 1 > 0[/TEX]

............

Sai mat rồi anh ơi:| đáp số là[TEX](-\infty,-2)U(\frac {\sqrt{13}-1}{6},+\infty)[/TEX]

 

[protankhai]

mình cũng mạo muội xin post 1 bài
a) $$\sqrt{1-4x} - 9 = 3x$$
b) $$x^2 + \sqrt{x^2 - x} - 9 = x+3$$

 

[matnatinhyeu_1995]

mình cũng mạo muội xin post 1 bài
a) $$\sqrt{1-4x} - 9 = 3x$$
b) $$x^2 + \sqrt{x^2 - x} - 9 = x+3$$

a)<=>$$\left\{ \begin{array}{l} x\geq-3 \\ 1-4x=9x^2+54x+81 \end{array} \right.$$
<=>$$\left\{ \begin{array}{l} x\geq-3 \\ x=-2 ; x=-40/9 \end{array} \right.$$
<=>x=-2
b)đk:[tex]\left[\begin{x\geq1}\\{x\leq0} [/tex]
pt<=>$$x^2-x+\sqrt{x^2-x}+1/4=49/4$$
<=>$$(\sqrt{x^2-x}+1/2)^2=49/4$$
<=>$$\sqrt{x^2-x}=3$$(còn 1 TH nữa nhưng loại vì VT\geq0)
<=>$$x^2-x=9$$
bạn tự giải tiếp pt này nhé.nghiệm lẻ nên tớ lười viết tiếp.

 

[matnatinhyeu_1995]

[TEX]x \leq \frac{1}4[/TEX]................................................................................

chỗ đó do tớ viết chữ hoặc nhưng chẳng hiểu sao nó lại thành vậy nữa.
còn phần điều kiện theo như tớ dc học thì
$$\sqrt{g(x)}=h(x)$$
$$\Leftrightarrow \left\{ \begin{array}{l} h(x)\geq0 \\ g(x)=h(x)^2 \end{array} \right.$$

 

[nhockthongay_girlkute]

[TEX]\sqrt{7x+7}+\sqrt{7x-6}+2\sqrt{49x^2-7x-42}<181-14x[/TEX]

 

[heyday195]

Đạt 1 cái căn là a 1 cái b
\Leftrightarrow (a+b)^2-(a+b)-179<0 .Xong
a^2 - b^2 =13